Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T09:18:58.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear unsteady streaks engendered by the interaction of free-stream vorticity with a compressible boundary layer

Published online by Cambridge University Press:  15 March 2017

Elena Marensi Open the ORCID record for Elena Marensi [Opens in a new window] ,
Pierre Ricco  and
Xuesong Wu Open the ORCID record for Xuesong Wu [Opens in a new window]
Elena Marensi*
Affiliation:
Department of Mechanical Engineering, The University of Sheffield, S1 3JD Sheffield, UK Department of Fluid Dynamics, A*Star Institute of High Performance Computing, 138632 Singapore
Pierre Ricco
Affiliation:
Department of Mechanical Engineering, The University of Sheffield, S1 3JD Sheffield, UK
Xuesong Wu
Affiliation:
Department of Mathematics, Imperial College London, SW7 2AZ London, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The nonlinear response of a compressible boundary layer to unsteady free-stream vortical fluctuations of the convected-gust type is investigated theoretically and numerically. The free-stream Mach number is assumed to be of 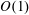$O(1)$ and the effects of compressibility, including aerodynamic heating and heat transfer at the wall, are taken into account. Attention is focused on low-frequency perturbations, which induce strong streamwise-elongated components of the boundary-layer disturbances, known as streaks or Klebanoff modes. The amplitude of the disturbances is intense enough for nonlinear interactions to occur within the boundary layer. The generation and nonlinear evolution of the streaks, which acquire an 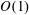$O(1)$ magnitude, are described on a self-consistent and first-principle basis using the mathematical framework of the nonlinear unsteady compressible boundary-region equations, which are derived herein for the first time. The free-stream flow is studied by including the boundary-layer displacement effect and the solution is matched asymptotically with the boundary-layer flow. The nonlinear interactions inside the boundary layer drive an unsteady two-dimensional flow of acoustic nature in the outer inviscid region through the displacement effect. A close analogy with the flow over a thin oscillating airfoil is exploited to find analytical solutions. This analogy has been widely employed to investigate steady flows over boundary layers, but is considered herein for the first time for unsteady boundary layers. In the subsonic regime the perturbation is felt from the plate in all directions, while at supersonic speeds the disturbance only propagates within the dihedron defined by the Mach line. Numerical computations are performed for carefully chosen parameters that characterize three practical applications: turbomachinery systems, supersonic flight conditions and wind tunnel experiments. The results show that nonlinearity plays a marked stabilizing role on the velocity and temperature streaks, and this is found to be the case for low-disturbance environments such as flight conditions. Increasing the free-stream Mach number inhibits the kinematic fluctuations but enhances the thermal streaks, relative to the free-stream velocity and temperature respectively, and the overall effect of nonlinearity becomes weaker. An abrupt deviation of the nonlinear solution from the linear one is observed in the case pertaining to a supersonic wind tunnel. Large-amplitude thermal streaks and the strong abrupt stabilizing effect of nonlinearity are two new features of supersonic flows. The present study provides an accurate signature of nonlinear streaks in compressible boundary layers, which is indispensable for the secondary instability analysis of unsteady streaky boundary-layer flows.

JFM classification

Compressible Flows: Compressible boundary layers Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 817 , 25 April 2017 , pp. 80 - 121
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions: Applied Mathematics Series, No. 55. National Bureau of Standards.Google Scholar
Anderson, J. D. Jr. 2006 Hypersonic and High-Temperature Gas Dynamics, 2nd edn. AIAA.CrossRefGoogle Scholar
Anderson, J. D. Jr. 2007 Fundamentals of Aerodynamics, 4th edn. McGraw-Hill.Google Scholar
Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.Google Scholar
Arnal, D. & Juillen, J. C.1978 Contribution expérimentale à l’étude de la reptivité d’une couche limite laminaire à la turbulence de l’écoulement général. CERT RT 1/5018 AYD – ONERA.Google Scholar
Beckwith, I. E. & Miller, C. G. III 1990 Aerothermodynamics and transition in high-speed wind tunnels at NASA Langley. Annu. Rev. Fluid Mech. 22 (1), 419–439.CrossRefGoogle Scholar
Brandt, L., Schlatter, P. & Henningson, D. S. 2004 Transition in boundary layers subject to free-stream turbulence. J. Fluid Mech. 517, 167–198.CrossRefGoogle Scholar
Brinkerhoff, J. R. & Yaras, M. I. 2015 Numerical investigation of transition in a boundary layer subjected to favourable and adverse streamwise pressure gradients and elevated free stream turbulence. J. Fluid Mech. 781, 52–86.Google Scholar
Camci, C. & Arts, T. 1990 An experimental convective heat transfer investigation around a film-cooled gas turbine blade. Trans. ASME J. Turbomach. 112 (3), 497–503.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Champion, K. S. W., Cole, A. E. & Kantor, A. J. 1985 Standard and reference atmospheres. In Handbook of Geophysics and the Space Environment, vol. 14. Air Force Geophysics Laboratory.Google Scholar
Chang, C.-L., Malik, M. R., Erlebacher, M. Y. & Hussaini, M. Y.1991 Compressible stability of growing boundary layers using parabolized stability equations. AIAA Paper 91-1636.Google Scholar
Chang, C.-L., Malik, M. R. & Hussaini, M. Y.1990 Effects of shock on the stability of hypersonic boundary layers. AIAA Paper 90-1448.CrossRefGoogle Scholar
Coleman, T. L. & Steiner, R.1960 Atmospheric turbulence measurements obtained from airplane operations at altitudes between 20 000 and 75 000 feet for several areas in the northern hemisphere. NASA Tech. Rep. NASA/TN D-548.Google Scholar
Cowley, S. J. & Hall, P. 1990 On the instability of hypersonic flow past a wedge. J. Fluid Mech. 214, 17–42.Google Scholar
Dong, M. & Wu, X. 2013 On continuous spectra of the Orr–Sommerfeld/Squire equations and entrainment of free-stream vortical disturbances. J. Fluid Mech. 732, 616–659.Google Scholar
Dongarra, J., Lumsdaine, A., Pozo, R. & Remington, K.2006 IML++ v. 1.2 Iterative Method Library. http://math.nist.gov/iml++/.Google Scholar
Dowell, E. H. 2014 A Modern Course in Aeroelasticity, vol. 217. Springer.Google Scholar
Dragos, L. 2004 Mathematical Methods in Aerodynamics. Springer.Google Scholar
Ehernberger, L. J. & Love, B. J.1975 High altitude gust acceleration environment as experienced by a supersonic airplane. NASA Tech. Rep. NASA/TN D-7868.Google Scholar
Farabee, T. M. & Casarella, M. J. 1991 Spectral features of wall pressure fluctuations beneath turbulent boundary layers. Phys. Fluids 3, 2410–2420.Google Scholar
Fedorov, A. V. & Khokhlov, A. P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14, 359–375.CrossRefGoogle Scholar
Fedorov, A. V. & Khokhlov, A. P. 2003 Receptivity of a high-speed boundary layer to acoustic disturbances. J. Fluid Mech. 491, 101–129.Google Scholar
Fedorov, A., Shiplyuk, A., Maslov, A., Burov, E. & Malmuth, N. 2003 Stabilization of a hypersonic boundary layer using an ultrasonically absorptive coating. J. Fluid Mech. 479, 99–124.Google Scholar
Fransson, J. H. M., Matsubara, M. & Alfredsson, P. H. 2005 Transition induced by free-stream turbulence. J. Fluid Mech. 527, 1–25.Google Scholar
Goldstein, M. E. 1997 Response of the pre-transitional laminar boundary layer to free-stream turbulence – Otto Laporte Lecture. Bull. Am. Phys. Soc. 42, 2150.Google Scholar
Goldstein, M. E. & Leib, S. J. 1993 Three-dimensional boundary layer instability and separation induced by small-amplitude streamwise vorticity in the upstream flow. J. Fluid Mech. 246, 21–41.CrossRefGoogle Scholar
Goldstein, M. E., Leib, S. J. & Cowley, S. J. 1992 Distortion of a flat plate boundary layer by free stream vorticity normal to the plate. J. Fluid Mech. 237, 231–260.CrossRefGoogle Scholar
Graziosi, P. & Brown, G. L. 2002 Experiments on stability and transition at Mach 3. J. Fluid Mech. 472, 83–124.Google Scholar
Hocking, W. K. 1985 Measurement of turbulent energy dissipation rates in the middle atmosphere by radar techniques: a review. Radio Sci. 20 (6), 1403–1422.Google Scholar
Jacobs, R. G. & Durbin, P. A. 2001 Simulation of bypass transition. J. Fluid Mech. 428, 185–212.Google Scholar
Joo, J. & Durbin, P. 2012 Continuous mode transition in high-speed boundary-layers. Flow Turbul. Combust. 88, 407–430.Google Scholar
Kemp, N.1951 The laminar three-dimensional boundary layer and a study of the flow past a side edge. MSc thesis, Cornell University.Google Scholar
Kendall, J. M.1967 Supersonic boundary layer stability experiments. Tech. Rep. Air Force Report BSD-TR-67-213, vol. II.Google Scholar
Kendall, J. M. 1975 Wind tunnel experiments relating to supersonic and hypersonic boundary-layer transition. AIAA J. 13 (3), 290–299.Google Scholar
Kendall, J. M.1985 Experimental study of disturbances produced in a pre-transitional laminar boundary layer by weak freestream turbulence. AIAA Paper 85-1695.Google Scholar
Kendall, J. M.1990 Boundary layer receptivity to free stream turbulence. AIAA Paper 90-1504.Google Scholar
Kendall, J. M. 1991 Studies on laminar boundary layer receptivity to free-stream turbulence near a leading edge. In Boundary Layer Stability and Transition to Turbulence (ed. Reda, D. C., Reed, H. L. & Kobayashi, R.), vol. 114, pp. 23–30. ASME FED.Google Scholar
Klebanoff, P. S. 1971 Effect of free-stream turbulence on a laminar boundary layer. Bull. Am. Phys. Soc. 16, 1323.Google Scholar
Landahl, M. T. 1989 Unsteady Transonic Flow. Cambridge University Press.Google Scholar
Laufer, J. 1961 Aerodynamic noise in supersonic wind tunnels. J. Aero. Sci. 28 (9), 685–692.Google Scholar
Lees, L.1947 The stability of the laminar boundary layer in a compressible fluid. NACA TN 876.Google Scholar
Leib, S. J., Wundrow, D. W. & Goldstein, M. E. 1999 Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203.CrossRefGoogle Scholar
Li, F. & Malik, M. R. 1996 On the nature of PSE approximation. Theor. Comput. Fluid Dyn. 8 (4), 253–273.Google Scholar
Lighthill, M. J. 1958 On displacement thickness. J. Fluid Mech. 4 (04), 383–392.Google Scholar
Mack, L. M. 1975 Linear stability theory and the problem of supersonic boundary-layer transition. AIAA J. 13 (3), 278–289.Google Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. Special Course on Stability and Transition of Laminar flow, AGARD Report 709, pp. 1–81. Jet Propulsion Laboratory, California Institute of Technology, Pasadena.Google Scholar
Matsubara, M. & Alfredsson, P. H. 2001 Disturbance growth in boundary layers subjected to free-stream turbulence. J. Fluid Mech. 430, 149–168.Google Scholar
Mayer, C. S. J., Von Terzi, D. A. & Fasel, H. F. 2011 Direct numerical simulation of complete transition to turbulence via oblique breakdown at Mach 3. J. Fluid Mech. 674, 5–42.Google Scholar
McKenzie, J. F. & Westphal, K. O. 1968 Interaction of linear waves with oblique shock waves. Phys. Fluids 11 (11), 2350–2362.Google Scholar
Morkovin, M. V. 1984 Bypass transition to turbulence and research desiderata. In NASA CP-2386 Transition in Turbines, pp. 161–204. NASA.Google Scholar
Nagarajan, S., Lele, S. K. & Ferziger, J. H. 2007 Leading-edge effects in bypass transition. J. Fluid Mech. 572, 471–504.CrossRefGoogle Scholar
Ovchinnikov, V., Choudhari, M. M. & Piomelli, U. 2008 Numerical simulations of boundary-layer bypass transition due to high-amplitude free-stream turbulence. J. Fluid Mech. 613, 135–169.Google Scholar
Pate, S. R. & Schueler, C. J. 1969 Radiated aerodynamic noise effects on boundary-layer transition in supersonic and hypersonic wind tunnels. AIAA J. 7 (3), 450–457.Google Scholar
Qin, F. & Wu, X. 2016 Response and receptivity of the hypersonic boundary layer past a wedge to free-stream acoustic, vortical and entropy disturbances. J. Fluid Mech. 797, 874–915.Google Scholar
Ricco, P.2006 Response of a compressible laminar boundary layer to free-stream turbulence. PhD thesis, University of London.Google Scholar
Ricco, P., Luo, J. & Wu, X. 2011 Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances. J. Fluid Mech. 677, 1–38.CrossRefGoogle Scholar
Ricco, P., Shah, D. & Hicks, P. D. 2013 Compressible laminar streaks with wall suction. Phys. Fluids 25, 054110.Google Scholar
Ricco, P., Tran, D.-L. & Ye, G. 2009 Wall heat transfer effects on Klebanoff modes and Tollmien-Schlichting waves in a compressible boundary layer. Phys. Fluids 21, 024106.Google Scholar
Ricco, P. & Wu, X. 2007 Response of a compressible laminar boundary layer to free-stream vortical disturbances. J. Fluid Mech. 587, 97–138.Google Scholar
Riedel, H. & Sitzmann, M. 1998 In-flight investigations of atmospheric turbulence. Aerosp. Sci. Technol. 2 (5), 301–319.Google Scholar
Saad, Y. & Schultz, M. H. 1986 GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 7 (3), 856–869.Google Scholar
Saric, W. S.2008 Flight experiments on local and global effects of surface roughness on 2-d and 3-d boundary-layer stability and transition. Tech. Rep. DTIC Document.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory. Springer.Google Scholar
Schneider, S. P. 1999 Flight data for boundary-layer transition at hypersonic and supersonic speeds. J. Spacecr. Rockets 36 (1), 8–20.Google Scholar
Schneider, S. P. 2001 Effect of high-speed tunnel noise on laminar-turbulent transition. J. Spacecr Rockets 38 (3), 323–333.Google Scholar
Stewartson, K. 1950 On the linearized potential theory of unsteady supersonic motion. Q. J. Mech. Appl. Maths 3 (2), 182–199.Google Scholar
Stewartson, K. 1964 The Theory of Laminar Boundary Layers in Compressible Fluids. Clarendon Press.Google Scholar
Taylor, G. I. 1939 Some recent developments in the study of turbulence. In Proceedings of the Fifth International Congress for Applied Mechanics (ed. Den Hartog, J. P. & Peters, H.), pp. 294–310. Wiley/Chapman and Hall.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scaling in high-Reynolds-number turbulent boundary layers. J. Fluid Mech. 585, 1–40.CrossRefGoogle Scholar
Van Dyke, M. 1975 Perturbation Methods in Fluid Mechanics. Parabolic.Google Scholar
Westin, K. J. A., Bakchinov, A. A., Kozlov, V. V. & Alfredsson, P. H. 1998 Experiments on localized disturbances in a flat plate boundary layer. Part 1. The receptivity and the evolution of a localized free-stream disturbance. Eur. J. Mech. (B/Fluids) 17, 823–846.Google Scholar
Westin, K. J. A., Boiko, A. V., Klingmann, B. G. B., Kozlov, V. V. & Alfredsson, P. H. 1994 Experiments in a boundary layer subjected to free stream turbulence. Part 1. Boundary layer structure and receptivity. J. Fluid Mech. 281, 193–218.Google Scholar
Wilson, R. J., Love, B. J. & Larson, R. R.1971 Evaluation of effects of high-altitude turbulence encounters on the XB-70 airplane. NASA Tech. Rep. NASA/TN D-6457.Google Scholar
Wu, X. & Choudhari, M. 2003 Linear and non-linear instabilities of a Blasius boundary layer perturbed by streamwise vortices. Part 2. Intermittent instability induced by long-wavelength Klebanoff modes. J. Fluid Mech. 483, 249–286.CrossRefGoogle Scholar
Wu, X. & Dong, M. 2016 Entrainment of short-wavelength free-stream vortical disturbances in compressible and incompressible boundary layers. J. Fluid Mech. 797, 683–728.Google Scholar
Wu, X. & Luo, J. 2003 Linear and non-linear instabilities of a Blasius boundary layer perturbed by streamwise vortices. Part 1. Steady streaks. J. Fluid Mech. 483, 225–248.Google Scholar
Wu, X., Zhao, D. & Luo, J. 2011 Excitation of steady and unsteady gortler vortices by free-stream vortical disturbances. J. Fluid Mech. 682, 66–100.Google Scholar
Wundrow, D. W. & Goldstein, M. E. 2001 Effect on a laminar boundary layer of small-amplitude streamwise vorticity in the upstream flow. J. Fluid Mech. 426, 229–262.Google Scholar
Zaki, T. & Durbin, P. A. 2005 Mode interaction and the bypass route to transition. J. Fluid Mech. 531, 85–111.Google Scholar
Zanin, B. Y. 1985 Transition at natural conditions and comparison with the results of wind tunnel studies. In Laminar-Turbulent Transition, pp. 541–546. Springer.Google Scholar
Zhang, Q. & He, L. 2014 Impact of wall temperature on turbine blade tip aerothermal performance. Trans. ASME J. Engng Gas Turbines Power 136 (5), 052602.Google Scholar
Zhang, Y., Zaki, T., Sherwin, S. & Wu, X. 2011 Nonlinear response of a laminar boundary layer to isotropic and spanwise localized free-stream turbulence. In The 6th AIAA Theoretical Fluid Mechanics Conference, p. 3292. American Institute of Aeronautics and Astronautics.Google Scholar
Zhong, X. & Wang, X. 2012 Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 44, 527–561.Google Scholar
Zuccher, S., Bottaro, A. & Luchini, P. 2006 Algebraic growth in a Blasius boundary layer: nonlinear optimal disturbances. Eur. J. Mech. (B/Fluids) 25 (1), 1–17.Google Scholar