Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hewitt, Duncan R.
Neufeld, Jerome A.
and
Lister, John R.
2014.
High Rayleigh number convection in a porous medium containing a thin low-permeability layer.
Journal of Fluid Mechanics,
Vol. 756,
Issue. ,
p.
844.
Nomeli, Mohammad A.
Tilton, Nils
and
Riaz, Amir
2014.
A new model for the density of saturated solutions of CO2–H2O–NaCl in saline aquifers.
International Journal of Greenhouse Gas Control,
Vol. 31,
Issue. ,
p.
192.
Daniel, Don
and
Riaz, Amir
2014.
Effect of viscosity contrast on gravitationally unstable diffusive layers in porous media.
Physics of Fluids,
Vol. 26,
Issue. 11,
Ward, T. J.
Jensen, O. E.
Power, H.
and
Riley, D. S.
2014.
High-Rayleigh-number convection of a reactive solute in a porous medium.
Journal of Fluid Mechanics,
Vol. 760,
Issue. ,
p.
95.
Riaz, Amir
and
Cinar, Yildiray
2014.
Carbon dioxide sequestration in saline formations: Part I—Review of the modeling of solubility trapping.
Journal of Petroleum Science and Engineering,
Vol. 124,
Issue. ,
p.
367.
Daniel, Don
Riaz, Amir
and
Tchelepi, Hamdi A.
2015.
Onset of natural convection in layered aquifers.
Journal of Fluid Mechanics,
Vol. 767,
Issue. ,
p.
763.
Nomeli, Mohammad A.
and
Riaz, Amir
2015.
Handbook of Clean Energy Systems.
p.
1.
Emami-Meybodi, Hamid
Hassanzadeh, Hassan
Green, Christopher P.
and
Ennis-King, Jonathan
2015.
Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments.
International Journal of Greenhouse Gas Control,
Vol. 40,
Issue. ,
p.
238.
Rasmusson, Maria
Fagerlund, Fritjof
Tsang, Yvonne
Rasmusson, Kristina
and
Niemi, Auli
2015.
Prerequisites for density-driven instabilities and convective mixing under broad geological CO2 storage conditions.
Advances in Water Resources,
Vol. 84,
Issue. ,
p.
136.
Vreme, A.
Nadal, F.
Pouligny, B.
Jeandet, P.
Liger-Belair, G.
and
Meunier, P.
2016.
Gravitational instability due to the dissolution of carbon dioxide in a Hele-Shaw cell.
Physical Review Fluids,
Vol. 1,
Issue. 6,
Hitchen, Joseph
and
Wells, Andrew J.
2016.
The impact of imperfect heat transfer on the convective instability of a thermal boundary layer in a porous media.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
p.
154.
Kim, Min Chan
2016.
Effect of swelling on the onset of buoyancy-driven convection during the CO2 dissolution process in a porous medium.
International Journal of Heat and Mass Transfer,
Vol. 100,
Issue. ,
p.
779.
Nomeli, Mohammad A.
and
Riaz, Amir
2017.
Effect of $$\hbox {CO}_2$$ CO 2 solubility on dissolution rate of calcite in saline aquifers for temperature range of 50–100 $$^{\circ } \hbox {C}$$ ∘ C and pressures up to 600 bar: alterations of fractures geometry in carbonate rocks by $$\hbox {CO}_2$$ CO 2 -acidified brines.
Environmental Earth Sciences,
Vol. 76,
Issue. 9,
Rasmusson, M.
Fagerlund, F.
Rasmusson, K.
Tsang, Y.
and
Niemi, A.
2017.
Refractive‐Light‐Transmission Technique Applied to Density‐Driven Convective Mixing in Porous Media With Implications for Geological CO2 Storage.
Water Resources Research,
Vol. 53,
Issue. 11,
p.
8760.
Vo, Liet
and
Hadji, Layachi
2017.
Weakly nonlinear convection induced by the sequestration of CO2 in a perfectly impervious geological formation.
Physics of Fluids,
Vol. 29,
Issue. 12,
Nield, Donald A.
and
Bejan, Adrian
2017.
Convection in Porous Media.
p.
595.
Ghorbani, Zohreh
Riaz, Amir
and
Daniel, Don
2017.
Convective mixing in vertically-layered porous media: The linear regime and the onset of convection.
Physics of Fluids,
Vol. 29,
Issue. 8,
Zhang, Mingkan
Zhang, Ye
and
Lichtner, Peter
2017.
Evaluating model complexity in simulating supercritical CO2 dissolution, leakage, footprint, and reservoir pressure for three-dimensional hierarchical aquifer.
International Journal of Greenhouse Gas Control,
Vol. 64,
Issue. ,
p.
284.
Liang, Yu
Wen, Baole
Hesse, Marc A.
and
DiCarlo, David
2018.
Effect of Dispersion on Solutal Convection in Porous Media.
Geophysical Research Letters,
Vol. 45,
Issue. 18,
p.
9690.
Wen, Baole
and
Chini, Gregory P.
2018.
Reduced modeling of porous media convection in a minimal flow unit at large Rayleigh number.
Journal of Computational Physics,
Vol. 371,
Issue. ,
p.
551.
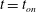 $t=t_{\mathit{on}}$, can be determined from an expansion that is two orders of magnitude faster than a direct numerical simulation. Using the expansion, we explore the sensitivity of
$t=t_{\mathit{on}}$, can be determined from an expansion that is two orders of magnitude faster than a direct numerical simulation. Using the expansion, we explore the sensitivity of 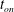 $t_{\mathit{on}}$ to the initial perturbation magnitude and wavelength, as well as the initial time at which a perturbation is initiated. We find that there is an optimal initial time and wavelength that minimize
$t_{\mathit{on}}$ to the initial perturbation magnitude and wavelength, as well as the initial time at which a perturbation is initiated. We find that there is an optimal initial time and wavelength that minimize 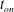 $t_{\mathit{on}}$, and we obtain analytical relationships for these parameters in terms of aquifer properties and initial perturbation magnitude. This importance of the initial perturbation time and magnitude is often overlooked in previous studies. To investigate perturbation evolution at late-times,
$t_{\mathit{on}}$, and we obtain analytical relationships for these parameters in terms of aquifer properties and initial perturbation magnitude. This importance of the initial perturbation time and magnitude is often overlooked in previous studies. To investigate perturbation evolution at late-times, 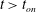 $t>t_{\mathit{on}}$, we perform direct numerical simulations that reveal two unique features of transient diffusive boundary layers. First, when a boundary layer is perturbed with a single horizontal Fourier mode, nonlinear mechanisms generate a zero-wavenumber response whose magnitude eventually surpasses that of the fundamental mode. Second, when a boundary layer is simultaneously perturbed with many Fourier modes, the late-time perturbation magnitude is concentrated in the zero-wavenumber mode, and there is no clearly dominant, non-zero, wavenumber. These unique results are further interpreted by comparison with direct numerical simulations of Rayleigh–Bénard convection.
$t>t_{\mathit{on}}$, we perform direct numerical simulations that reveal two unique features of transient diffusive boundary layers. First, when a boundary layer is perturbed with a single horizontal Fourier mode, nonlinear mechanisms generate a zero-wavenumber response whose magnitude eventually surpasses that of the fundamental mode. Second, when a boundary layer is simultaneously perturbed with many Fourier modes, the late-time perturbation magnitude is concentrated in the zero-wavenumber mode, and there is no clearly dominant, non-zero, wavenumber. These unique results are further interpreted by comparison with direct numerical simulations of Rayleigh–Bénard convection.