Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Qi, Yusheng
Wu, Guangyu
Liu, Yuming
and
Yue, Dick K.P.
2018.
Predictable zone for phase-resolved reconstruction and forecast of irregular waves.
Wave Motion,
Vol. 77,
Issue. ,
p.
195.
Fan, Xiang
Zhang, Jingxin
and
Liu, Hua
2018.
Numerical analysis on the secondary load cycle on a vertical cylinder in steep regular waves.
Ocean Engineering,
Vol. 168,
Issue. ,
p.
133.
Pan, Yulin
Liu, Yuming
and
Yue, Dick K. P.
2018.
On high-order perturbation expansion for the study of long–short wave interactions.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
902.
Liu, Z.
and
Xie, D.
2019.
Finite-amplitude steady-state wave groups with multiple near-resonances in finite water depth.
Journal of Fluid Mechanics,
Vol. 867,
Issue. ,
p.
348.
Stuhlmeier, Raphael
and
Stiassnie, Michael
2019.
Nonlinear dispersion for ocean surface waves.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
49.
Røge Eldrup, Mads
and
Lykke Andersen, Thomas
2019.
Estimation of Incident and Reflected Wave Trains in Highly Nonlinear Two-Dimensional Irregular Waves.
Journal of Waterway, Port, Coastal, and Ocean Engineering,
Vol. 145,
Issue. 1,
Guérin, Charles-Antoine
Desmars, Nicolas
Grilli, Stéphan T.
Ducrozet, Guillaume
Perignon, Yves
and
Ferrant, Pierre
2019.
An improved Lagrangian model for the time evolution of nonlinear surface waves.
Journal of Fluid Mechanics,
Vol. 876,
Issue. ,
p.
527.
Liu, Zeng
Sun, Jianglong
Xie, De
and
Lin, Zhiliang
2019.
On the near resonances of collinear steady-state wave groups in finite water depth.
Ocean Engineering,
Vol. 182,
Issue. ,
p.
584.
Duan, Wenyang
Ma, Xuewen
Huang, Limin
Liu, Yucheng
and
Duan, Shiliang
2020.
Phase-resolved wave prediction model for long-crest waves based on machine learning.
Computer Methods in Applied Mechanics and Engineering,
Vol. 372,
Issue. ,
p.
113350.
Desmars, N.
Bonnefoy, F.
Grilli, S.T.
Ducrozet, G.
Perignon, Y.
Guérin, C.-A.
and
Ferrant, P.
2020.
Experimental and numerical assessment of deterministic nonlinear ocean waves prediction algorithms using non-uniformly sampled wave gauges.
Ocean Engineering,
Vol. 212,
Issue. ,
p.
107659.
Simpson, Alexandra
Haller, Merrick
Walker, David
Lynett, Patrick
and
Honegger, David
2020.
Wave-by-Wave Forecasting via Assimilation of Marine Radar Data.
Journal of Atmospheric and Oceanic Technology,
Vol. 37,
Issue. 7,
p.
1269.
Yan, Zhiyong
Liu, Zeng
and
Li, Ye
2020.
Numerical simulations of collinear finite amplitude steady-state resonant waves in deep water.
Ocean Engineering,
Vol. 212,
Issue. ,
p.
107703.
Korde, Umesh A.
Coe, Ryan G.
and
Bacelli, Giorgio
2020.
Deterministic incident-wave elevation prediction in intermediate water depth.
Journal of Ocean Engineering and Marine Energy,
Vol. 6,
Issue. 4,
p.
359.
Wang, Guangyao
and
Pan, Yulin
2021.
Phase-resolved ocean wave forecast with ensemble-based data assimilation.
Journal of Fluid Mechanics,
Vol. 918,
Issue. ,
Hlophe, Thobani
Wolgamot, Hugh
Kurniawan, Adi
Taylor, Paul H.
Orszaghova, Jana
and
Draper, Scott
2021.
Fast wave-by-wave prediction of weakly nonlinear unidirectional wave fields.
Applied Ocean Research,
Vol. 112,
Issue. ,
p.
102695.
Zinchenko, Victoria
Vasilyev, Leonid
Halstensen, Svein Olav
and
Liu, Yuming
2021.
Short-time deterministic prediction of individual waves based on space-time X-band Marine radar measurements.
Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment,
Vol. 235,
Issue. 2,
p.
356.
Huchet, Marion
Babarit, Aurélien
Ducrozet, Guillaume
Gilloteaux, Jean-Christophe
and
Ferrant, Pierre
2021.
Nonlinear deterministic sea wave prediction using instantaneous velocity profiles.
Ocean Engineering,
Vol. 220,
Issue. ,
p.
108492.
Fu, Ruili
Ma, Yuxiang
Dong, Guohai
and
Perlin, Marc
2021.
A wavelet-based wave group detector and predictor of extreme events over unidirectional sloping bathymetry.
Ocean Engineering,
Vol. 229,
Issue. ,
p.
108936.
Galvagno, M.
Eeltink, D.
and
Stuhlmeier, R.
2021.
Spatial deterministic wave forecasting for nonlinear sea–states.
Physics of Fluids,
Vol. 33,
Issue. 10,
Stuhlmeier, Raphael
and
Stiassnie, Michael
2021.
Deterministic wave forecasting with the Zakharov equation.
Journal of Fluid Mechanics,
Vol. 913,
Issue. ,
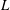 $L$ free wave components of the wave field, accounting for nonlinear wave interactions up to order
$L$ free wave components of the wave field, accounting for nonlinear wave interactions up to order 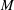 $M$ in the evolution, to obtain a wave field that minimizes the reconstruction error between the reconstructed wave field and the given measurements. For a given reconstruction tolerance,
$M$ in the evolution, to obtain a wave field that minimizes the reconstruction error between the reconstructed wave field and the given measurements. For a given reconstruction tolerance, 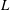 $L$ and
$L$ and  $M$ are provided in the HOR scheme itself. To demonstrate the validity and efficacy of HOR, we perform extensive tests of general two- and three-dimensional wave fields specified by theoretical Stokes waves, nonlinear simulations and physical wave fields in tank experiments which we conduct. The necessary
$M$ are provided in the HOR scheme itself. To demonstrate the validity and efficacy of HOR, we perform extensive tests of general two- and three-dimensional wave fields specified by theoretical Stokes waves, nonlinear simulations and physical wave fields in tank experiments which we conduct. The necessary 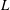 $L$, for general broad-banded wave fields, is shown to be substantially less than the free and locked modes needed for the nonlinear evolution. We find that, even for relatively small wave steepness, the inclusion of high-order effects in HOR is important for prediction of wave kinematics not in the measurements. For all the cases we consider, HOR converges to the underlying wave field within a nonlinear spatial-temporal predictable zone
$L$, for general broad-banded wave fields, is shown to be substantially less than the free and locked modes needed for the nonlinear evolution. We find that, even for relatively small wave steepness, the inclusion of high-order effects in HOR is important for prediction of wave kinematics not in the measurements. For all the cases we consider, HOR converges to the underlying wave field within a nonlinear spatial-temporal predictable zone 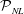 ${\mathcal{P}}_{NL}$ which depends on the measurements and wave nonlinearity. For infinitesimal waves,
${\mathcal{P}}_{NL}$ which depends on the measurements and wave nonlinearity. For infinitesimal waves, 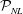 ${\mathcal{P}}_{NL}$ matches the linear predictable zone
${\mathcal{P}}_{NL}$ matches the linear predictable zone 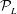 ${\mathcal{P}}_{L}$, verifying the analytic solution presented in Qi et al. (Wave Motion, vol. 77, 2018, pp. 195–213). With increasing wave nonlinearity, we find that
${\mathcal{P}}_{L}$, verifying the analytic solution presented in Qi et al. (Wave Motion, vol. 77, 2018, pp. 195–213). With increasing wave nonlinearity, we find that 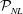 ${\mathcal{P}}_{NL}$ contains and is generally greater than
${\mathcal{P}}_{NL}$ contains and is generally greater than  ${\mathcal{P}}_{L}$. Thus
${\mathcal{P}}_{L}$. Thus 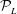 ${\mathcal{P}}_{L}$ provides a (conservative) estimate of
${\mathcal{P}}_{L}$ provides a (conservative) estimate of 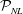 ${\mathcal{P}}_{NL}$ when the underlying wave field is not known.
${\mathcal{P}}_{NL}$ when the underlying wave field is not known.


