Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-18T00:15:10.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear instability and convection in a vertically vibrated granular bed

Published online by Cambridge University Press:  17 November 2014

Priyanka Shukla ,
Istafaul H. Ansari ,
Devaraj van der Meer ,
Detlef Lohse  and
Meheboob Alam
Priyanka Shukla
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Istafaul H. Ansari
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Devaraj van der Meer
Affiliation:
Physics of Fluids Group, Department of Science and Technology and JM Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Detlef Lohse
Affiliation:
Physics of Fluids Group, Department of Science and Technology and JM Burgers Center for Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands
Meheboob Alam*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The nonlinear instability of the density-inverted granular Leidenfrost state and the resulting convective motion in strongly shaken granular matter are analysed via a weakly nonlinear analysis of the hydrodynamic equations. The base state is assumed to be quasi-steady and the effect of harmonic shaking is incorporated by specifying a constant granular temperature at the vibrating plate. Under these mean-field assumptions, the base-state temperature decreases with increasing height away from the vibrating plate, but the density profile consists of three distinct regions: (i) a collisional dilute layer at the bottom, (ii) a levitated dense layer at some intermediate height and (iii) a ballistic dilute layer at the top of the granular bed. For the nonlinear stability analysis (Shukla & Alam, J. Fluid Mech., vol. 672, 2011b, pp. 147–195), the nonlinearities up to cubic order in the perturbation amplitude are retained, leading to the Landau equation, and the related adjoint stability problem is formulated taking into account appropriate boundary conditions. The first Landau coefficient and the related modal eigenfunctions (the fundamental mode and its adjoint, the second harmonic and the base-flow distortion, and the third harmonic and the cubic-order distortion to the fundamental mode) are calculated using a spectral-based numerical method. The genesis of granular convection is shown to be tied to a supercritical pitchfork bifurcation from the density-inverted Leidenfrost state. Near the bifurcation point the equilibrium amplitude (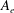$A_{e}$) is found to follow a square-root scaling law, 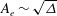$A_{e}\sim \sqrt{{\it\Delta}}$, with the distance 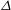${\it\Delta}$ from the bifurcation point. We show that the strength of convection (measured in terms of velocity circulation) is maximal at some intermediate value of the shaking strength, with weaker convection at both weaker and stronger shaking. Our theory predicts that at very strong shaking the convective motion remains concentrated only near the top surface, with the bulk of the expanded granular bed resembling the conduction state of a granular gas, dubbed as a floating-convection state. The linear and nonlinear patterns of the density and velocity fields are analysed and compared with experiments qualitatively. Evidence of 2:1 resonance is shown for certain parameter combinations. The influences of bulk viscosity, effective Prandtl number, shear work and free-surface boundary conditions on nonlinear equilibrium states are critically assessed.

JFM classification

Complex Fluids: Complex Fluids Convection: Convection Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 123 - 167
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Nonlinear Physical Chemistry Unit, Faculté des Sciences, Université libre de Bruxelles, 1050 Brussels, Belgium.

References

Alam, M., Arakeri, V. H., Nott, P. R., Goddard, J. D. & Herrmann, H. J. 2005 Instability-induced ordering, universal unfolding and the role of gravity in granular Couette flow. J. Fluid Mech. 523, 277–306.CrossRefGoogle Scholar
Alam, M., Chikkadi, V. & Gupta, V. K. 2009 Density waves and the effect of wall roughness in granular Poiseuille flow: simulation and linear stability. Eur. Phys. J. 179, 69–90 (Special Topics).Google Scholar
Alam, M. & Nott, P. R. 1998 Stability of plane Couette flow of a granular material. J. Fluid Mech. 377, 99–136.Google Scholar
Alam, M. & Shukla, P. 2012 Origin of subcritical shearbanding instability in a dense two-dimensional sheared granular fluid. Granul. Matt. 14, 221–227.CrossRefGoogle Scholar
Alam, M. & Shukla, P. 2013 Nonlinear stability, bifurcation and vortical patterns in three-dimensional granular plane Couette flow. J. Fluid Mech. 716, 349–413.Google Scholar
Alam, M., Shukla, P. & Luding, S. 2008 Universality of shear-banding instability and crystallization in sheared granular fluid. J. Fluid Mech. 615, 293–321.Google Scholar
Alam, M., Trujillo, L. & Herrmann, H. J. 2006 Hydrodynamic theory for reverse Brazil nut segregation and the non-monotonic ascension dynamics. J. Stat. Phys. 124, 587–623.Google Scholar
Almazan, L., Carrillo, J. A., Saluena, C., Garzo, V. & Pöschel, P. 2013 A numerical study of the Navier–Stokes transport coefficients for two-dimensional granular hydrodynamics. New J. Phys. 15, 043044.Google Scholar
Ansari, I. & Alam, M. 2013 Patterns and velocity field in vertically vibrated granular materials. In AIP Conference Proceedings (ed. Yu, A., Dong, K., Yang, R. & Luding, S.), vol. 1542, pp. 775–778.Google Scholar
Ansari, I. & Alam, M. 2014 Dynamics of density-inverted/Leidenfrost state in a vibrofluidized bed. Bull. Am. Phys. Soc. (67th Annual Meeting of the APS Division of Fluid Dynamics) 59 (20), (Abstract Number: G.24.00008).Google Scholar
Aoki, K. M., Akiyoma, T., Maki, Y. & Watanabe, T. 1996 Convective roll patterns in vertically vibrated beds of granules. Phys. Rev. E 54, 874–882.Google Scholar
Bizon, C., Shattuck, M. D., Swift, J. B., McCormick, W. D. & Swinney, H. L. 1998 Patterns in 3D vertically oscillated granular layers: simulation and experiment. Phys. Rev. Lett. 80, 57–60.Google Scholar
Bourzutschky, M. & Miller, J. 1995 Granular convection in a vibrated fluid. Phys. Rev. Lett. 74, 2216–2219.Google Scholar
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Carrillo, J. A., Pöschel, T. & Saluena, C. 2007 Granular hydrodynamics and pattern formation in vertically oscillated granular disk layers. J. Fluid Mech. 597, 119–144.Google Scholar
Chandrashekar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Dover.Google Scholar
Chladni, E. F. F. 1787 Entdeckungen über die Theorie des Klanges. Kessinger.Google Scholar
Clément, E., Duran, J. & Rajchenbach, J. 1992 Experimental study of heaping in a two-dimensional sand pile. Phys. Rev. Lett. 69, 1189–1192.Google Scholar
Douady, S., Fauve, S. & Laroche, C. 1992 Subharmonic instabilities and defects in a granular layer under vertical vibrations. Europhys. Lett. 8, 621–626.Google Scholar
Eshuis, P., van der Meer, D., Alam, M., van Gerner, H. J., van der Weele, K. & Lohse, D. 2010 Onset convection in strongly shaken granular matter. Phys. Rev. Lett. 104, 038001.Google Scholar
Eshuis, P., van der Weele, K., Alam, M., van Gerner, H. J., van der Höf, M., Kuipers, H., Luding, S., van der Meer, D. & Lohse, D. 2013 Buoyancy driven convection in vertically shaken granular matter: experiment, numerics, and theory. Granul. Matt. 15, 893–911.Google Scholar
Eshuis, P., van der Weele, K., van der Meer, D., Bos, R. & Lohse, D. 2007 Phase diagram of vertically shaken granular matter. Phys. Fluids 19, 123301.Google Scholar
Eshuis, P., van der Weele, K., van der Meer, D. & Lohse, D. 2005 Granular Leidenfrost effect: experiment and theory of floating particle clusters. Phys. Rev. Lett. 95, 258001.Google Scholar
Faraday, M. 1831 On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Phil. Trans. R. Soc. Lond. 52, 299–318.Google Scholar
Forterre, Y. & Pouliquen, O. 2002 Stability analysis of rapid granular chute flows: formation of longitudinal vortices. J. Fluid Mech. 467, 361–387.Google Scholar
Gallas, J. A. C., Herrmann, H. J. & Sokolowski, S. 1992 Convection cells in vibrating granular media. Phys. Rev. Lett. 69, 1371–1374.Google Scholar
Garzo, V., Santos, A. & Montanero, J. M. 2007 Modified Sonine approximation for the Navier–Stokes transport coefficients of a granular gas. Physica A 376, 94–107.Google Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195–233.Google Scholar
Gebhart, B., Jaluria, Y., Mahajan, R. L. & Sammakia, B. 1988 Buoyancy-Induced Flows and Transport. Springer.Google Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.Google Scholar
Golub, G. H. & van Loan, C. F. 1989 Matrix Computations, 2nd edn. The Johns Hopkins University Press.Google Scholar
Grossman, E. L., Zhou, T. & Ben-Naim, E. 1997 Towards granular hydrodynamics in two dimensions. Phys. Rev. Lett. 55, 4200–4206.Google Scholar
Haff, P. K. 1983 Grain flow as a fluid mechanical phenomenon. J. Fluid Mech. 134, 401–430.Google Scholar
Hayakawa, H., Yue, S. & Hong, D. C. 1995 Hydrodynamic description of granular convection. Phys. Rev. Lett. 75, 2328–2331.Google Scholar
Hui, K., Haff, P. K., Ungar, J. E. & Jackson, R. 1984 Boundary conditions for high-shear grain flows. J. Fluid Mech. 145, 223–233.Google Scholar
Jackson, R. 2000 Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985a Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985b Kinetic theory of plane flows of a dense gas of identical, rough, inelastic, circular disks. Phys. Fluids 28, 3485–3494.Google Scholar
Jenkins, J. T. & Richman, M. W. 1986 Boundary conditions for plane flows of smooth, nearly elastic, circular disks. J. Fluid Mech. 171, 53–69.Google Scholar
Khain, E. & Meerson, B. 2003 Onset of thermal convection in a horizontal layer of granular gas. Phys. Rev. E 67, 021306.Google Scholar
Knight, J. B., Ehrichs, E. E., Kuperman, V. Y., Flint, J. K., Jaeger, H. M. & Nagel, S. R. 1996 Experimental study of granular convection. Phys. Rev. E 54, 5726–5738.CrossRefGoogle ScholarPubMed
Lakkaraju, R. & Alam, M. 2007 Effects of Prandtl number and a new instability mode in a plane thermal plume. J. Fluid Mech. 592, 221–231.Google Scholar
Lan, Y. & Rosato, A. D. 1997 Convection related phenomena in granular dynamics simulations of vibrated beds. Phys. Fluids 9, 3615–3627.Google Scholar
Luding, S., Clement, E., Blumen, A., Rajchenbach, J. & Duran, J. 1994 The onset of convection in molecular dynamics simulations of grains. Phys. Rev. E 50, R1762–1765.Google Scholar
Meerson, B., Pöschel, T. & Bromberg, Y. 2003 Close-packed floating clusters: granular hydrodynamics beyond a freezing point? Phys. Rev. Lett. 91, 024301.Google Scholar
Ohtsuki, T. & Ohsawa, T. 2003 Hydrodynamics for convection in vibrating beds of cohesionless granular materials. J. Phys. Soc. Japan 72, 1963–1967.Google Scholar
Olafsen, J. S. & Urbach, J. S. 1998 Clustering, order, and collapse in a driven granular monolayer. Phys. Rev. Lett. 81, 4369–4372.Google Scholar
Paolotti, D., Barrat, A., Marconi, U. M. B. & Puglisi, A. 2004 Thermal convection in monodisperse and bidisperse granular gases: a simulation study. Phys. Rev. E 69, 061304.Google Scholar
Park, H. K. & Behringer, R. P. 1992 Surface waves in vertically vibrated granular materials. Phys. Rev. Lett. 71, 1832–1835.Google Scholar
Pöschel, T. & Herrmann, H. J. 1995 Size segregation and convection. Europhys. Lett. 29, 124–128.Google Scholar
Ramirez, R., Risso, D. & Cordero, P. 2000 Thermal convection in fluidized granular systems. Phys. Rev. Lett. 85, 1230–1233.Google Scholar
Rao, K. K. R. & Nott, P. R. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Reynolds, W. C. & Potter, M. C. 1967 Finite amplitude instability of parallel shear flows. J. Fluid Mech. 27, 465–492.Google Scholar
Saha, S. & Alam, M. 2014 Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method. J. Fluid Mech. 757, 251–296.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres. J. Fluid Mech. 361, 41–74.Google Scholar
Shinbrot, T. & Muzzio, F. J. 1998 Reverse buoyancy in shaken granular beds. Phys. Rev. Lett. 81, 4365–4368.Google Scholar
Shukla, P. & Alam, M. 2009 Order parameter description of shear-banding in granular Couette flow via Landau equation. Phys. Rev. Lett. 103, 068001.Google Scholar
Shukla, P. & Alam, M. 2011a Weakly nonlinear theory of shear-banding instability in granular plane Couette flow: analytical solution, comparison with numerics and bifurcation. J. Fluid Mech. 666, 204–253.CrossRefGoogle Scholar
Shukla, P. & Alam, M. 2011b Nonlinear stability and patterns in granular plane Couette flow: Hopf and pitchfork bifurcations, and evidence for resonance. J. Fluid Mech. 672, 147–195.Google Scholar
Shukla, P. & Alam, M. 2013 Nonlinear vorticity banding instability in granular plane Couette flow: higher order Landau coefficient, bistability and the bifurcation scenario. J. Fluid Mech. 718, 131–180.Google Scholar
Stuart, J. T. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 353–370.Google Scholar
Sunthar, P. & Kumaran, V. 2001 Characterization of the stationary states of a dilute vibrofluidized granular bed. Phys. Rev. E 64, 041303.Google Scholar
Umbanhower, P. B., Melo, F. & Swinney, H. L. 1996 Localized excitations in a vertically vibrated granular layer. Nature 382, 793–796.Google Scholar
Viswanathan, H., Sheikh, N. A., Wildman, R. D. & Huntley, J. M. 2011 Convection in three-dimensional vibrofluidized granular beds. J. Fluid Mech. 682, 185–212.Google Scholar
Watson, J. 1960 On the nonlinear mechanics of wave disturbances in stable and unstable parallel flows. J. Fluid Mech. 9, 371–389.Google Scholar
Wildman, R. D., Huntley, J. M. & Parker, D. J. 2001 Convection in highly fluidized three-dimensional granular beds. Phys. Rev. Lett. 86, 3304–3307.Google Scholar
Woodhouse, M. J. & Hogg, A. J. 2010 Rapid granular flows down inclined planar chutes. Part 2. Linear stability analysis of steady flow solutions. J. Fluid Mech. 652, 461–488.Google Scholar