Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T00:43:52.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear exact coherent structures in pipe flow and their instabilities

Published online by Cambridge University Press:  15 April 2019

Ozge Ozcakir Open the ORCID record for Ozge Ozcakir [Opens in a new window] ,
Philip Hall  and
Saleh Tanveer
Ozge Ozcakir*
Affiliation:
School of Mathematical Sciences, Monash University, Clayton, VIC 3800, Australia
Philip Hall
Affiliation:
School of Mathematical Sciences, Monash University, Clayton, VIC 3800, Australia
Saleh Tanveer
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we present computational results of some two-fold azimuthally symmetric travelling waves and their stability. Calculations over a range of Reynolds numbers (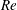$Re$) reveal connections between a class of solutions computed by Wedin & Kerswell (J. Fluid Mech., vol. 508, 2004, pp. 333–371) (henceforth called the WK solution) and the 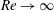$Re\rightarrow \infty$ vortex–wave interaction theory of Hall & Smith (J. Fluid Mech., vol. 227, 1991, pp. 641–666) and Hall & Sherwin (J. Fluid Mech., vol. 661, 2010, pp. 178–205). In particular, the continuation of the WK solutions to larger values of 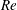$Re$ shows that the WK solution bifurcates from a shift-and-rotate symmetric solution, which we call the WK2 state. The WK2 solution computed for 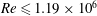$Re\leqslant 1.19\times 10^{6}$ shows excellent agreement with the theoretical $Re^{-5/6}$, 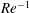$Re^{-1}$ and 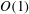$O(1)$ scalings of the waves, rolls and streaks respectively. Furthermore, these states are found to have only two unstable modes in the large 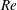$Re$ regime, with growth rates estimated to be 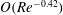$O(Re^{-0.42})$ and $O(Re^{-0.92})$, close to the theoretical 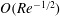$O(Re^{-1/2})$ and 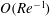$O(Re^{-1})$ asymptotic results for edge and sinuous instability modes of vortex–wave interaction states (Deguchi & Hall, J. Fluid Mech., vol. 802, 2016, pp. 634–666) in plane Couette flow. For the nonlinear viscous core states (Ozcakir et al., J. Fluid Mech., vol. 791, 2016, pp. 284–328), characterized by spatial a shrinking of the wave and roll structure towards the pipe centre with increasing $Re$, we continued the solution to 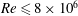$Re\leqslant 8\times 10^{6}$ and we find only one unstable mode in the large Reynolds number regime, with growth rate scaling as 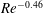$Re^{-0.46}$ within the class of symmetry-preserving disturbances.

JFM classification

Instability: Transition to turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 341 - 368
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackburn, H. M., Hall, P. & Sherwin, S. J. 2013 Lower branch equilibria in Couette flow: the emergence of canonical states for arbitrary shear flows. J. Fluid Mech. 726, R2.Google Scholar
Budanur, N. B. & Hof, B. 2018 Complexity of the laminar-turbulent boundary in pipe flow. Phys. Fluids 3, 054401.Google Scholar
Budanur, N. B., Short, K. Y., Farazmand, M., Willis, A. P. & Cvitanovic, P. 2017 Relative periodic orbits form the backbone of turbulent pipe flow. J. Fluid Mech. 833, 274–301.Google Scholar
Chantry, M., Willis, A. P. & Kerswell, R. R. 2014 Genesis of streamwise-localized solutions from globally periodic traveling waves in pipe flow. Phys. Rev. Lett. 112, 164501.Google Scholar
Deguchi, K. & Hall, P. 2014a The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow. J. Fluid Mech. 750, 99–112.Google Scholar
Deguchi, K. & Hall, P. 2014b Free-stream coherent structures in parallel boundary-layer flows. J. Fluid Mech. 752, 602–625.Google Scholar
Deguchi, K. & Hall, P. 2016 On the instabilities of vortex–wave interaction states. J. Fluid Mech. 802, 634–666.Google Scholar
Duguet, Y., Pringle, C. C. T. & Kerswell, R. R. 2008a Relative periodic orbits in transitional pipe flow. Phys. Fluids 20, 1141102.Google Scholar
Duguet, Y., Willis, A. P. & Kerswell, R. R. 2008b Transition in pipe flow: the saddle structure on the boundary of turbulence. J. Fluid Mech. 613, 255–274.Google Scholar
Faisst, H. & Eckhardt, B. 2003 Traveling waves in pipe flow. Phys. Rev. Lett. 91, 224502.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2009 Equilibrium and travelling-wave solutions of plane Couette flow. J. Fluid Mech. 638, 243–266.Google Scholar
Hall, P. & Sherwin, S. 2010 Streamwise vortices in shear flows: harbingers of transition and the skeleton of coherent structures. J. Fluid Mech. 661, 178–205.Google Scholar
Hall, P. & Smith, F. 1991 On strongly nonlinear vortex/wave interactions in boundary layer transition. J. Fluid Mech. 227, 641–666.Google Scholar
Hof, B., van Doorne, C., Westerweel, J., Nieuwstadt, F., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in the turbulent pipe flow. Science 305 (5690), 1594–1598.Google Scholar
Kerswell, R. & Tutty, O. 2007 Recurrence of traveling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Nagata, M. 1990 Three dimensional finite-amplitude solutions in plane Coutte flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Ozcakir, O., Tanveer, S., Hall, P. & Overman, E. A. 2016 Travelling waves in pipe flow. J. Fluid Mech. 791, 284–328.Google Scholar
Pringle, C. C. T., Duguet, Y. & Kerswell, R. R. 2009 Highly symmetric travelling waves in pipe flow. Phil. Trans. R. Soc. Lond. A 367 (1888), 457–472.Google Scholar
Pringle, C. C. T & Kerswell, R. R. 2007 Asymmetric, helical and mirror-symmetric travelling waves in pipe flow. Phys. Rev. Lett. 99, 074502.Google Scholar
Soibelman, I. & Meiron, D. 1991 Finite-amplitude bifurcations in plane Poiseuille flow: two-dimensional Hopf bifurcation. J. Fluid Mech. 229, 389–416.Google Scholar
Toh, S. & Itano, T. 2003 A periodic-like solution in channel flow. J. Fluid Mech. 481, 67–76.Google Scholar
Viswanath, D. 2007 Recurrent motions within plane Couette turbulence. J. Fluid Mech. 580, 339–358.Google Scholar
Viswanath, D. 2009 Critical layer in pipe flow at high Reynolds number. Phil. Trans. R. Soc. Lond. A 580, 561–576.Google Scholar
Viswanath, D. & Cvitanovic, P. 2009 Stable manifolds and the transition to turbulence in pipe flow. J. Fluid Mech. 627, 215–233.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95 (3), 319–343.Google Scholar
Waleffe, F. 2001 Exact coherent structures in channel flow. J. Fluid Mech. 435, 93–102.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15 (6), 1517–1534.Google Scholar
Wang, J., Gibson, J. & Waleffe, F. 2007 Lower branch coherent states in shear flows: transition and control. Phys. Rev. Lett. 98 (20), 204501.Google Scholar
Wedin, H. & Kerswell, R. 2004 Exact coherent structures in pipe flow: travelling wave solutions. J. Fluid Mech. 508, 333–371.Google Scholar
Willis, A. P., Duguet, Y., Omel’chenko, O. & Wolfrum, M. 2017 Surfing the edge: using feedback control to find nonlinear solutions. J. Fluid Mech. 831, 579–591.Google Scholar