Published online by Cambridge University Press: 06 March 2008
We present high-resolution direct numerical simulations of the nonlinear evolution of a pair of counter-rotating vertical vortices in a stratified fluid for various high Reynolds numbers Re and low Froude numbers Fh. The vortices are bent by the zigzag instability producing high vertical shear. There is no nonlinear saturation so that the exponential growth is stopped only when the viscous dissipation by vertical shear is of the same order as the horizontal transport, i.e. when 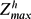 /Re=O(1) where
/Re=O(1) where 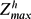 is the maximum horizontal enstrophy non-dimensionalized by the vortex turnover frequency. The zigzag instability therefore directly transfers the energy from large scales to the small dissipative vertical scales. However, for high Reynolds number, the vertical shear created by the zigzag instability is so intense that the minimum local Richardson number Ri decreases below a threshold of around 1/4 and small-scale Kelvin–Helmholtz instabilities develop. We show that this can only occur when
is the maximum horizontal enstrophy non-dimensionalized by the vortex turnover frequency. The zigzag instability therefore directly transfers the energy from large scales to the small dissipative vertical scales. However, for high Reynolds number, the vertical shear created by the zigzag instability is so intense that the minimum local Richardson number Ri decreases below a threshold of around 1/4 and small-scale Kelvin–Helmholtz instabilities develop. We show that this can only occur when 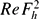 is above a threshold estimated as 340. Movies are available with the online version of the paper.
is above a threshold estimated as 340. Movies are available with the online version of the paper.
Movie 1. Pseudo-spectral numerical simulation of the nonlinear evolution of a pair of counter-rotating vertical vortices in a stratified fluid for a Froude number F_h = 0.66 and a Reynolds number Re = 1060 (run labelled F0.6R1 in the paper). The vortices, initially straight along the vertical, are bent as a whole by the zigzag instability producing high vertical shear. Vertical vorticity isosurfaces are plotted: red and deep blue contours represent respectively plus and minus 60% of the vertical average of the maximum vertical vorticity in each horizontal plane. Transparent yellowish and bluish isosurfaces are the same, but for a 10% level.