Published online by Cambridge University Press: 28 March 2018
We investigate electrophoresis of a tightly fitting sphere of radius 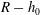 $R-h_{0}$ on the axis of a circular tube of radius
$R-h_{0}$ on the axis of a circular tube of radius 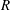 $R$, using lubrication theory and ideas due to Schnitzer & Yariv (Phys. Fluids, vol. 26, 2014, 122002). The electrical charge clouds on both the cylindrical wall and the surface of the sphere are assumed thin compared to the gap between the sphere and cylinder, so that charge clouds do not overlap and ion exclusion effects are minimal. Nevertheless, non-uniform pumping of counter-ions within the charge clouds leads to a change in the ionic concentration outside the charge clouds in the narrow gap between sphere and cylinder. The electro-osmotic slip velocities at the two surfaces are modified, leading to a decrease in the electrophoretic velocity of the sphere at low Péclet numbers and an increase in the velocity at high Péclet numbers. When the field strength
$R$, using lubrication theory and ideas due to Schnitzer & Yariv (Phys. Fluids, vol. 26, 2014, 122002). The electrical charge clouds on both the cylindrical wall and the surface of the sphere are assumed thin compared to the gap between the sphere and cylinder, so that charge clouds do not overlap and ion exclusion effects are minimal. Nevertheless, non-uniform pumping of counter-ions within the charge clouds leads to a change in the ionic concentration outside the charge clouds in the narrow gap between sphere and cylinder. The electro-osmotic slip velocities at the two surfaces are modified, leading to a decrease in the electrophoretic velocity of the sphere at low Péclet numbers and an increase in the velocity at high Péclet numbers. When the field strength 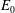 $E_{0}$ is low, it is known that the electrophoretic velocity
$E_{0}$ is low, it is known that the electrophoretic velocity 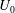 $U_{0}$ is proportional to
$U_{0}$ is proportional to  $E_{0}(\unicode[STIX]{x1D701}_{s}-\unicode[STIX]{x1D701}_{c})$ which is zero when the zeta potential
$E_{0}(\unicode[STIX]{x1D701}_{s}-\unicode[STIX]{x1D701}_{c})$ which is zero when the zeta potential 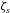 $\unicode[STIX]{x1D701}_{s}$ on the sphere surface is equal to the zeta potential
$\unicode[STIX]{x1D701}_{s}$ on the sphere surface is equal to the zeta potential 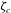 $\unicode[STIX]{x1D701}_{c}$ on the cylinder. The perturbation to the above low field strength electrophoretic velocity (at high Péclet number) is predicted to be proportional to
$\unicode[STIX]{x1D701}_{c}$ on the cylinder. The perturbation to the above low field strength electrophoretic velocity (at high Péclet number) is predicted to be proportional to 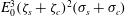 $E_{0}^{3}(\unicode[STIX]{x1D701}_{s}+\unicode[STIX]{x1D701}_{c})^{2}(\unicode[STIX]{x1D70E}_{s}+\unicode[STIX]{x1D70E}_{c})$, where
$E_{0}^{3}(\unicode[STIX]{x1D701}_{s}+\unicode[STIX]{x1D701}_{c})^{2}(\unicode[STIX]{x1D70E}_{s}+\unicode[STIX]{x1D70E}_{c})$, where 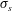 $\unicode[STIX]{x1D70E}_{s}$ and
$\unicode[STIX]{x1D70E}_{s}$ and 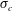 $\unicode[STIX]{x1D70E}_{c}$ are the surface charge densities on the sphere and cylinder. The choice of materials with similar or identical zeta potentials (and surface charge densities) for the cylinder and sphere should therefore facilitate the observation of velocities nonlinear in the field strength
$\unicode[STIX]{x1D70E}_{c}$ are the surface charge densities on the sphere and cylinder. The choice of materials with similar or identical zeta potentials (and surface charge densities) for the cylinder and sphere should therefore facilitate the observation of velocities nonlinear in the field strength 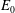 $E_{0}$, since the reference linear electrophoretic velocity will be small.
$E_{0}$, since the reference linear electrophoretic velocity will be small.