Published online by Cambridge University Press: 25 November 2016
We consider the time dependence of a hierarchy of scaled 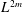 $L^{2m}$-norms
$L^{2m}$-norms  $D_{m,\unicode[STIX]{x1D714}}$ and
$D_{m,\unicode[STIX]{x1D714}}$ and 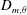 $D_{m,\unicode[STIX]{x1D703}}$ of the vorticity
$D_{m,\unicode[STIX]{x1D703}}$ of the vorticity 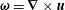 $\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$ and the density gradient
$\unicode[STIX]{x1D74E}=\unicode[STIX]{x1D735}\times \boldsymbol{u}$ and the density gradient 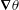 $\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$, where
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$, where 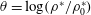 $\unicode[STIX]{x1D703}=\log (\unicode[STIX]{x1D70C}^{\ast }/\unicode[STIX]{x1D70C}_{0}^{\ast })$, in a buoyancy-driven turbulent flow as simulated by Livescu & Ristorcelli (J. Fluid Mech., vol. 591, 2007, pp. 43–71). Here,
$\unicode[STIX]{x1D703}=\log (\unicode[STIX]{x1D70C}^{\ast }/\unicode[STIX]{x1D70C}_{0}^{\ast })$, in a buoyancy-driven turbulent flow as simulated by Livescu & Ristorcelli (J. Fluid Mech., vol. 591, 2007, pp. 43–71). Here, 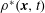 $\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},t)$ is the composition density of a mixture of two incompressible miscible fluids with fluid densities
$\unicode[STIX]{x1D70C}^{\ast }(\boldsymbol{x},t)$ is the composition density of a mixture of two incompressible miscible fluids with fluid densities  $\unicode[STIX]{x1D70C}_{2}^{\ast }>\unicode[STIX]{x1D70C}_{1}^{\ast }$, and
$\unicode[STIX]{x1D70C}_{2}^{\ast }>\unicode[STIX]{x1D70C}_{1}^{\ast }$, and 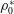 $\unicode[STIX]{x1D70C}_{0}^{\ast }$ is a reference normalization density. Using data from the publicly available Johns Hopkins turbulence database, we present evidence that the
$\unicode[STIX]{x1D70C}_{0}^{\ast }$ is a reference normalization density. Using data from the publicly available Johns Hopkins turbulence database, we present evidence that the 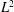 $L^{2}$-spatial average of the density gradient
$L^{2}$-spatial average of the density gradient 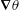 $\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ can reach extremely large values at intermediate times, even in flows with low Atwood number
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ can reach extremely large values at intermediate times, even in flows with low Atwood number 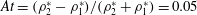 $At=(\unicode[STIX]{x1D70C}_{2}^{\ast }-\unicode[STIX]{x1D70C}_{1}^{\ast })/(\unicode[STIX]{x1D70C}_{2}^{\ast }+\unicode[STIX]{x1D70C}_{1}^{\ast })=0.05$, implying that very strong mixing of the density field at small scales can arise in buoyancy-driven turbulence. This large growth raises the possibility that the density gradient
$At=(\unicode[STIX]{x1D70C}_{2}^{\ast }-\unicode[STIX]{x1D70C}_{1}^{\ast })/(\unicode[STIX]{x1D70C}_{2}^{\ast }+\unicode[STIX]{x1D70C}_{1}^{\ast })=0.05$, implying that very strong mixing of the density field at small scales can arise in buoyancy-driven turbulence. This large growth raises the possibility that the density gradient 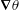 $\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ might blow up in a finite time.
$\unicode[STIX]{x1D735}\unicode[STIX]{x1D703}$ might blow up in a finite time.