Published online by Cambridge University Press: 06 March 2017
Using simple kinematics, we propose a general theory of linear wave interactions between the interfacial waves of a two-dimensional (2D), inviscid, multilayered fluid system. The strength of our formalism is that one does not have to specify the physics of the waves in advance. Wave interactions may lead to instabilities, which may or may not be of the familiar ‘normal-mode’ type. Contrary to intuition, the underlying dynamical system describing linear wave interactions is found to be nonlinear. Specifically, a saw-tooth jet profile with three interfaces possessing kinematic and geometric symmetry is explored. Fixed points of the system for different ranges of a Froude number like control parameter 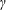 $\unicode[STIX]{x1D6FE}$ are derived, and their stability evaluated. Depending upon the initial condition and
$\unicode[STIX]{x1D6FE}$ are derived, and their stability evaluated. Depending upon the initial condition and 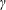 $\unicode[STIX]{x1D6FE}$, the dynamical system may reveal transient growth, weakly positive Lyapunov exponents, as well as different nonlinear phenomena such as the formation of periodic and pseudo-periodic orbits. All these occur for those ranges of
$\unicode[STIX]{x1D6FE}$, the dynamical system may reveal transient growth, weakly positive Lyapunov exponents, as well as different nonlinear phenomena such as the formation of periodic and pseudo-periodic orbits. All these occur for those ranges of 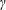 $\unicode[STIX]{x1D6FE}$ where normal-mode theory predicts neutral stability. Such rich nonlinear phenomena are not observed in a 2D dynamical system resulting from the two-wave problem, which reveals only stable and unstable nodes.
$\unicode[STIX]{x1D6FE}$ where normal-mode theory predicts neutral stability. Such rich nonlinear phenomena are not observed in a 2D dynamical system resulting from the two-wave problem, which reveals only stable and unstable nodes.