Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T21:48:34.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-isothermal droplet spreading/dewetting and its reversal

Published online by Cambridge University Press:  03 July 2015

Yi Sui  and
Peter D. M. Spelt
Yi Sui
Affiliation:
School of Engineering and Materials Science, Queen Mary University of London, Mile End Road, London E1 4NS, UK
Peter D. M. Spelt*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique (LMFA), CNRS, Ecole Centrale Lyon, 36 avenue Guy de Collongue, 69134 Ecully, France Département Mécanique, Université Claude Bernard Lyon 1, 43 Boulevard du 11 novembre 1918, 69622 Villeurbanne, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Axisymmetric non-isothermal spreading/dewetting of droplets on a substrate is studied, wherein the surface tension is a function of temperature, resulting in Marangoni stresses. A lubrication theory is first extended to determine the drop shape for spreading/dewetting limited by slip. It is demonstrated that an apparent angle inferred from a fitted spherical cap shape does not relate to the contact-line speed as it would under isothermal conditions. Also, a power law for the thermocapillary spreading rate versus time is derived. Results obtained with direct numerical simulations (DNS), using a slip length down to 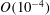$O(10^{-4})$ times the drop diameter, confirm predictions from lubrication theory. The DNS results further show that the behaviour predicted by the lubrication theory – that a cold wall promotes spreading, and a hot wall promotes dewetting – is reversed at sufficiently large contact angles and/or viscosity of the surrounding fluid. This behaviour is summarized in a phase diagram, and a simple model that supports this finding is presented. Although the key results are found to be robust when accounting for heat conduction in the substrate, a critical thickness of the substrate is identified above which wall conduction significantly modifies wetting behaviour.

JFM classification

Interfacial Flows (free surface): Contact lines Drops and Bubbles: Thermocapillarity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 74 - 95
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.CrossRefGoogle Scholar
Bostwick, J. B. 2013 Spreading and bistability of droplets on differentially heated substrates. J. Fluid Mech. 725, 566–587.CrossRefGoogle Scholar
Brackbill, J. U., Kothe, D. B. & Zemach, C. 1992 A continuum method for modeling surface tension. J. Comput. Phys. 100, 335–354.CrossRefGoogle Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Craster, R. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.CrossRefGoogle Scholar
Davis, S. H. 2000 Interfacial fluid dynamics. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G.), Cambridge University Press.Google Scholar
Dunn, G. J., Wilson, S. K., Duffy, B. R., David, S. & Sefiane, K. 2009 The strong influence of substrate conductivity on droplet evaporation. J. Fluid Mech. 623, 329–351.Google Scholar
Ehrhard, P. 1993 Experiments on isothermal and nonisothermal spreading. J. Fluid Mech. 257, 463–483.Google Scholar
Ehrhard, P. & Davis, S. H. 1991 Non-isothermal spreading of liquid drops on horizontal plates. J. Fluid Mech. 229, 365–388.Google Scholar
Greenspan, H. P. 1977 On the motion of a small viscous droplet that wets a surface. J. Fluid Mech. 84, 125–143.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Herrmann, M., Lopez, J. M., Brady, P. & Raessi, M. 2008 Thermocapillary motion of deformable drops and bubbles. In Proceedings of the Summer Program 2008, pp. 155–170. Center for Turbulence Research.Google Scholar
Hocking, L. M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Maths 36, 55–69.Google Scholar
Hocking, L. M. 1992 Rival contact-angle models and the spreading of drops. J. Fluid Mech. 239, 671–681.Google Scholar
Hocking, L. M. & Rivers, A. D. 1982 The spreading of a drop by capillary action. J. Fluid Mech. 121, 425–442.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.CrossRefGoogle Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.Google Scholar
Ren, W. & E, W. 2007 Boundary conditions for the moving contact line problem. Phys. Fluids 68, 016306.Google Scholar
Ristenpart, W. D., Kim, P. G., Domingues, C., Wan, J. & Stone, H. A. 2007 Influence of substrate conductivity on circulation reversal in evaporating drops. Phys. Rev. Lett. 99, 234502.CrossRefGoogle ScholarPubMed
Sibley, D. N., Nold, A. & Kalliadasis, S. 2015a The asymptotics of the moving contact line: cracking an old nut. J. Fluid Mech. 764, 445–462.CrossRefGoogle Scholar
Sibley, D. N., Nold, A., Savva, N. & Kalliadasis, S. 2015b A comparison of slip, disjoining pressure, and interface formation models for contact line motion through asymptotic analysis of thin two-dimensional droplet spreading. J. Engng Maths (in press), doi:10.1007/s10665-014-9702-9.Google Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales regimes, and dynamical transitions. Annu. Rev. Fluid Mech. 45, 269–292.Google Scholar
Sui, Y. 2014 Moving towards the cold region or the hot region? Thermocapillary migration of a droplet attached on a horizontal substrate. Phys. Fluids 26, 092102.Google Scholar
Sui, Y., Ding, H. & Spelt, P. D. M. 2014 Numerical simulation of moving contact-line flows. Annu. Rev. Fluid Mech. 46, 97–119.Google Scholar
Sui, Y. & Spelt, P. D. M. 2013a Validation and modification of asymptotic analysis of slow and rapid droplet spreading by numerical simulation. J. Fluid Mech. 715, 283–313.Google Scholar
Sui, Y. & Spelt, P. D. M. 2013b An efficient computational model for macroscale simulations of moving contact lines. J. Comput. Phys. 242, 37–52.Google Scholar
Sussman, M., Almgren, G. S., Bell, G. B., Colella, P., Howell, L. H. & Welcome, M. L. 1999 An adaptive level set approach for incompressible two-phase flows. J. Comput. Phys. 148, 81–124.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D 12, 1473–1483.Google Scholar
Young, N. O., Goldstein, J. S. & Block, M. J. 1959 The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 6, 350–356.Google Scholar