Published online by Cambridge University Press: 18 July 2019
The non-dimensional dissipation rate 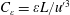 $C_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D700}L/u^{\prime 3}$, where
$C_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D700}L/u^{\prime 3}$, where  $\unicode[STIX]{x1D700}$,
$\unicode[STIX]{x1D700}$, 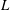 $L$ and
$L$ and 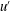 $u^{\prime }$ are the viscous energy dissipation rate, integral length scale of turbulence and root-mean-square of the velocity fluctuations, respectively, is computed and analysed within the turbulent/non-turbulent interfacial (TNTI) layer using direct numerical simulations of a planar jet, mixing layer and shear free turbulence. The TNTI layer that separates the turbulent and non-turbulent regions exists at the edge of free shear turbulent flows and turbulent boundary layers, and comprises both the viscous superlayer and turbulent sublayer regions. The computation of
$u^{\prime }$ are the viscous energy dissipation rate, integral length scale of turbulence and root-mean-square of the velocity fluctuations, respectively, is computed and analysed within the turbulent/non-turbulent interfacial (TNTI) layer using direct numerical simulations of a planar jet, mixing layer and shear free turbulence. The TNTI layer that separates the turbulent and non-turbulent regions exists at the edge of free shear turbulent flows and turbulent boundary layers, and comprises both the viscous superlayer and turbulent sublayer regions. The computation of 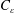 $C_{\unicode[STIX]{x1D700}}$ is made possible by the introduction of an original procedure, based on local volume averages within spheres of radius
$C_{\unicode[STIX]{x1D700}}$ is made possible by the introduction of an original procedure, based on local volume averages within spheres of radius  $r$, combined with conditional sampling as a function of the location with respect to the TNTI layer. The new procedure allows for a detailed investigation of the scale dependence of several turbulent quantities near the TNTI layer. An important achievement of this procedure consists in permitting the computation of the turbulent integral scale within the TNTI layer, which is shown to be approximately constant. Both the non-dimensional dissipation rate and turbulent Reynolds number
$r$, combined with conditional sampling as a function of the location with respect to the TNTI layer. The new procedure allows for a detailed investigation of the scale dependence of several turbulent quantities near the TNTI layer. An important achievement of this procedure consists in permitting the computation of the turbulent integral scale within the TNTI layer, which is shown to be approximately constant. Both the non-dimensional dissipation rate and turbulent Reynolds number 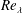 $Re_{\unicode[STIX]{x1D706}}$ vary in space within the TNTI layer, where two relations are observed:
$Re_{\unicode[STIX]{x1D706}}$ vary in space within the TNTI layer, where two relations are observed: 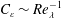 $C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-1}$ and
$C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-1}$ and 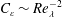 $C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-2}$. Specifically, whereas the viscous superlayer and part of the turbulent sublayer display
$C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-2}$. Specifically, whereas the viscous superlayer and part of the turbulent sublayer display 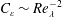 $C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-2}$, the remaining of the turbulent sublayer exhibits
$C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-2}$, the remaining of the turbulent sublayer exhibits 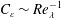 $C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-1}$, which is consistent with non-equilibrium turbulence (Vassilicos, Annu. Rev. Fluid Mech. vol. 47, 2015, pp. 95–114).
$C_{\unicode[STIX]{x1D700}}\sim Re_{\unicode[STIX]{x1D706}}^{-1}$, which is consistent with non-equilibrium turbulence (Vassilicos, Annu. Rev. Fluid Mech. vol. 47, 2015, pp. 95–114).