1. Introduction
The statistical understanding of water waves is a topic of significant interest to oceanographers, physicists and engineers. Knowledge regarding the probability of encountering extreme surface elevations and wave heights is especially important e.g. in the design of marine structures, the analysis of wave loads on offshore wind turbines or oil platforms, as well as in ensuring safe maritime operations.
Methods for studying the statistical properties of irregular wave fields include analysis of e.g. second-order irregular waves (e.g. Forristall Reference Forristall2000), laboratory experiments (e.g. Onorato et al. Reference Onorato2009; Toffoli et al. Reference Toffoli, Gramstad, Trulsen, Monbaliu, Bitner-Gregersen and Onorato2010; Lawrence, Trulsen & Gramstad Reference Lawrence, Trulsen and Gramstad2022), field measurements (e.g. Karmpadakis, Swan & Christou Reference Karmpadakis, Swan and Christou2020) or numerical models (e.g. Socquet-Juglard et al. Reference Socquet-Juglard, Dysthe, Trulsen, Krogstad and Liu2005; Toffoli et al. Reference Toffoli, Benoit, Onorato and Bitner-Gregersen2009; Xiao et al. Reference Xiao, Liu, Wu and Yue2013; Klahn, Madsen & Fuhrman Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb; Tang & Adcock Reference Tang and Adcock2021; Zhang & Benoit Reference Zhang and Benoit2021; Liu et al. Reference Liu, Zhang, Yang and Yao2022; Tang et al. Reference Tang, Barratt, Bingham, van den Bremer and Adcock2022). These are, of course, in addition to theoretical means (e.g. Longuet-Higgins Reference Longuet-Higgins1963; Song & Wu Reference Song and Wu2000), which have often been developed under simplifying narrow-band approximations and/or unidirectional assumptions (e.g. Longuet-Higgins Reference Longuet-Higgins1952; Tayfun Reference Tayfun1980; Tayfun & Alkhalidi Reference Tayfun and Alkhalidi2020).
Among the most fundamentally important statistical descriptions of an irregular sea is the probability density function (p.d.f.) of the free surface elevation itself. Presently, the predominant means for theoretically computing this p.d.f. for a nonlinear, irregular gravity water wave field, free of assumptions involving narrow-bandedness and small directionality, remains the classical solution of Longuet-Higgins (Reference Longuet-Higgins1963), hereafter referred to as Reference Longuet-HigginsLH63. Utilizing the inverse Fourier transform of the cumulant generating function, Reference Longuet-HigginsLH63 derived an approximation of the resulting p.d.f. in the form of a Gram–Charlier series. To leading order his result is Gaussian, whereas his approximate distribution accounts for the leading-order effects of both skewness (beginning at second order) and kurtosis (beginning at third order).
In the present paper, we shall re-visit the classical derivation of the probability density of the surface elevation in irregular seas, to second order in the wave steepness. To the order retained, p.d.f.s will be derived from both moment and cumulant generating functions. It will be shown that, although his derivation was based on the cumulant generating function, the approximation arrived at by Reference Longuet-HigginsLH63, in fact, corresponds to that from the moment generating function. By invoking a change in variables, coupled with complex analysis, it will be newly shown that the p.d.f. stemming from the cumulant generating function can, in fact, be formulated exactly, rather than approximately, in terms of the Airy Ai function. It will be shown that this new p.d.f. exhibits a heavier positive tail than those of Reference Longuet-HigginsLH63 i.e. increased probability density of large surface elevations. A practical means for remedying spurious non-physical oscillations which arise in the probability density of negative surface elevations will likewise be devised, valid for irregular wave fields having skewness less than or equal to approximately 0.2. The resulting p.d.f.s will be compared with those based on results generated from both second-order irregular wave theory (Madsen & Fuhrman Reference Madsen and Fuhrman2012) as well as from fully nonlinear, spectrally accurate numerical simulations, utilizing the model of Klahn, Madsen & Fuhrman (Reference Klahn, Madsen and Fuhrman2021c).
The remainder of this paper is organized as follows: p.d.f.s to second order in the wave steepness are first derived in § 2, utilizing both moment and cumulant generating functions. The relationship to the p.d.f. of Reference Longuet-HigginsLH63 is discussed in § 3. Asymptotic limits of the p.d.f.s for large surface elevations are provided and compared in § 4. Practical considerations regarding implementation of the new p.d.f. are discussed in § 5, including a semi-theoretical means of remedying spurious oscillations in the negative tail. The accuracy of the new p.d.f.s is tested in § 6, with a practical example application based on sample data provided in § 7. Conclusions are finally drawn in § 8.
2. Probability density functions derived from moment and cumulant generating functions
Let ![]() $\eta$ denote the free surface elevation and
$\eta$ denote the free surface elevation and ![]() $\sigma$ its standard deviation, with
$\sigma$ its standard deviation, with ![]() $\zeta \equiv \eta / \sigma$. In the form of a Stokes-type perturbation series
$\zeta \equiv \eta / \sigma$. In the form of a Stokes-type perturbation series ![]() $\zeta$ can be represented as
$\zeta$ can be represented as
in which the first-order wave field, ![]() $\zeta _1$, is
$\zeta _1$, is ![]() $O(1)$, the second-order correction,
$O(1)$, the second-order correction, ![]() $\zeta _2$, is
$\zeta _2$, is ![]() $O(\varepsilon )$, and so forth, where
$O(\varepsilon )$, and so forth, where ![]() $\varepsilon$ is a a characteristic wave steepness. In the following sections, we derive the p.d.f. of
$\varepsilon$ is a a characteristic wave steepness. In the following sections, we derive the p.d.f. of ![]() $\zeta$ using both its moment and cumulant generating functions to second order in the wave steepness, by which we mean that we retain all terms that are
$\zeta$ using both its moment and cumulant generating functions to second order in the wave steepness, by which we mean that we retain all terms that are ![]() $O(1)$ and
$O(1)$ and ![]() $O(\varepsilon )$, but neglect all terms proportional to
$O(\varepsilon )$, but neglect all terms proportional to ![]() $\varepsilon ^n$ with
$\varepsilon ^n$ with ![]() $n \geqslant 2$. We assume that the coordinate system is chosen such that
$n \geqslant 2$. We assume that the coordinate system is chosen such that ![]() $\zeta$ has zero mean.
$\zeta$ has zero mean.
2.1. The second-order p.d.f. of  $\zeta$ derived from the moment generating function
$\zeta$ derived from the moment generating function
The moment generating function of ![]() $\zeta$,
$\zeta$, ![]() $M_\zeta (s)$, is defined as
$M_\zeta (s)$, is defined as
where ![]() $s$ is a dimensionless (possibly complex) variable and
$s$ is a dimensionless (possibly complex) variable and ![]() $\langle {\cdot } \rangle$ denotes the expectation operator. Letting
$\langle {\cdot } \rangle$ denotes the expectation operator. Letting ![]() $p(\zeta )$ denote the p.d.f. of
$p(\zeta )$ denote the p.d.f. of ![]() $\zeta$ and substituting
$\zeta$ and substituting ![]() $i s$ for
$i s$ for ![]() $s$ gives the integral equation
$s$ gives the integral equation
which is readily inverted for ![]() $p(\zeta )$ by means of the inverse Fourier transform
$p(\zeta )$ by means of the inverse Fourier transform
Thus, it is seen that one way to obtain the p.d.f. of a random variable is through the inverse Fourier transform of its moment generating function. Now, to compute the moment generating function of ![]() $\zeta$, we make use of its power series form
$\zeta$, we make use of its power series form
 \begin{equation} M_\zeta(s) = \sum_{q = 0}^{\infty} \frac{s^q}{q!} \langle \zeta^q \rangle, \end{equation}
\begin{equation} M_\zeta(s) = \sum_{q = 0}^{\infty} \frac{s^q}{q!} \langle \zeta^q \rangle, \end{equation}
which can be derived by Taylor expanding the exponential function in (2.2) and exploiting the linearity of the expectation operator. To compute the moments we will consider the cases where ![]() $q$ is even and odd separately.
$q$ is even and odd separately.
When ![]() $q$ is even we may write
$q$ is even we may write ![]() $q = 2m$, where
$q = 2m$, where ![]() $m$ is a non-negative integer, and hence
$m$ is a non-negative integer, and hence
upon using (2.1). The binomial theorem then gives that
 \begin{equation} \langle \zeta^{q} \rangle = \sum_{n = 0}^{2m} {2m \choose n} \langle \zeta_1^{2m-n} \zeta_2^{n} \rangle, \end{equation}
\begin{equation} \langle \zeta^{q} \rangle = \sum_{n = 0}^{2m} {2m \choose n} \langle \zeta_1^{2m-n} \zeta_2^{n} \rangle, \end{equation}
where ![]() $(\begin{smallmatrix}{2m}\\ {n}\end{smallmatrix})$ is the
$(\begin{smallmatrix}{2m}\\ {n}\end{smallmatrix})$ is the ![]() $2m$ choose
$2m$ choose ![]() $n$ binomial coefficient. Assuming
$n$ binomial coefficient. Assuming ![]() $\zeta _1$ to be a linear combination of sine waves with random, independent phases implies that any term containing an odd power of
$\zeta _1$ to be a linear combination of sine waves with random, independent phases implies that any term containing an odd power of ![]() $\zeta _1$ vanishes. By additionally assuming their frequencies to be densely distributed, to second order in the wave steepness, we have
$\zeta _1$ vanishes. By additionally assuming their frequencies to be densely distributed, to second order in the wave steepness, we have
where the second equality above may be shown to hold using arguments identical to those used by e.g. Reference Longuet-HigginsLH63 (see e.g. his p. 462) in addition to Song & Wu (Reference Song and Wu2000) or Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a) (their § 4.1.1). The last equality follows from the fact that ![]() $\zeta$, by definition, has unit variance i.e. to second order
$\zeta$, by definition, has unit variance i.e. to second order ![]() $\langle \zeta ^2\rangle =\langle \zeta _1^2\rangle =1$. We note that the even moments are
$\langle \zeta ^2\rangle =\langle \zeta _1^2\rangle =1$. We note that the even moments are ![]() $O(1)$.
$O(1)$.
When ![]() $q$ is odd we may instead write
$q$ is odd we may instead write ![]() $q = 2m+1$, and using the same arguments as above, we find that
$q = 2m+1$, and using the same arguments as above, we find that
when keeping the terms consistent with the second-order approximation. Again using a calculation analogous to that of Song & Wu (Reference Song and Wu2000) (see their Appendix), this result may further be shown to be
where it has been used that, to second order, the skewness is ![]() $\mathcal {S} \equiv \langle \zeta ^3\rangle =3\langle \zeta _1^2\zeta _2\rangle$, which we note is
$\mathcal {S} \equiv \langle \zeta ^3\rangle =3\langle \zeta _1^2\zeta _2\rangle$, which we note is ![]() $O(\varepsilon )$. Combining the even and odd moments with the power series form of the moment generating function (2.5), and shifting indices in the odd terms, then gives
$O(\varepsilon )$. Combining the even and odd moments with the power series form of the moment generating function (2.5), and shifting indices in the odd terms, then gives
 \begin{equation} M_\zeta(s) = \sum_{q = 0}^{\infty} \frac{1}{q!} \left( \frac{s^2}{2} \right)^q \left( 1 + \frac{1}{6} \mathcal{S} s^3 \right) = \exp\left( \frac{s^2}{2} \right) \left( 1 + \frac{1}{6} \mathcal{S} s^3 \right). \end{equation}
\begin{equation} M_\zeta(s) = \sum_{q = 0}^{\infty} \frac{1}{q!} \left( \frac{s^2}{2} \right)^q \left( 1 + \frac{1}{6} \mathcal{S} s^3 \right) = \exp\left( \frac{s^2}{2} \right) \left( 1 + \frac{1}{6} \mathcal{S} s^3 \right). \end{equation}It now follows from (2.4) that, to second order in the wave steepness, the moment generating function predicts the p.d.f. of the surface elevation to be
Upon integrating, the result is
This concludes our derivation of the p.d.f. of the surface elevation based on the moment generating function.
Interestingly, the resulting expression for ![]() $p(\zeta )$ above was also found to second order by Reference Longuet-HigginsLH63, who based his derivation on the cumulant generating function, rather than the moment generating function utilized above. His derivation will be briefly reviewed and discussed further in § 3.
$p(\zeta )$ above was also found to second order by Reference Longuet-HigginsLH63, who based his derivation on the cumulant generating function, rather than the moment generating function utilized above. His derivation will be briefly reviewed and discussed further in § 3.
2.2. The second-order p.d.f. of  $\zeta$ derived from the cumulant generating function
$\zeta$ derived from the cumulant generating function
From the above it is seen that obtaining the p.d.f. of ![]() $\zeta$ from its moment generating function requires the calculation of an infinite number of moments. This is due to the fact that each moment, in general, consists of a first-order contribution, a second-order contribution and so on. In that regard utilizing the cumulant generating function of
$\zeta$ from its moment generating function requires the calculation of an infinite number of moments. This is due to the fact that each moment, in general, consists of a first-order contribution, a second-order contribution and so on. In that regard utilizing the cumulant generating function of ![]() $\zeta$,
$\zeta$, ![]() $C_\zeta (s)$ is much simpler, as its terms are ordered in powers of
$C_\zeta (s)$ is much simpler, as its terms are ordered in powers of ![]() $\varepsilon$. It is defined as
$\varepsilon$. It is defined as
Moreover, the cumulants of ![]() $\zeta$ correspond directly to the coefficients
$\zeta$ correspond directly to the coefficients ![]() $C_q$ in the Taylor expansion
$C_q$ in the Taylor expansion
 \begin{equation} C_\zeta(s) = \sum_{q = 1}^{\infty} \frac{C_q}{q!} s^q. \end{equation}
\begin{equation} C_\zeta(s) = \sum_{q = 1}^{\infty} \frac{C_q}{q!} s^q. \end{equation}Upon insertion of the power series form of the moment generating function (2.5) into (2.14), and then Taylor expanding the logarithm, one finds that the first three cumulants are
and that all other cumulants are ![]() $O(\varepsilon ^2)$ or smaller. To second order in the wave steepness the cumulant generating function thus reads
$O(\varepsilon ^2)$ or smaller. To second order in the wave steepness the cumulant generating function thus reads
Combining this result with (2.14) and (2.4) then implies that
where it has been utilized that the sign of imaginary terms within the exponential may be freely reversed without modifying the integral. To work out the integral, we start by making a change of variables. Setting
 \begin{equation} s = \left( \frac{2}{\mathcal{S}}\right)^{1/3} \tau - \frac{{\rm i}}{\mathcal{S}} \end{equation}
\begin{equation} s = \left( \frac{2}{\mathcal{S}}\right)^{1/3} \tau - \frac{{\rm i}}{\mathcal{S}} \end{equation}transforms the integral to
 \begin{equation} p(\zeta) = \frac{1}{2{\rm \pi}} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{-\infty + {\rm i}\gamma}^{\infty + {\rm i}\gamma} \exp \left( {\rm i} \left( \frac{\tau^3}{3} + \chi \tau \right) \right) \mathrm{d}\tau, \end{equation}
\begin{equation} p(\zeta) = \frac{1}{2{\rm \pi}} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{-\infty + {\rm i}\gamma}^{\infty + {\rm i}\gamma} \exp \left( {\rm i} \left( \frac{\tau^3}{3} + \chi \tau \right) \right) \mathrm{d}\tau, \end{equation}in which
and
 \begin{equation} \chi = \left(\frac{2}{\mathcal{S}} \right)^{1/3} \left( \frac{1}{2 \mathcal{S}} + \zeta \right)\end{equation}
\begin{equation} \chi = \left(\frac{2}{\mathcal{S}} \right)^{1/3} \left( \frac{1}{2 \mathcal{S}} + \zeta \right)\end{equation} are introduced for notational convenience. Now, (2.20) is a contour integral in the complex plane with the contour being a straight line lying a distance ![]() $\gamma$ above the real line. However, as we will now show, the contour can be pushed down to the real line. To demonstrate this, consider the contour integral
$\gamma$ above the real line. However, as we will now show, the contour can be pushed down to the real line. To demonstrate this, consider the contour integral
 \begin{equation} \int_{\varGamma} \exp \left( {\rm i} \left( \frac{z^3}{3} + \chi z \right) \right) \mathrm{d} z = \sum_{n=1}^4 \underbrace{\int_{\varGamma_n} \exp \left( {\rm i} \left( \frac{z^3}{3} + \chi z \right) \right) \mathrm{d} z}_{I_n} \equiv \sum_{n=1}^4 I_n, \end{equation}
\begin{equation} \int_{\varGamma} \exp \left( {\rm i} \left( \frac{z^3}{3} + \chi z \right) \right) \mathrm{d} z = \sum_{n=1}^4 \underbrace{\int_{\varGamma_n} \exp \left( {\rm i} \left( \frac{z^3}{3} + \chi z \right) \right) \mathrm{d} z}_{I_n} \equiv \sum_{n=1}^4 I_n, \end{equation}
where the contour ![]() $\varGamma$, and its sub-contours, are defined in figure 1 and should be considered in the limit
$\varGamma$, and its sub-contours, are defined in figure 1 and should be considered in the limit ![]() $R \rightarrow \infty$. Since the integrand is analytic, the residue theorem implies that the integral along
$R \rightarrow \infty$. Since the integrand is analytic, the residue theorem implies that the integral along ![]() $\varGamma$ is exactly zero (see e.g. Berg Reference Berg2013) for any value of
$\varGamma$ is exactly zero (see e.g. Berg Reference Berg2013) for any value of ![]() $R$. Hence, if it can be proved that
$R$. Hence, if it can be proved that ![]() $I_2$ and
$I_2$ and ![]() $I_4$ vanish when
$I_4$ vanish when ![]() $R$ becomes large, we will have shown that (2.20) may, in fact, be evaluated by integrating along the real line. Considering
$R$ becomes large, we will have shown that (2.20) may, in fact, be evaluated by integrating along the real line. Considering ![]() $I_2$ first, it is clear that
$I_2$ first, it is clear that
If we parameterize ![]() $\varGamma _2$ letting
$\varGamma _2$ letting ![]() $z(\delta ) = R + i\gamma (1-\delta )$ with
$z(\delta ) = R + i\gamma (1-\delta )$ with ![]() $0 \leqslant \delta \leqslant 1$, and utilize the fact that
$0 \leqslant \delta \leqslant 1$, and utilize the fact that ![]() $\gamma$ is positive, this leads directly to
$\gamma$ is positive, this leads directly to
Now, since ![]() $(1-\delta )^3\leqslant (1-\delta )$ over the range of
$(1-\delta )^3\leqslant (1-\delta )$ over the range of ![]() $\delta$ considered, we may replace the former with the latter in the final (positive) term within the exponential. This then yields that
$\delta$ considered, we may replace the former with the latter in the final (positive) term within the exponential. This then yields that
and working out the integral then gives that
and hence
whose limit is zero as ![]() $R\to \infty$. We have thus shown that
$R\to \infty$. We have thus shown that ![]() $I_2$ vanishes in this limit. As an identical argument can be used to show that
$I_2$ vanishes in this limit. As an identical argument can be used to show that ![]() $I_4$ also becomes negligible when
$I_4$ also becomes negligible when ![]() $R$ becomes large, we do not present it here, but conclude that the contour in (2.23) can indeed be pushed down to the real line. Doing so yields
$R$ becomes large, we do not present it here, but conclude that the contour in (2.23) can indeed be pushed down to the real line. Doing so yields
 \begin{equation} p(\zeta) = \frac{1}{2{\rm \pi}} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{-\infty}^{\infty } \exp \left( {\rm i} \left( \frac{\tau^3}{3} + \chi \tau \right) \right) \mathrm{d}\tau. \end{equation}
\begin{equation} p(\zeta) = \frac{1}{2{\rm \pi}} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{-\infty}^{\infty } \exp \left( {\rm i} \left( \frac{\tau^3}{3} + \chi \tau \right) \right) \mathrm{d}\tau. \end{equation}
Since the argument of the exponential function in the integrand is an odd function of ![]() $\tau$, using the polar form of the integrand gives
$\tau$, using the polar form of the integrand gives
 \begin{equation} p(\zeta) = \frac{1}{\rm \pi} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{0}^{\infty } \cos \left( \frac{\tau^3}{3} + \chi \tau \right) \mathrm{d}\tau. \end{equation}
\begin{equation} p(\zeta) = \frac{1}{\rm \pi} \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \int_{0}^{\infty } \cos \left( \frac{\tau^3}{3} + \chi \tau \right) \mathrm{d}\tau. \end{equation}This may be equivalently written as
 \begin{equation} p(\zeta) = \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \text{Ai} (\chi), \end{equation}
\begin{equation} p(\zeta) = \left( \frac{2}{\mathcal{S}}\right)^{1/3} \exp \left( \frac{1}{3 \mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right) \text{Ai} (\chi), \end{equation}where
defines the integral representation of the Airy function of the first kind, which is explicitly available in most any mathematical software or programming language.

Figure 1. The contour ![]() $\varGamma = \cup _{n = 1}^4 \varGamma _n$, which should be considered in the limit where
$\varGamma = \cup _{n = 1}^4 \varGamma _n$, which should be considered in the limit where ![]() $R$ tends to
$R$ tends to ![]() $\infty$. The arrows indicate the direction of integration along the segments.
$\infty$. The arrows indicate the direction of integration along the segments.
The result found in (2.31) is new, and seemingly corresponds to the first time the second-order p.d.f. has been derived from the cumulant generating function, without resorting to any further approximation.
2.3. Asymptotic equivalence of the two approaches for small steepness
At first glance, the p.d.f.s derived from the moment (2.13) and cumulant generating functions (2.31) appear quite different. However, they are both second-order approximations of the exact p.d.f., and it is therefore natural to expect that they become equivalent in the limit of small wave steepness. In this section we demonstrate that this is indeed the case by showing that (2.31) reduces to (2.13) when ![]() $\varepsilon$ is small.
$\varepsilon$ is small.
To do so, we start by noting that, when ![]() $\varepsilon$ is small,
$\varepsilon$ is small, ![]() $\mathcal {S}$ becomes small, and hence
$\mathcal {S}$ becomes small, and hence ![]() $\chi$ becomes large. For large, positive and real arguments (see e.g. Abramowitz & Stegun Reference Abramowitz and Stegun1964) the asymptotic form of the Airy function is
$\chi$ becomes large. For large, positive and real arguments (see e.g. Abramowitz & Stegun Reference Abramowitz and Stegun1964) the asymptotic form of the Airy function is
 \begin{equation} \text{Ai}(\chi) \sim \frac{1}{2 {\rm \pi}^{1/2} \chi^{1/4}} \exp\left( - \frac{2}{3} \chi^{3/2} \right) \sum_{n = 0}^{\infty} \frac{ \left( -\frac{3}{4} \right)^n \, \varGamma \left(n + \frac{5}{6} \right) \varGamma \left(n + \frac{1}{6} \right)}{2{\rm \pi} n! \chi^{3n/2}}. \end{equation}
\begin{equation} \text{Ai}(\chi) \sim \frac{1}{2 {\rm \pi}^{1/2} \chi^{1/4}} \exp\left( - \frac{2}{3} \chi^{3/2} \right) \sum_{n = 0}^{\infty} \frac{ \left( -\frac{3}{4} \right)^n \, \varGamma \left(n + \frac{5}{6} \right) \varGamma \left(n + \frac{1}{6} \right)}{2{\rm \pi} n! \chi^{3n/2}}. \end{equation}
Since ![]() $\chi \sim \varepsilon ^{-4/3}$ in the limit
$\chi \sim \varepsilon ^{-4/3}$ in the limit ![]() $\varepsilon \rightarrow 0$, the
$\varepsilon \rightarrow 0$, the ![]() $n$th term in the series is asymptotically of order
$n$th term in the series is asymptotically of order ![]() $\varepsilon ^{2n}$. For consistency with the assumption made in the previous section, we only retain terms up to
$\varepsilon ^{2n}$. For consistency with the assumption made in the previous section, we only retain terms up to ![]() $O(\varepsilon )$, and by using that
$O(\varepsilon )$, and by using that ![]() $\varGamma (5/6) \varGamma (1/6) = 2{\rm \pi}$, we obtain
$\varGamma (5/6) \varGamma (1/6) = 2{\rm \pi}$, we obtain
Now, a first-order Taylor series expansion in ![]() $\mathcal {S}$ of
$\mathcal {S}$ of ![]() $(1 + 2 \mathcal {S} \zeta )^{-1/4}$ yields
$(1 + 2 \mathcal {S} \zeta )^{-1/4}$ yields
 \begin{equation} \frac{1}{2 {\rm \pi}^{1/2} \chi^{1/4}} = \frac{1}{\sqrt{2{\rm \pi}}} \left(\frac{2}{\mathcal{S}} \right)^{-1/3} \left( 1 - \frac{1}{2} \mathcal{S} \zeta + O ( \varepsilon^2 ) \right). \end{equation}
\begin{equation} \frac{1}{2 {\rm \pi}^{1/2} \chi^{1/4}} = \frac{1}{\sqrt{2{\rm \pi}}} \left(\frac{2}{\mathcal{S}} \right)^{-1/3} \left( 1 - \frac{1}{2} \mathcal{S} \zeta + O ( \varepsilon^2 ) \right). \end{equation}
Moreover, from a third-order Taylor series expansion of ![]() $(1 + 2 \mathcal {S} \zeta )^{3/2}$ it follows that
$(1 + 2 \mathcal {S} \zeta )^{3/2}$ it follows that
 \begin{align} \exp \left( -\frac{2}{3} \chi^{3/2} \right) & = \exp \left( - \frac{1}{3 \mathcal{S}^2} \left( 1 + 3 \mathcal{S} \zeta + \frac{3}{2} \mathcal{S}^2 \zeta^2 - \frac{1}{2} \mathcal{S}^3 \zeta^3 + O (\varepsilon^4) \right)\right) \nonumber\\ & = \exp \left( - \frac{1}{3 \mathcal{S}^2} - \frac{\zeta}{\mathcal{S}} - \frac{\zeta^2}{2} \right) \left( 1 + \frac{\mathcal{S}}{6} \zeta^3 + O (\varepsilon^2) \right). \end{align}
\begin{align} \exp \left( -\frac{2}{3} \chi^{3/2} \right) & = \exp \left( - \frac{1}{3 \mathcal{S}^2} \left( 1 + 3 \mathcal{S} \zeta + \frac{3}{2} \mathcal{S}^2 \zeta^2 - \frac{1}{2} \mathcal{S}^3 \zeta^3 + O (\varepsilon^4) \right)\right) \nonumber\\ & = \exp \left( - \frac{1}{3 \mathcal{S}^2} - \frac{\zeta}{\mathcal{S}} - \frac{\zeta^2}{2} \right) \left( 1 + \frac{\mathcal{S}}{6} \zeta^3 + O (\varepsilon^2) \right). \end{align}Hence, we may rewrite the asymptotic approximation of the Airy function as
 \begin{equation} \text{Ai}(\chi) = \frac{1}{\sqrt{2{\rm \pi}}} \left(\frac{2}{\mathcal{S}} \right)^{-1/3} \exp \left( - \frac{1}{3 \mathcal{S}^2} - \frac{\zeta}{\mathcal{S}} - \frac{\zeta^2}{2} \right) \left( 1 + \frac{\mathcal{S}}{6} (\zeta^3 - 3\zeta ) + O ( \varepsilon^2 ) \right). \end{equation}
\begin{equation} \text{Ai}(\chi) = \frac{1}{\sqrt{2{\rm \pi}}} \left(\frac{2}{\mathcal{S}} \right)^{-1/3} \exp \left( - \frac{1}{3 \mathcal{S}^2} - \frac{\zeta}{\mathcal{S}} - \frac{\zeta^2}{2} \right) \left( 1 + \frac{\mathcal{S}}{6} (\zeta^3 - 3\zeta ) + O ( \varepsilon^2 ) \right). \end{equation}Inserting this into (2.31), we then find that
which matches the result seen in (2.13). Thus, we have shown that the second-order results implied by the moment and cumulant generating functions are asymptotically equivalent in the limit of small wave steepness. Obviously, both reduce to the Gaussian (normal) distribution
in the linear limit.
3. Discussion of Longuet-Higgins (Reference Longuet-Higgins1963)
Reference Longuet-HigginsLH63 based the derivation of his p.d.f. on the cumulant generating function, carried out to one order higher than in § 2.2. We will here briefly review the derivation of his result, with the aim of establishing the relationship to those derived above. Following the procedure outlined in § 2.2, but carried out to third order (see Reference Longuet-HigginsLH63 for details), (2.18) becomes
where ![]() $\mathcal {K}\equiv\langle \zeta ^4\rangle$ is the kurtosis. Reference Longuet-HigginsLH63 conceptually divided the integrand as
$\mathcal {K}\equiv\langle \zeta ^4\rangle$ is the kurtosis. Reference Longuet-HigginsLH63 conceptually divided the integrand as
and subsequently replaced the second exponential with its Taylor series. This leads to the approximation
After integrating, his final result takes the form of a Gram–Charlier series
where
are Hermite polynomials. Note that the term proportional to ![]() $\mathcal {S}$ is
$\mathcal {S}$ is ![]() $O(\varepsilon )$, whereas the terms within the curly braces are
$O(\varepsilon )$, whereas the terms within the curly braces are ![]() $O(\varepsilon ^2)$.
$O(\varepsilon ^2)$.
It is important to emphasize that (3.4) is only an approximation of (3.1), even to second order. The reason is that the Taylor series expansion introduced within the integrand of (3.3) will only be accurate for small ![]() $|s|$, and not over the entire interval
$|s|$, and not over the entire interval ![]() $-\infty \leqslant s\leqslant \infty$. As was mentioned in § 2.2, to second order the result of Reference Longuet-HigginsLH63 above, in fact, matches the p.d.f. derived from the moment generating function, rather than from the cumulant generating function on which it is based. It turns out that his final result is only asymptotic to our result given in (2.31).
$-\infty \leqslant s\leqslant \infty$. As was mentioned in § 2.2, to second order the result of Reference Longuet-HigginsLH63 above, in fact, matches the p.d.f. derived from the moment generating function, rather than from the cumulant generating function on which it is based. It turns out that his final result is only asymptotic to our result given in (2.31).
Comparison of the p.d.f.s given by (3.4) and the newly derived (2.31) are presented in figure 2, utilizing ![]() $\mathcal {S}=0.3$ and (for the third-order result of Reference Longuet-HigginsLH63)
$\mathcal {S}=0.3$ and (for the third-order result of Reference Longuet-HigginsLH63) ![]() $\mathcal {K}=3.1$. These values have been chosen to be reasonably representative of a typical nonlinear, irregular sea in intermediate depth to deep water, see e.g. figure 2 of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b), as well as in tables 1 and 2 (see § 6). It is seen that the present (second-order) method predicts increased probability density of extreme positive
$\mathcal {K}=3.1$. These values have been chosen to be reasonably representative of a typical nonlinear, irregular sea in intermediate depth to deep water, see e.g. figure 2 of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b), as well as in tables 1 and 2 (see § 6). It is seen that the present (second-order) method predicts increased probability density of extreme positive ![]() $\zeta$ relative to both the second- and third-order approaches of Reference Longuet-HigginsLH63. This heavy tail will be investigated and explained in the next section. It is likewise seen that all of the distributions shown suffer from non-physical oscillations for moderate to large, negative
$\zeta$ relative to both the second- and third-order approaches of Reference Longuet-HigginsLH63. This heavy tail will be investigated and explained in the next section. It is likewise seen that all of the distributions shown suffer from non-physical oscillations for moderate to large, negative ![]() $\zeta$. The failure in this region implies that these p.d.f.s cannot be utilized to reliably predict the probability density of the surface elevation in moderate to extreme wave trough regions. A semi-theoretical means of remedying this deficiency in (2.31) is developed in § 5.1, valid for weakly nonlinear situations having sufficiently small skewness.
$\zeta$. The failure in this region implies that these p.d.f.s cannot be utilized to reliably predict the probability density of the surface elevation in moderate to extreme wave trough regions. A semi-theoretical means of remedying this deficiency in (2.31) is developed in § 5.1, valid for weakly nonlinear situations having sufficiently small skewness.

Figure 2. Comparison of the p.d.f. from (2.31) (full line) with the second- (dashed line) and third-order (dotted line) approximations of Reference Longuet-HigginsLH63, from (3.4). All cases use ![]() $\mathcal {S}=0.30$, with the Reference Longuet-HigginsLH63 third-order result additionally using
$\mathcal {S}=0.30$, with the Reference Longuet-HigginsLH63 third-order result additionally using ![]() $\mathcal {K}=3.1$. Note the non-physical oscillations for
$\mathcal {K}=3.1$. Note the non-physical oscillations for ![]() $\zeta \lesssim -2.8$ exhibited by all three distributions.
$\zeta \lesssim -2.8$ exhibited by all three distributions.
Table 1. Summary statistics from the data generated using the second-order irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012). All cases utilize finite depth ![]() $k_ph=1.2$ and directional spreading parameter
$k_ph=1.2$ and directional spreading parameter ![]() $N_D=50$.
$N_D=50$.

Table 2. Summary statistics for the data generated from fully nonlinear numerical simulations. All cases utilize directional-spreading parameter ![]() $N_D=2$.
$N_D=2$.

4. Asymptotic limits of the p.d.f.s for large surface elevations
The example depicted in figure 2 demonstrates that the new second-order p.d.f. (2.31) has a heavier tail than both the second- and third-order results of Reference Longuet-HigginsLH63. This can be explained by inspection of their asymptotic forms for large surface elevations. As ![]() $\zeta \to \infty$, our new p.d.f. (2.31) tends asymptotically to
$\zeta \to \infty$, our new p.d.f. (2.31) tends asymptotically to
 \begin{equation} p(\zeta)\sim \frac{1}{2^{3/4}\sqrt{\rm \pi}(\mathcal{S}\zeta)^{1/4}} \exp\left( \frac{1}{3\mathcal{S}^2} - \frac{1}{8\sqrt{2\zeta}\mathcal{S}^{5/2}} - \frac{\sqrt{\zeta}}{\sqrt{2}\mathcal{S}^{3/2}} + \frac{\zeta}{\mathcal{S}} - \frac{2\sqrt{2}\zeta^{3/2}}{3\sqrt{\mathcal{S}}} \right). \end{equation}
\begin{equation} p(\zeta)\sim \frac{1}{2^{3/4}\sqrt{\rm \pi}(\mathcal{S}\zeta)^{1/4}} \exp\left( \frac{1}{3\mathcal{S}^2} - \frac{1}{8\sqrt{2\zeta}\mathcal{S}^{5/2}} - \frac{\sqrt{\zeta}}{\sqrt{2}\mathcal{S}^{3/2}} + \frac{\zeta}{\mathcal{S}} - \frac{2\sqrt{2}\zeta^{3/2}}{3\sqrt{\mathcal{S}}} \right). \end{equation}Conversely, the second- and third-order p.d.f.s of Reference Longuet-HigginsLH63 (see present (3.4)), respectively, tend asymptotically to
and
These asymptotic forms are plotted in figure 3, along with the Gaussian distribution (2.39). For consistency with figure 2, with the exception of the Gaussian distribution, all cases use ![]() $\mathcal {S}=0.3$. Note that the asymptotic form of the third-order Reference Longuet-HigginsLH63 result (4.3) involves
$\mathcal {S}=0.3$. Note that the asymptotic form of the third-order Reference Longuet-HigginsLH63 result (4.3) involves ![]() $\mathcal {S}^2$, and not
$\mathcal {S}^2$, and not ![]() $\mathcal {K}$. Notice that the asymptotic forms stemming from Reference Longuet-HigginsLH63's result, (4.2) and (4.3), are merely factors of
$\mathcal {K}$. Notice that the asymptotic forms stemming from Reference Longuet-HigginsLH63's result, (4.2) and (4.3), are merely factors of ![]() $\mathcal {S}\zeta ^3/6$ and
$\mathcal {S}\zeta ^3/6$ and ![]() $\mathcal {S}^2\zeta ^6/72$ times the Gaussian distribution (2.39), both having argument
$\mathcal {S}^2\zeta ^6/72$ times the Gaussian distribution (2.39), both having argument ![]() $-\zeta ^2/2$ in the exponential function. As these match that of the Gaussian distribution, their positive tails are likewise similar, essentially being just vertically shifted when plotted on semi-logarithmic axes. Conversely, the asymptotic limit of the present new p.d.f. is fundamentally different. In particular, it is noted that all powers of
$-\zeta ^2/2$ in the exponential function. As these match that of the Gaussian distribution, their positive tails are likewise similar, essentially being just vertically shifted when plotted on semi-logarithmic axes. Conversely, the asymptotic limit of the present new p.d.f. is fundamentally different. In particular, it is noted that all powers of ![]() $\zeta$ within the argument of the exponential function in (4.1) are less than the power
$\zeta$ within the argument of the exponential function in (4.1) are less than the power ![]() $2$ of the Gaussian distribution, the largest power being
$2$ of the Gaussian distribution, the largest power being ![]() $3/2$. This explains the heavier positive tail exhibited by the present new p.d.f. (2.31), relative to those of Reference Longuet-HigginsLH63 from (3.4).
$3/2$. This explains the heavier positive tail exhibited by the present new p.d.f. (2.31), relative to those of Reference Longuet-HigginsLH63 from (3.4).

Figure 3. Comparison of the asymptotic forms (as ![]() $\zeta \to \infty$) of the p.d.f.s. Lines correspond to the present second-order theory (4.1) (full line), the second- (4.2) (dashed line) and third-order (4.3) (dotted line) approximations of Reference Longuet-HigginsLH63, as well as the Gaussian distribution (2.39) (dashed-dotted line). With the exception of the Gaussian distribution, all cases use
$\zeta \to \infty$) of the p.d.f.s. Lines correspond to the present second-order theory (4.1) (full line), the second- (4.2) (dashed line) and third-order (4.3) (dotted line) approximations of Reference Longuet-HigginsLH63, as well as the Gaussian distribution (2.39) (dashed-dotted line). With the exception of the Gaussian distribution, all cases use ![]() $\mathcal {S}=0.30$. Note the heavy tail exhibited by the present distribution (full line).
$\mathcal {S}=0.30$. Note the heavy tail exhibited by the present distribution (full line).
It is emphasized that the heavy tail, and any associated increased accuracy (see forthcoming § 6), exhibited by the present second-order p.d.f., relative e.g. even to the third-order result of Reference Longuet-HigginsLH63, would not be in violation of any theory. The formal order of a given method only governs its asymptotic rate of convergence in the limit of small steepness; higher formal order does not necessarily imply greater accuracy. Indeed, as shown in § 2.3, the differences between the new second-order p.d.f. (2.31) and the second-order result of Reference Longuet-HigginsLH63, which again matches (2.13), are themselves of third order. This section establishes that a heavy tail is inherent within the new second-order p.d.f. (2.31) and is among these differences.
5. Practical considerations
5.1. Removal of spurious oscillations in the negative tail
As shown in figure 2 (full line), for finite ![]() $\mathcal {S}$ and moderate to large, negative
$\mathcal {S}$ and moderate to large, negative ![]() $\zeta$, the p.d.f. given in (2.31) results in spurious oscillations, and even negative probability densities. Such features can obviously be dismissed as non-physical. A semi-theoretical method for addressing the oscillations inherent in (2.31), valid for small but finite
$\zeta$, the p.d.f. given in (2.31) results in spurious oscillations, and even negative probability densities. Such features can obviously be dismissed as non-physical. A semi-theoretical method for addressing the oscillations inherent in (2.31), valid for small but finite ![]() $\mathcal {S}$, will be developed in the present section, inspired by inspection of the Airy functions with negative arguments. For later use within this section, note that the Airy function of the second kind is defined by
$\mathcal {S}$, will be developed in the present section, inspired by inspection of the Airy functions with negative arguments. For later use within this section, note that the Airy function of the second kind is defined by
To begin, both ![]() $\text {Ai}(\chi )$ (grey dashed line) and
$\text {Ai}(\chi )$ (grey dashed line) and ![]() $\text {Bi}(\chi )$ (grey dotted line) are plotted in figure 4. It is additionally noted that the envelope of both Airy functions (with negative arguments) follows
$\text {Bi}(\chi )$ (grey dotted line) are plotted in figure 4. It is additionally noted that the envelope of both Airy functions (with negative arguments) follows
which is depicted as the full line in figure 4. The asymptotic limit as ![]() $\chi \to -\infty$,
$\chi \to -\infty$, ![]() $\mbox {Ci}(\chi )\sim {\rm \pi}^{-1/2}(-\chi )^{-1/4}$, is also shown for completeness.
$\mbox {Ci}(\chi )\sim {\rm \pi}^{-1/2}(-\chi )^{-1/4}$, is also shown for completeness.

Figure 4. Plot demonstrating the behaviour of the Airy functions ![]() $\text {Ai}(\chi )$ and
$\text {Ai}(\chi )$ and ![]() $\text {Bi}(\chi )$, their envelope
$\text {Bi}(\chi )$, their envelope ![]() $\mbox {Ci}(\chi )$ as well as its asymptotic form
$\mbox {Ci}(\chi )$ as well as its asymptotic form ![]() $\mbox{Ci}(\chi)\sim{\rm \pi}^{-1/2}(-\chi)^{-1/4}$.
$\mbox{Ci}(\chi)\sim{\rm \pi}^{-1/2}(-\chi)^{-1/4}$.
Inspired by the observations above, we propose the following as a suitable generalization of (2.31) for some practical purposes:
 \begin{equation} p(\zeta)= \left(\frac{2}{\mathcal{S}}\right)^{1/3} \exp\left[\frac{1}{3\mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right] \mbox{Zi}\left(\chi\right), \end{equation}
\begin{equation} p(\zeta)= \left(\frac{2}{\mathcal{S}}\right)^{1/3} \exp\left[\frac{1}{3\mathcal{S}^2} + \frac{\zeta}{\mathcal{S}}\right] \mbox{Zi}\left(\chi\right), \end{equation}
wherein ![]() $\text {Ai}(\chi )$ has been replaced with
$\text {Ai}(\chi )$ has been replaced with
 \begin{equation} \mbox{Zi}(\chi)\equiv \begin{cases} \text{Ai}(\chi) & \text{for} \ \chi\geqslant\chi_0 \\ \mbox{Ci}(\chi) & \text{for} \ \chi<\chi_0. \end{cases}\end{equation}
\begin{equation} \mbox{Zi}(\chi)\equiv \begin{cases} \text{Ai}(\chi) & \text{for} \ \chi\geqslant\chi_0 \\ \mbox{Ci}(\chi) & \text{for} \ \chi<\chi_0. \end{cases}\end{equation}
To ensure smoothness of the modified p.d.f., we require that ![]() $\text {Ai}(\chi _0)=\mbox {Ci}(\chi _0)$ and
$\text {Ai}(\chi _0)=\mbox {Ci}(\chi _0)$ and ![]() $\text {Ai}^\prime (\chi _0)=\mbox {Ci}^\prime (\chi _0)$, both of which are satisfied at
$\text {Ai}^\prime (\chi _0)=\mbox {Ci}^\prime (\chi _0)$, both of which are satisfied at ![]() $\chi _0\approx -1.17371$, see figure 4. The modification above enables direct use of the
$\chi _0\approx -1.17371$, see figure 4. The modification above enables direct use of the ![]() $\text {Ai}(\chi )$ function for
$\text {Ai}(\chi )$ function for ![]() $\chi \geqslant \chi _0$, fully consistent with the theory from (2.31). Conversely, it switches to the envelope
$\chi \geqslant \chi _0$, fully consistent with the theory from (2.31). Conversely, it switches to the envelope ![]() $\mbox {Ci}(\chi )$ for
$\mbox {Ci}(\chi )$ for ![]() $\chi <\chi _0$, where the theoretical solution clearly breaks down.
$\chi <\chi _0$, where the theoretical solution clearly breaks down.
To check the practical validity of (5.3), we plot the integral of the resulting p.d.f., as well as its first four statistical moments, vs the input skewness ![]() $\mathcal {S}$ in figure 5. All plotted quantities are thus of the general form
$\mathcal {S}$ in figure 5. All plotted quantities are thus of the general form
where ![]() $m=0, 1, \ldots, 4$, where each is normalized and/or vertically shifted as indicated in the figure legend, such that they should theoretically be equal to zero. It is seen that for all quantities plotted reasonable accuracy is maintained for say
$m=0, 1, \ldots, 4$, where each is normalized and/or vertically shifted as indicated in the figure legend, such that they should theoretically be equal to zero. It is seen that for all quantities plotted reasonable accuracy is maintained for say ![]() $\mathcal {S}\lesssim 0.2$. At the upper limit
$\mathcal {S}\lesssim 0.2$. At the upper limit ![]() $\mathcal {S}=0.2$ the modified p.d.f. from (5.3) yields a mean of
$\mathcal {S}=0.2$ the modified p.d.f. from (5.3) yields a mean of ![]() $-0.00015$, a variance of 1.0005, a skewness of 0.199 and a kurtosis of 3.007. These may be compared with their respective theoretical values of zero, unity, 0.2 (as input) and 3. It is emphasized that if the theoretical p.d.f. from (2.31) is maintained then the theoretical values are matched exactly, regardless of
$-0.00015$, a variance of 1.0005, a skewness of 0.199 and a kurtosis of 3.007. These may be compared with their respective theoretical values of zero, unity, 0.2 (as input) and 3. It is emphasized that if the theoretical p.d.f. from (2.31) is maintained then the theoretical values are matched exactly, regardless of ![]() $\mathcal {S}$.
$\mathcal {S}$.

Figure 5. Integral and statistical moments computed from the modified p.d.f. (5.3). All integrals have been shifted and/or normalized as indicated in the legend, such that plotted quantities should theoretically be zero.
An example using the modified p.d.f. defined in (5.3), now with ![]() $\mathcal {S}=0.2$ (again, the upper recommended limit), can be seen as the full black line in figure 6. This result can be compared with the previously discussed result based on (2.31), which is similarly plotted as the grey dashed line in figure 6. It is seen that the two are, by design, identical for positive and moderately negative
$\mathcal {S}=0.2$ (again, the upper recommended limit), can be seen as the full black line in figure 6. This result can be compared with the previously discussed result based on (2.31), which is similarly plotted as the grey dashed line in figure 6. It is seen that the two are, by design, identical for positive and moderately negative ![]() $\zeta$. Importantly, (5.3) avoids any spurious non-physical oscillations for negative
$\zeta$. Importantly, (5.3) avoids any spurious non-physical oscillations for negative ![]() $\zeta$, which are erroneously exhibited by (2.31).
$\zeta$, which are erroneously exhibited by (2.31).
To conclude: the theoretically derived new second-order p.d.f. corresponds to (2.31). Should it be desired, for weakly nonlinear cases having ![]() $\mathcal {S}\leqslant 0.2$, this may be replaced in practice with (5.3), which will remove spurious oscillations of the negative tail, while maintaining reasonably accurate statistical moments. The accuracy of the resulting p.d.f.s will be directly tested in § 6, where the limits in
$\mathcal {S}\leqslant 0.2$, this may be replaced in practice with (5.3), which will remove spurious oscillations of the negative tail, while maintaining reasonably accurate statistical moments. The accuracy of the resulting p.d.f.s will be directly tested in § 6, where the limits in ![]() $\mathcal {S}$ suggested above will be strictly followed.
$\mathcal {S}$ suggested above will be strictly followed.
5.2. Numerical precision
Regarding practical issues, it should be finally mentioned that the evaluation of ![]() $\text {Ai}(\chi )$ can face problems associated with loss of numerical precision, particularly when considering cases having small
$\text {Ai}(\chi )$ can face problems associated with loss of numerical precision, particularly when considering cases having small ![]() $\mathcal {S}$. When making calculations in double precision we find that such issues can arise whenever this argument becomes
$\mathcal {S}$. When making calculations in double precision we find that such issues can arise whenever this argument becomes ![]() $\chi >\chi _{thresh}\approx 108$, which will return zero, rather than an extremely small number (which in turn must be multiplied by an extremely large number stemming from the exponential function, see (2.31) or (5.3)). From the definition in (2.22), this issue will manifest in
$\chi >\chi _{thresh}\approx 108$, which will return zero, rather than an extremely small number (which in turn must be multiplied by an extremely large number stemming from the exponential function, see (2.31) or (5.3)). From the definition in (2.22), this issue will manifest in ![]() $p(\zeta )$ whenever
$p(\zeta )$ whenever
Fortunately, this issue is easily overcome in practice simply by ensuring that the argument ![]() $\chi$ is evaluated to high precision e.g. using vpi in Matlab or SetPrecision in Mathematica, and we recommend doing similarly for the argument of the exponential function for the sake of consistency. Such high-precision calculations have been utilized in all relevant plots presented throughout the present work. As an example implementation, a Matlab function pdfAiry.m evaluating the p.d.f. defined in (5.3) if
$\chi$ is evaluated to high precision e.g. using vpi in Matlab or SetPrecision in Mathematica, and we recommend doing similarly for the argument of the exponential function for the sake of consistency. Such high-precision calculations have been utilized in all relevant plots presented throughout the present work. As an example implementation, a Matlab function pdfAiry.m evaluating the p.d.f. defined in (5.3) if ![]() $\mathcal {S}\leqslant 0.2$ and (2.31) otherwise is provided at the link indicated in the Data Availability section towards the end of the present paper.
$\mathcal {S}\leqslant 0.2$ and (2.31) otherwise is provided at the link indicated in the Data Availability section towards the end of the present paper.
6. Comparisons
6.1. Comparison with results from second-order irregular wave theory
As a first means of validation we will compare the new p.d.f.s against those generated from time series utilizing the directionally spread (third-order) irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012), carried out to second order. (Note that some errors unfortunately appeared in their original publication, which are pointed out for clarity in Appendix A.) For validation purposes we will consider three cases, each based on a Joint North Sea Wave Project (JONSWAP) spectrum (Hasselmann et al. Reference Hasselmann1973)
 \begin{equation} S(\omega)=S_0\left(\frac{\omega}{\omega_p}\right)^{-5} \exp\Bigg(-\frac{5}{4}\left(\frac{\omega}{\omega_p}\right)^{-4}\Bigg)\gamma_s^{\exp\left(-(\omega/\omega_p-1)^2/(2\sigma_s^2)\right)}, \end{equation}
\begin{equation} S(\omega)=S_0\left(\frac{\omega}{\omega_p}\right)^{-5} \exp\Bigg(-\frac{5}{4}\left(\frac{\omega}{\omega_p}\right)^{-4}\Bigg)\gamma_s^{\exp\left(-(\omega/\omega_p-1)^2/(2\sigma_s^2)\right)}, \end{equation}
where ![]() $\omega$ is the angular frequency,
$\omega$ is the angular frequency, ![]() $\omega _p$ is the peak angular frequency,
$\omega _p$ is the peak angular frequency, ![]() $\gamma _s=3.3$ and
$\gamma _s=3.3$ and ![]() $\sigma _s=0.07$ if
$\sigma _s=0.07$ if ![]() $\omega <\omega _p$ and 0.09 otherwise. A cutoff frequency of
$\omega <\omega _p$ and 0.09 otherwise. A cutoff frequency of ![]() $\omega _{c}=3\omega _p$ is utilized, such that
$\omega _{c}=3\omega _p$ is utilized, such that ![]() $S(\omega >\omega _{c})=0$. The constant
$S(\omega >\omega _{c})=0$. The constant ![]() $S_0$ is defined such that the linearized spectrum satisfies
$S_0$ is defined such that the linearized spectrum satisfies
with second-order components added afterwards. The waves are directionally spread (utilizing single summation) based on
 \begin{equation} D(\theta)= \begin{cases} \dfrac{\varGamma(N_D/2+1)}{\sqrt{\rm \pi}(\varGamma(N_D+1)/2)} \cos^{N_D}(\theta) & \text{if} \ |\theta|\leqslant\dfrac{\rm \pi}{2} \\[10pt] 0 & \text{otherwise}, \end{cases} \end{equation}
\begin{equation} D(\theta)= \begin{cases} \dfrac{\varGamma(N_D/2+1)}{\sqrt{\rm \pi}(\varGamma(N_D+1)/2)} \cos^{N_D}(\theta) & \text{if} \ |\theta|\leqslant\dfrac{\rm \pi}{2} \\[10pt] 0 & \text{otherwise}, \end{cases} \end{equation}
where ![]() $\varGamma ({\cdot })$ denotes the gamma function and
$\varGamma ({\cdot })$ denotes the gamma function and ![]() $N_D$ is the directional-spreading parameter, which governs the width of the directional spectrum.
$N_D$ is the directional-spreading parameter, which governs the width of the directional spectrum.
All cases utilize a finite depth such that ![]() $k_ph=1.2$, where
$k_ph=1.2$, where ![]() $k_p$ is the peak wavenumber, determined from the dispersion relation
$k_p$ is the peak wavenumber, determined from the dispersion relation
and ![]() $h=70$ m is the water depth, with gravitational acceleration
$h=70$ m is the water depth, with gravitational acceleration ![]() $g=9.81\ {\rm m}\ {\rm s}^{-2}$ such that the peak period is
$g=9.81\ {\rm m}\ {\rm s}^{-2}$ such that the peak period is ![]() $T_p=16.8$ s. All cases utilize the directional-spreading parameter
$T_p=16.8$ s. All cases utilize the directional-spreading parameter ![]() $N_D=50$. We will consider three cases representing storm conditions with linear steepness
$N_D=50$. We will consider three cases representing storm conditions with linear steepness ![]() $\varepsilon =k_pH_{m0}/2=2k_p\sigma =0.10$,
$\varepsilon =k_pH_{m0}/2=2k_p\sigma =0.10$, ![]() $0.15$ and
$0.15$ and ![]() $0.20$, where
$0.20$, where ![]() $H_{m0}$ is the spectral significant wave height. The primary purpose of the present comparisons is thus to test the performance of the new p.d.f.s for irregular wave fields having variable nonlinearity in finite depth. For each case numerous (
$H_{m0}$ is the spectral significant wave height. The primary purpose of the present comparisons is thus to test the performance of the new p.d.f.s for irregular wave fields having variable nonlinearity in finite depth. For each case numerous (![]() ${\approx }120\,000$) discrete time series segments have been independently generated, each spanning a duration
${\approx }120\,000$) discrete time series segments have been independently generated, each spanning a duration ![]() $100T_p$, resolved with time step
$100T_p$, resolved with time step ![]() $\Delta t=T_p/20$. This means that, for each condition considered, approximately
$\Delta t=T_p/20$. This means that, for each condition considered, approximately ![]() $6.4$ years of storm data are collectively generated and analysed. The resulting statistics (steepness
$6.4$ years of storm data are collectively generated and analysed. The resulting statistics (steepness ![]() $\varepsilon$, variance
$\varepsilon$, variance ![]() $\sigma ^2$, skewness
$\sigma ^2$, skewness ![]() $\mathcal {S}$ and kurtosis
$\mathcal {S}$ and kurtosis ![]() $\mathcal {K}$) are summarized in table 1.
$\mathcal {K}$) are summarized in table 1.
Selected time series segments are exemplified in figure 7, corresponding to those containing the largest crest elevation generated for each case. Insets are provided on each panel, depicting a zoomed-in region surrounding the large crests. It is seen that these selected events contain isolated rogue waves, with crest elevations in the most extreme case generated reaching nearly ![]() $\zeta =8$. Interestingly, these extreme events are typically surrounded by otherwise rather ordinary conditions for the sea states considered, typically with
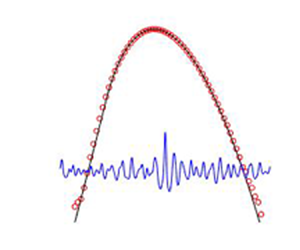
$\zeta =8$. Interestingly, these extreme events are typically surrounded by otherwise rather ordinary conditions for the sea states considered, typically with ![]() $-3\leqslant \zeta \leqslant 3$. That the extreme waves would appear to have ‘come from nowhere’ seems consistent with anecdotal accounts often reported by mariners and as occasionally even measured. Note e.g. the qualitative similarity with the famous ‘New Year’ rogue wave, measured in the North Sea on 1 January 1995 from the Draupner oil platform (water depth
$-3\leqslant \zeta \leqslant 3$. That the extreme waves would appear to have ‘come from nowhere’ seems consistent with anecdotal accounts often reported by mariners and as occasionally even measured. Note e.g. the qualitative similarity with the famous ‘New Year’ rogue wave, measured in the North Sea on 1 January 1995 from the Draupner oil platform (water depth ![]() $h=70$ m), similarly presented in figure 8. Based on analysis of this measured time series segment alone, the storm conditions there would correspond to
$h=70$ m), similarly presented in figure 8. Based on analysis of this measured time series segment alone, the storm conditions there would correspond to ![]() $\sigma ^2\approx 8.9\ {\rm m}^2$,
$\sigma ^2\approx 8.9\ {\rm m}^2$, ![]() $k_ph\approx 1.2$ and
$k_ph\approx 1.2$ and ![]() $\varepsilon \approx 0.10$, similar to the input conditions leading to the event depicted in figure 7(a). (The close similarity in input for this case is intentional, as we were curious to see if similar peak events might indeed be generated stochastically using a second-order theory.)
$\varepsilon \approx 0.10$, similar to the input conditions leading to the event depicted in figure 7(a). (The close similarity in input for this case is intentional, as we were curious to see if similar peak events might indeed be generated stochastically using a second-order theory.)

Figure 7. Example time series involving the largest crests (occurring at time ![]() $t=t_p$) generated by the irregular, directionally spread wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012) to second order. Insets depicting the region immediately surrounding the largest crest are added on each panel. Cases utilize
$t=t_p$) generated by the irregular, directionally spread wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012) to second order. Insets depicting the region immediately surrounding the largest crest are added on each panel. Cases utilize ![]() $k_ph=1.2$ and
$k_ph=1.2$ and ![]() $N_D=50$ coupled with linear steepness (a)
$N_D=50$ coupled with linear steepness (a) ![]() $\varepsilon =0.10$, (b) 0.15 and (c) 0.20.
$\varepsilon =0.10$, (b) 0.15 and (c) 0.20.

Figure 8. Time series segment containing the famous ‘New Year’ rogue wave measured from the Draupner oil platform in the North Sea on 1 January 1995.
For each case the numerous time series segments have been collectively analysed, with a ![]() $\zeta$ bin size corresponding to
$\zeta$ bin size corresponding to ![]() $0.2$, resulting in the three p.d.f.s (circles) shown in figure 9. Error bars are also included, estimated as
$0.2$, resulting in the three p.d.f.s (circles) shown in figure 9. Error bars are also included, estimated as ![]() $\pm p(\zeta )/\sqrt {N_b}$, where
$\pm p(\zeta )/\sqrt {N_b}$, where ![]() $N_b$ is the number of samples in each bin, following Onorato et al. (Reference Onorato2009). Also shown for comparison are the p.d.f.s from (i) the Gaussian distribution (dotted lines), (ii) Reference Longuet-HigginsLH63 (second order: dashed lines, third order: dashed-dotted lines) and (iii) the presently proposed p.d.f.s (full lines). In line with the recommendation made in § 5.1, the modified variant (5.3) is only utilized in the case where
$N_b$ is the number of samples in each bin, following Onorato et al. (Reference Onorato2009). Also shown for comparison are the p.d.f.s from (i) the Gaussian distribution (dotted lines), (ii) Reference Longuet-HigginsLH63 (second order: dashed lines, third order: dashed-dotted lines) and (iii) the presently proposed p.d.f.s (full lines). In line with the recommendation made in § 5.1, the modified variant (5.3) is only utilized in the case where ![]() $\mathcal {S}\leqslant 0.2$ (figure 9a), whereas the theoretical p.d.f. (2.31) is utilized in figure 9(b,c). It is seen that the proposed new p.d.f. provides superior accuracy to both the Gaussian distributions (expected from linear theory), as well as those of Reference Longuet-HigginsLH63, especially in the positive tail. Somewhat remarkably, and as mentioned previously, even though effects of kurtosis are not at all accounted for, the present distribution even outperforms the third-order distribution of Reference Longuet-HigginsLH63. As should be expected from § 5.1, the distribution from (5.3) (figure 9a) is free of spurious oscillations in the negative tail, in contrast to those of Reference Longuet-HigginsLH63 or (2.31) which fail for roughly
$\mathcal {S}\leqslant 0.2$ (figure 9a), whereas the theoretical p.d.f. (2.31) is utilized in figure 9(b,c). It is seen that the proposed new p.d.f. provides superior accuracy to both the Gaussian distributions (expected from linear theory), as well as those of Reference Longuet-HigginsLH63, especially in the positive tail. Somewhat remarkably, and as mentioned previously, even though effects of kurtosis are not at all accounted for, the present distribution even outperforms the third-order distribution of Reference Longuet-HigginsLH63. As should be expected from § 5.1, the distribution from (5.3) (figure 9a) is free of spurious oscillations in the negative tail, in contrast to those of Reference Longuet-HigginsLH63 or (2.31) which fail for roughly ![]() $\zeta <-3$. The comparison in figure 9(a) suggests that this modification provides similar accuracy for predicting the probability density of negative surface elevations as for positive ones, at least for cases having
$\zeta <-3$. The comparison in figure 9(a) suggests that this modification provides similar accuracy for predicting the probability density of negative surface elevations as for positive ones, at least for cases having ![]() $\mathcal {S}\leqslant 0.2$ where it can be reasonably applied. Remaining differences between the generated data and the new p.d.f.s seem likely due to neglected third-order effects in the distribution (e.g. kurtosis). Obviously, none of the methods employed account for any effects of wave breaking on the p.d.f., although there is considerable evidence that these do not necessarily have a significant impact in the probability domain, see e.g. the discussion in Tayfun & Alkhalidi (Reference Tayfun and Alkhalidi2020).
$\mathcal {S}\leqslant 0.2$ where it can be reasonably applied. Remaining differences between the generated data and the new p.d.f.s seem likely due to neglected third-order effects in the distribution (e.g. kurtosis). Obviously, none of the methods employed account for any effects of wave breaking on the p.d.f., although there is considerable evidence that these do not necessarily have a significant impact in the probability domain, see e.g. the discussion in Tayfun & Alkhalidi (Reference Tayfun and Alkhalidi2020).

Figure 9. Comparison of p.d.f.s computed from the second-order directionally spread irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012, referred to as MF12) (circles, with error bars) with (3.4) from Reference Longuet-HigginsLH63 (second order, dashed lines; third order, dashed-dotted lines) and the present work using (a) (5.3) and (b,c) (2.31) (full lines). Cases utilize ![]() $k_ph=1.2$ and
$k_ph=1.2$ and ![]() $N_D=50$ coupled with (a)
$N_D=50$ coupled with (a) ![]() $\varepsilon =0.1007$, (b) 0.1524 and (c) 0.2057, with other statistical quantities given in table 1.
$\varepsilon =0.1007$, (b) 0.1524 and (c) 0.2057, with other statistical quantities given in table 1.
6.2. Comparison with results from fully nonlinear numerical simulations
As an additional means of validation, we will consider data generated utilizing the fully nonlinear pseudospectral Fourier–Legendre (PFL) potential flow simulation model of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021c), as used previously by Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb). This model is spectrally accurate in all three spatial directions and maintains good computational efficiency. This method makes use of an artificial lower boundary condition based on Nicholls (Reference Nicholls2011), with iterative solutions to the resulting Laplace equation utilizing a linearized preconditioner, following the strategy of Fuhrman & Bingham (Reference Fuhrman and Bingham2004). For full details on this model and features, see Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb,Reference Klahn, Madsen and Fuhrmanc).
We simulate irregular, directionally spread wave fields, again based on JONSWAP spectra, with ![]() $k_ph=1.0$,
$k_ph=1.0$, ![]() $1.5$ and
$1.5$ and ![]() $\infty$ (deep water), now utilizing the directional-spreading parameter
$\infty$ (deep water), now utilizing the directional-spreading parameter ![]() $N_D=2$. For all cases simulations utilize a large
$N_D=2$. For all cases simulations utilize a large ![]() $2048\times 2048$ (horizontal) grid, coupled with
$2048\times 2048$ (horizontal) grid, coupled with ![]() $11$ points distributed in the vertical direction. The computational domain has lengths
$11$ points distributed in the vertical direction. The computational domain has lengths ![]() $L_x=100\lambda _p$ and
$L_x=100\lambda _p$ and ![]() $L_y=100(1+N_D)^{1/2}\lambda _p$, where
$L_y=100(1+N_D)^{1/2}\lambda _p$, where ![]() $\lambda _p=2{\rm \pi} /k_p=275$ m, which provides similar resolution of wavelengths in both horizontal directions, following Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a). Note that the resolution utilized implies that the spectrum is effectively cut off at
$\lambda _p=2{\rm \pi} /k_p=275$ m, which provides similar resolution of wavelengths in both horizontal directions, following Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a). Note that the resolution utilized implies that the spectrum is effectively cut off at ![]() $\omega _{c}\approx 4.86\omega _p$, see (3.24) of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a). The computational domains can be considered extremely large for such fully nonlinear simulations, covering a physical area corresponding to
$\omega _{c}\approx 4.86\omega _p$, see (3.24) of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a). The computational domains can be considered extremely large for such fully nonlinear simulations, covering a physical area corresponding to ![]() $28.2\ {\rm km} \times 48.8\ {\rm km}$. Starting with linearized initial conditions, the nonlinear terms are ramped to fully on over a duration of
$28.2\ {\rm km} \times 48.8\ {\rm km}$. Starting with linearized initial conditions, the nonlinear terms are ramped to fully on over a duration of ![]() $10T_p$, following the same procedure described in Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb), and then continued for a total duration of
$10T_p$, following the same procedure described in Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb), and then continued for a total duration of ![]() $100T_p$. The characteristic wave steepness for the linearized initial conditions are set according to
$100T_p$. The characteristic wave steepness for the linearized initial conditions are set according to ![]() $\varepsilon = \varepsilon _0\tanh (0.8863k_ph)$, where
$\varepsilon = \varepsilon _0\tanh (0.8863k_ph)$, where ![]() $\varepsilon _0 = 0.15$ is a deep water ‘equivalent steepness’. This ensures that, for a given
$\varepsilon _0 = 0.15$ is a deep water ‘equivalent steepness’. This ensures that, for a given ![]() $\varepsilon _0$, cases in any
$\varepsilon _0$, cases in any ![]() $k_ph$ will have roughly the same degree of nonlinearity, relative to the maximum steepness criterion of Battjes (Reference Battjes1974). The primary purpose of the present tests is thus to compare the performance of the new p.d.f.s in irregular wave fields having similar nonlinearity, but with variable dimensionless water depth. Note that above the steepness
$k_ph$ will have roughly the same degree of nonlinearity, relative to the maximum steepness criterion of Battjes (Reference Battjes1974). The primary purpose of the present tests is thus to compare the performance of the new p.d.f.s in irregular wave fields having similar nonlinearity, but with variable dimensionless water depth. Note that above the steepness ![]() $\varepsilon _0=0.15$ it becomes difficult to maintain stable nonlinear statistics, as shown e.g. in figure 2(a) of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b). This is due to dissipative effects introduced through filtering, which is necessary for stability purposes when extremely steep (potentially breaking) waves are encountered. The time step is set such that
$\varepsilon _0=0.15$ it becomes difficult to maintain stable nonlinear statistics, as shown e.g. in figure 2(a) of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b). This is due to dissipative effects introduced through filtering, which is necessary for stability purposes when extremely steep (potentially breaking) waves are encountered. The time step is set such that ![]() $\Delta t=T_p/50$. For each case, we have carried out the time integration with five different initial conditions, with the phase of each wave component determined randomly. Each simulation considered requires several months of simulation time on a single processor. The resulting statistics (steepness
$\Delta t=T_p/50$. For each case, we have carried out the time integration with five different initial conditions, with the phase of each wave component determined randomly. Each simulation considered requires several months of simulation time on a single processor. The resulting statistics (steepness ![]() $\varepsilon$, variance
$\varepsilon$, variance ![]() $\sigma ^2$, skewness
$\sigma ^2$, skewness ![]() $\mathcal {S}$ and kurtosis
$\mathcal {S}$ and kurtosis ![]() $\mathcal {K}$), based on data accumulated from all five simulations of each case at time
$\mathcal {K}$), based on data accumulated from all five simulations of each case at time ![]() $t=50T_p$, are summarized in table 2. Note that at this time the nonlinear wave fields can be considered well developed, with reasonably stable statistics, as established in previous simulations performed by Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb).
$t=50T_p$, are summarized in table 2. Note that at this time the nonlinear wave fields can be considered well developed, with reasonably stable statistics, as established in previous simulations performed by Klahn et al. (Reference Klahn, Madsen and Fuhrman2021a,Reference Klahn, Madsen and Fuhrmanb).
An example snapshot of the computational line in ![]() $x$ containing the largest rogue wave peak elevation generated at time
$x$ containing the largest rogue wave peak elevation generated at time ![]() $t=50T_p$ from the simulated case with
$t=50T_p$ from the simulated case with ![]() $k_ph=1.5$ is depicted in figure 10. Reasonable similarity with the time series from figures 7(a) and 8 can be there observed, with the free surface again reaching
$k_ph=1.5$ is depicted in figure 10. Reasonable similarity with the time series from figures 7(a) and 8 can be there observed, with the free surface again reaching ![]() $\zeta \approx 6$. A small three-dimensional segment of the simulated large domain containing this rogue wave is likewise provided in figure 11, as an example.
$\zeta \approx 6$. A small three-dimensional segment of the simulated large domain containing this rogue wave is likewise provided in figure 11, as an example.

Figure 10. Example free surface elevation along the line containing the largest crest generated by the fully nonlinear wave model of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021c) for the case with ![]() $k_ph=1.5$,
$k_ph=1.5$, ![]() $N_D=2$ and
$N_D=2$ and ![]() $\varepsilon =0.1270$. The inset depicts a zoomed-in region immediately surrounding the largest crest. Variable
$\varepsilon =0.1270$. The inset depicts a zoomed-in region immediately surrounding the largest crest. Variable ![]() $x_p$ denotes the
$x_p$ denotes the ![]() $x$ position of the highest crest peak.
$x$ position of the highest crest peak.

Figure 11. Snapshot of the surface elevation in the vicinity of the largest rogue wave crest generated by the fully nonlinear model of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021c) for the case with ![]() $k_ph=1.5$,
$k_ph=1.5$, ![]() $N_D=2$ and
$N_D=2$ and ![]() $\varepsilon =0.1270$. The horizontal axes are to scale, whereas the vertical axis is exaggerated by a factor of two. The horizontal area shown is
$\varepsilon =0.1270$. The horizontal axes are to scale, whereas the vertical axis is exaggerated by a factor of two. The horizontal area shown is ![]() $4\lambda _p\times 4\lambda _p$.
$4\lambda _p\times 4\lambda _p$.
The resulting p.d.f.s for the surface elevations accumulated from the fully nonlinear simulations for all three cases are presented as circles (with error bars, computed as previously described) in figure 12. For each case considered it is seen that isolated rogue waves having surface elevations reaching up to the previously mentioned ![]() $\zeta \approx 6$ have been generated in each case. As references the Gaussian distribution, as well as those from Reference Longuet-HigginsLH63 (both second and third order) are additionally shown in this figure. Good accuracy is confirmed with the present method utilizing (2.31) (figure 12a) and (5.3) (figure 12b,c as
$\zeta \approx 6$ have been generated in each case. As references the Gaussian distribution, as well as those from Reference Longuet-HigginsLH63 (both second and third order) are additionally shown in this figure. Good accuracy is confirmed with the present method utilizing (2.31) (figure 12a) and (5.3) (figure 12b,c as ![]() $\mathcal {S}\leqslant 0.2$) (full lines). The heavy positive tail associated with the present method is again evident, and is closer to the data than even the third-order distribution of Reference Longuet-HigginsLH63. In cases where the modified variant (5.3) has been utilized (again, figure 12b,c) oscillations in the negative tails are removed and the result matches the data reasonably. Based on these comparisons, it seems that the new p.d.f.s given in (2.31) or (5.3) (provided that
$\mathcal {S}\leqslant 0.2$) (full lines). The heavy positive tail associated with the present method is again evident, and is closer to the data than even the third-order distribution of Reference Longuet-HigginsLH63. In cases where the modified variant (5.3) has been utilized (again, figure 12b,c) oscillations in the negative tails are removed and the result matches the data reasonably. Based on these comparisons, it seems that the new p.d.f.s given in (2.31) or (5.3) (provided that ![]() $\mathcal {S}\leqslant 0.2$) are appropriate for practical use.
$\mathcal {S}\leqslant 0.2$) are appropriate for practical use.

Figure 12. Comparison of the p.d.f.s from (a) (2.31) and (b,c) (5.3) (full lines) with those from data generated using the fully nonlinear model of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021c) (circles, with error bars). The Gaussian distribution (dotted lines) and those from Reference Longuet-HigginsLH63 (second order, dashed lines; third order, dashed-dotted lines) are also provided as a reference. Cases utilize ![]() $N_D=2$ coupled with (a)
$N_D=2$ coupled with (a) ![]() $\varepsilon =0.1048$,
$\varepsilon =0.1048$, ![]() $k_ph=1.0$; (b)
$k_ph=1.0$; (b) ![]() $\varepsilon =0.1270$,
$\varepsilon =0.1270$, ![]() $k_ph=1.5$; and (c)
$k_ph=1.5$; and (c) ![]() $\varepsilon =0.1443$,
$\varepsilon =0.1443$, ![]() $k_ph=\infty$, with other statistical quantities given in table 2. The legend applies to all panels.
$k_ph=\infty$, with other statistical quantities given in table 2. The legend applies to all panels.
7. Example application of the new p.d.f. using sample data
It is clear that application of the new theoretical p.d.f. (2.31), or (if applicable) the variant with modified negative tail (5.3), requires that the skewness of the wave field be known. Likewise, knowing the skewness and kurtosis is a prerequisite for respectively applying the second- and third-order result of Reference Longuet-HigginsLH63 from (3.4). As these quantities must often be estimated from sample data (from e.g. numerical simulations or experimental or field measurements) in practice, an obvious question is: Does it actually make sense to estimate the required statistics from sample data and use them in combination with the desired p.d.f.? After all, it may be argued that one could simply estimate the p.d.f. directly from the sampled data.
To answer this question, suppose we have a record consisting of ![]() $n$ uncorrelated samples of the surface elevation. It is well known that the standard deviation of the skewness and the kurtosis (assuming Gaussian data and large sample size) are approximately
$n$ uncorrelated samples of the surface elevation. It is well known that the standard deviation of the skewness and the kurtosis (assuming Gaussian data and large sample size) are approximately ![]() $\sigma _\mathcal {S}=\sqrt {6/n}$ and
$\sigma _\mathcal {S}=\sqrt {6/n}$ and ![]() $\sigma _{\mathcal {K}}=\sqrt {24/n}$, respectively, dating back to Fisher (Reference Fisher1930). Due to their
$\sigma _{\mathcal {K}}=\sqrt {24/n}$, respectively, dating back to Fisher (Reference Fisher1930). Due to their ![]() $n^{-1/2}$ dependence, it appears that the uncertainties of the skewness and kurtosis decrease quite slowly, and that this might carry over to the distribution when used e.g. with the sample estimate of the skewness. However, the value of
$n^{-1/2}$ dependence, it appears that the uncertainties of the skewness and kurtosis decrease quite slowly, and that this might carry over to the distribution when used e.g. with the sample estimate of the skewness. However, the value of ![]() $n$ needed to bring
$n$ needed to bring ![]() $\sigma _{\mathcal {S}}$ and
$\sigma _{\mathcal {S}}$ and ![]() $\sigma _{\mathcal {K}}$ down to, say, a few per cent of
$\sigma _{\mathcal {K}}$ down to, say, a few per cent of ![]() $\mathcal {S}$ and
$\mathcal {S}$ and ![]() $\mathcal {K}$, respectively, is in fact not excessively large, and at this level of uncertainty the p.d.f.s are rather insensitive to associated uncertainties. Moreover, the uncertainty of the sampled distribution would typically be much larger, especially in the tails which will inevitably be poorly populated (if at all). (Note that there are errors in § 4.1 of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b), where coefficients 15 and 96, and similarly for subsequent calculations, should respectively be 6 and 24, in accordance with those above.)
$\mathcal {K}$, respectively, is in fact not excessively large, and at this level of uncertainty the p.d.f.s are rather insensitive to associated uncertainties. Moreover, the uncertainty of the sampled distribution would typically be much larger, especially in the tails which will inevitably be poorly populated (if at all). (Note that there are errors in § 4.1 of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021b), where coefficients 15 and 96, and similarly for subsequent calculations, should respectively be 6 and 24, in accordance with those above.)
To exemplify this, we will consider a single sample of the full data set utilized to create figure 9(b) (![]() $k_ph=1.2, \varepsilon =0.1524,\mathcal {S}=0.2688$), again generated utilizing the second-order irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012). The sample considered contains
$k_ph=1.2, \varepsilon =0.1524,\mathcal {S}=0.2688$), again generated utilizing the second-order irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012). The sample considered contains ![]() $n=$24,050 randomly sampled surface elevations, corresponding to 0.01 % of the full data set generated for this case. The sample has skewness
$n=$24,050 randomly sampled surface elevations, corresponding to 0.01 % of the full data set generated for this case. The sample has skewness ![]() $\mathcal {S}=0.2731$, with expected standard deviation
$\mathcal {S}=0.2731$, with expected standard deviation ![]() $\sigma _\mathcal {S}=0.0158$. The resulting p.d.f. created from the sampled data alone (using the same 0.2 bin size) is presented in figure 13 (circles, with error bars calculated as before). The theoretical p.d.f. from (2.31) utilizing the sample skewness is likewise presented as the full line, which is seen to closely resemble that from figure 9(b). Additionally, the theoretical p.d.f.s from (2.31), now utilizing
$\sigma _\mathcal {S}=0.0158$. The resulting p.d.f. created from the sampled data alone (using the same 0.2 bin size) is presented in figure 13 (circles, with error bars calculated as before). The theoretical p.d.f. from (2.31) utilizing the sample skewness is likewise presented as the full line, which is seen to closely resemble that from figure 9(b). Additionally, the theoretical p.d.f.s from (2.31), now utilizing ![]() $\mathcal {S}\pm \sigma _\mathcal {S}$, are shown as the dashed lines, such that the (very thin) region between them can be taken as an indication of the uncertainty in the theoretical p.d.f. As suggested above, this uncertainty is very small relative to that associated with the sample p.d.f. (as indicated by the error bars), especially e.g. in the (poorly populated) positive tail. Indeed, the sample p.d.f. could hardly be utilized at all in this example to reliably predict the distribution for say
$\mathcal {S}\pm \sigma _\mathcal {S}$, are shown as the dashed lines, such that the (very thin) region between them can be taken as an indication of the uncertainty in the theoretical p.d.f. As suggested above, this uncertainty is very small relative to that associated with the sample p.d.f. (as indicated by the error bars), especially e.g. in the (poorly populated) positive tail. Indeed, the sample p.d.f. could hardly be utilized at all in this example to reliably predict the distribution for say ![]() $\zeta >4$. Conversely, the uncertainty of the theoretical p.d.f. is small for the entire range shown, such that it may be reliably utilized to predict the theoretical probability of extreme surface elevations with say
$\zeta >4$. Conversely, the uncertainty of the theoretical p.d.f. is small for the entire range shown, such that it may be reliably utilized to predict the theoretical probability of extreme surface elevations with say ![]() $\zeta >6$. It is hoped that this example illustrates how the theoretical p.d.f. may be utilized in practice (including assessment of uncertainties), requiring only knowledge of the sample skewness and size.
$\zeta >6$. It is hoped that this example illustrates how the theoretical p.d.f. may be utilized in practice (including assessment of uncertainties), requiring only knowledge of the sample skewness and size.

Figure 13. Comparison of p.d.f.s based on sample data generated from the second-order irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012) (circles, with error bars), the new second-order p.d.f. (2.31) based on the sample skewness ![]() $\mathcal {S}=0.2731$ (full line) and the p.d.f. using
$\mathcal {S}=0.2731$ (full line) and the p.d.f. using ![]() $\mathcal {S}\pm \sigma _\mathcal {S}$ (dashed lines), where
$\mathcal {S}\pm \sigma _\mathcal {S}$ (dashed lines), where ![]() $\sigma _\mathcal {S}=0.0158$. The data utilized in this example (sample size
$\sigma _\mathcal {S}=0.0158$. The data utilized in this example (sample size ![]() $n=24\,050$) correspond to a random sample of 0.01 % of the full data set used to create figure 9(b).
$n=24\,050$) correspond to a random sample of 0.01 % of the full data set used to create figure 9(b).
8. Conclusions
In this work we have re-visited the derivation of the p.d.f. of the free surface elevation in an irregular sea, to second order in the wave steepness. To the order retained, we have derived exact results utilizing both moment and cumulant generating functions, and established their asymptotic equivalence in the limit of small skewness. The derivation of the p.d.f. stemming from the cumulant generating function has utilized a novel change in variables coupled with complex analysis, resulting in a new theoretical result, where the p.d.f. is expressed in terms of the Airy function, presented as (2.31) herein. Due to approximations made in his derivation, it is shown that the classical p.d.f. of Longuet-Higgins (Reference Longuet-Higgins1963) (referred to as Reference Longuet-HigginsLH63 herein), when truncated at second order, corresponds to that derived from the moment generating function, even though his derivation was based on the cumulant generating function. The new second-order p.d.f. predicts increased probability density of extreme positive surface elevations, typical of rogue waves, even relative to the third-order approximation of Reference Longuet-HigginsLH63. This heavy tail is inherent, and has been explained through comparison of the asymptotic forms of the p.d.f.s in the limit of large surface elevations. Similar to the p.d.f. of Reference Longuet-HigginsLH63, the new theoretical solution suffers from spurious oscillations (and negative probability densities) for moderate to extreme negative surface elevations. A semi-theoretical means for remedying this shortcoming has been developed, based on inspection of the envelope of the Airy functions having negative arguments. This modified variant of the p.d.f. is presented as (5.3) herein, and maintains reasonable statistical moments provided that the skewness is less than or equal to ![]() $0.2$. The new p.d.f.s have been compared against those from data sets involving storm conditions, generated from both second-order irregular wave theory as well as from simulations based on a fully nonlinear wave model. Good accuracy has been collectively demonstrated for the resulting p.d.f.s in both finite and infinite water depth, for varying degrees of directional spreading.
$0.2$. The new p.d.f.s have been compared against those from data sets involving storm conditions, generated from both second-order irregular wave theory as well as from simulations based on a fully nonlinear wave model. Good accuracy has been collectively demonstrated for the resulting p.d.f.s in both finite and infinite water depth, for varying degrees of directional spreading.
Supplementary material
Data utilized in the present study are freely available at https://doi.org/10.11583/DTU.21937232. The data set includes the surface elevation time series generated by the irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012) considered in § 6.1, as well as the surface elevation maps generated by the fully nonlinear PFL model of Klahn et al. (Reference Klahn, Madsen and Fuhrman2021c) considered in § 6.2. A Matlab function pdfAiry.m computing the new p.d.f. from (5.3) if ![]() $\mathcal {S}\leqslant 0.2$ and (2.31) otherwise is also provided. The PFL model is available as open source at https://github.com/MathiasKlahn/PFL-Wave-Model. Additionally, a Matlab implementation of the multi-directional irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012), complete to third order, is freely available at https://doi.org/10.11583/DTU.22060124.
$\mathcal {S}\leqslant 0.2$ and (2.31) otherwise is also provided. The PFL model is available as open source at https://github.com/MathiasKlahn/PFL-Wave-Model. Additionally, a Matlab implementation of the multi-directional irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012), complete to third order, is freely available at https://doi.org/10.11583/DTU.22060124.
Acknowledgements
The second author gratefully acknowledges help from two anonymous contributors at the Mathematics Stack Exchange, in working out a form of the integral in § 2.2 (thread: https://math.stackexchange.com/q/4403218). The first author likewise acknowledges enlightening discussions with Professor M. Benoit, which resulted in important revisions to § 5.1.
Funding
This research has been financially supported by the Independent Research Fund Denmark project STORM: STatistics and fOrces on stRuctures from extreMe water waves in finite depth (D.R.F., grant ID: 10.46540/2035-00064B). This support is greatly appreciated.
Declaration of interests
The authors report no conflicts of interest.
Appendix A. Corrigendum to the multi-directional irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012)
As the multi-directional irregular wave theory of Madsen & Fuhrman (Reference Madsen and Fuhrman2012) has (to second order) been utilized in the present work (§ 6.1), we take the opportunity to correct some unfortunate errors that appeared in the original paper, which have recently come to light. Below, equation numbers referred to and notation are as in Madsen & Fuhrman (Reference Madsen and Fuhrman2012). Known corrections follow.
The second part of (3.11) should read
Equation (3.83) should read
Finally, (3.84) should read
 \begin{equation} \mu_n^*= F_{13n}\cosh h\kappa_n + c_n^2\varXi_{nn} +\sum_{\substack{m=1 \\ m\!{\neq} n}}^N c_m^2\varXi_{nm}. \end{equation}
\begin{equation} \mu_n^*= F_{13n}\cosh h\kappa_n + c_n^2\varXi_{nn} +\sum_{\substack{m=1 \\ m\!{\neq} n}}^N c_m^2\varXi_{nm}. \end{equation}The errors above were first pointed out through personal communication initiated by Professor M. Benoit, which Professor P.A. Madsen and the present first author gratefully acknowledge.