Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-09T21:57:13.639Z Has data issue: false hasContentIssue false
  • English
  • Français

New bounds on the vertical heat transport for Bénard–Marangoni convection at infinite Prandtl number

Published online by Cambridge University Press:  27 December 2019

Giovanni Fantuzzi Open the ORCID record for Giovanni Fantuzzi [Opens in a new window] ,
Camilla Nobili  and
Andrew Wynn
Giovanni Fantuzzi*
Affiliation:
Department of Aeronautics, Imperial College London, LondonSW7 2AZ, UK
Camilla Nobili
Affiliation:
Department of Mathematics, University of Hamburg, 20146Hamburg, Germany
Andrew Wynn
Affiliation:
Department of Aeronautics, Imperial College London, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

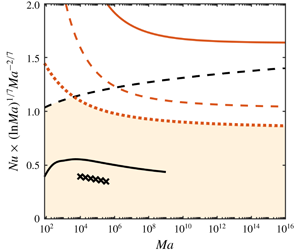
We prove a new rigorous upper bound on the vertical heat transport for Bénard–Marangoni  convection of a two- or three-dimensional fluid layer with infinite Prandtl number. Precisely, for Marangoni number $Ma\gg 1$ the Nusselt number $Nu$ is bounded asymptotically by $Nu\leqslant \text{const.}\times Ma^{2/7}(\ln Ma)^{-1/7}$. Key to our proof are a background temperature field with a hyperbolic profile near the fluid’s surface and new estimates for the coupling between temperature and vertical velocity.

JFM classification

Mathematical Foundations: Variational methods Convection: Marangoni convection
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , R4
Copyright
© The Author(s), 2019. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bénard, H. 1901 Les tourbillons cellulaires dans une nappe liquide – méthodes optiques d’observation et d’enregistrement. J. Phys. Theor. Appl. 10 (1), 254–266.CrossRefGoogle Scholar
Boeck, T. 2005 Bénard–Marangoni convection at large Marangoni numbers: results of numerical simulations. Adv. Space Res. 36 (1), 4–10.CrossRefGoogle Scholar
Boeck, T. & Thess, A. 1998 Turbulent Bénard–Marangoni convection: results of two-dimensional simulations. Phys. Rev. Lett. 80 (6), 1216–1219.CrossRefGoogle Scholar
Boeck, T. & Thess, A. 2001 Power-law scaling in Bénard–Marangoni convection at large Prandtl numbers. Phys. Rev. E 64 (2), 027303.Google ScholarPubMed
DebRoy, T. & David, S. A. 1995 Physical processes in fusion welding. Rev. Mod. Phys. 67 (1), 85–112.CrossRefGoogle Scholar
Doering, C. R. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69 (11), 1648–1651.CrossRefGoogle ScholarPubMed
Doering, C. R. & Gibbon, J. D. 1995 Applied Analysis of the Navier–Stokes Equations, Cambridge Texts in Applied Mathematics, vol. 12. Cambridge University Press.CrossRefGoogle Scholar
Doering, C. R., Otto, F. & Reznikoff, M. G. 2006 Bounds on vertical heat transport for infinite Prandtl number Rayleigh–Bénard convection. J. Fluid Mech. 560, 229–241.CrossRefGoogle Scholar
Fantuzzi, G., Pershin, A. & Wynn, A. 2018 Bounds on heat transfer for Bénard–Marangoni convection at infinite Prandtl number. J. Fluid Mech. 837, 562–596.CrossRefGoogle Scholar
Fantuzzi, G. & Wynn, A. 2017 Exact energy stability of Bénard–Marangoni convection at infinite Prandtl number. J. Fluid Mech. 822, R1.CrossRefGoogle Scholar
Hagstrom, G. I. & Doering, C. R. 2010 Bounds on heat transport in Bénard–Marangoni convection. Phys. Rev. E 81 (4), 047301.Google ScholarPubMed
Lappa, M. 2010 Thermal Convection: Patterns, Evolution and Stability. John Wiley & Sons Ltd.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225 (1161), 196–212.Google Scholar
Pearson, J. R. A. 1958 On convection cells induced by surface tension. J. Fluid Mech. 4 (5), 489–500.CrossRefGoogle Scholar
Pumir, A. & Blumenfeld, L. 1996 Heat transport in a liquid layer locally heated on its free surface. Phys. Rev. E 54 (5), R4528–R4531.Google Scholar
Whitehead, J. P. & Doering, C. R. 2011 Internal heating driven convection at infinite Prandtl number. J. Math. Phys. 52 (9), 093101.CrossRefGoogle Scholar
Whitehead, J. P. & Wittenberg, R. W. 2014 A rigorous bound on the vertical transport of heat in Rayleigh–Bénard convection at infinite Prandtl number with mixed thermal boundary conditions. J. Math. Phys. 55 (9), 093104.CrossRefGoogle Scholar