Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-17T11:24:54.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-wall statistics of a turbulent pipe flow at shear Reynolds numbers up to 40 000

Published online by Cambridge University Press:  15 August 2017

Christian E. Willert Open the ORCID record for Christian E. Willert [Opens in a new window] ,
Julio Soria Open the ORCID record for Julio Soria [Opens in a new window] ,
Michel Stanislas ,
Joachim Klinner ,
Omid Amili ,
Michael Eisfelder ,
Christophe Cuvier ,
Gabriele Bellani ,
Tommaso Fiorini  and
Alessandro Talamelli
Christian E. Willert*
Affiliation:
DLR Institute of Propulsion Technology, 51170 Köln, Germany
Julio Soria
Affiliation:
LTRAC, Department of Mechanical and Aerospace Engineering, Monash University, Clayton Campus, Melbourne, VIC 3800, Australia Department of Aeronautical Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia
Michel Stanislas
Affiliation:
LML, Ecole Centrale de Lille, France
Joachim Klinner
Affiliation:
DLR Institute of Propulsion Technology, 51170 Köln, Germany
Omid Amili
Affiliation:
LTRAC, Department of Mechanical and Aerospace Engineering, Monash University, Clayton Campus, Melbourne, VIC 3800, Australia Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN, USA
Michael Eisfelder
Affiliation:
LTRAC, Department of Mechanical and Aerospace Engineering, Monash University, Clayton Campus, Melbourne, VIC 3800, Australia
Christophe Cuvier
Affiliation:
LML, Ecole Centrale de Lille, France
Gabriele Bellani
Affiliation:
CIRI Aeronautics, University of Bologna, Italy
Tommaso Fiorini
Affiliation:
CIRI Aeronautics, University of Bologna, Italy
Alessandro Talamelli
Affiliation:
CIRI Aeronautics, University of Bologna, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

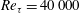This paper reports on near-wall two-component–two-dimensional (2C–2D) particle image velocimetry (PIV) measurements of a turbulent pipe flow at shear Reynolds numbers up to $Re_{\unicode[STIX]{x1D70F}}=40\,000$ acquired in the CICLoPE facility of the University of Bologna. The 111.5 m long pipe of 900 mm diameter offers a well-established turbulent flow with viscous length scales ranging from 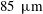$85~\unicode[STIX]{x03BC}\text{m}$ at 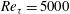$Re_{\unicode[STIX]{x1D70F}}=5000$ down to 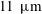$11~\unicode[STIX]{x03BC}\text{m}$ at 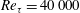$Re_{\unicode[STIX]{x1D70F}}=40\,000$. These length scales can be resolved with a high-speed PIV camera at image magnification near unity. Statistically converged velocity profiles were determined using multiple sequences of up to 70 000 PIV recordings acquired at sampling rates of 100 Hz up to 10 kHz. Analysis of the velocity statistics shows a well-resolved inner peak of the streamwise velocity fluctuations that grows with increasing Reynolds number and an outer peak that develops and moves away from the inner peak with increasing Reynolds number.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent boundary layers
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , R5
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahn, J., Lee, J. H., Lee, J., Kang, J.-H. & Sung, H. J. 2015 Direct numerical simulation of a 30R long turbulent pipe flow at Re 𝜏 = 3008. Phys. Fluids 27 (6), 065110.Google Scholar
Benedict, L. H. & Gould, R. D. 1996 Towards better uncertainty estimates for turbulence statistics. Exp. Fluids 22 (2), 129–136.Google Scholar
Carlier, J. & Stanislas, M. 2005 Experimental study of eddy structures in a turbulent boundary layer using particle image velocimetry. J. Fluid Mech. 535, 143–188.CrossRefGoogle Scholar
Cuvier, C., Srinath, S., Stanislas, M., Foucaut, J. M., Laval, J. P., Kähler, C. J., Hain, R., Scharnowski, S., Schröder, A., Geisler, R. et al. 2017 Extensive characterization of a high Reynolds number decelerating boundary layer using advanced optical metrology. J. Turbul. doi:10.1080/14685248.2017.1342827.Google Scholar
Fiorini, T.2017 Turbulent pipe flow – high resolution measurements in CICLoPE. PhD thesis, University of Bologna.Google Scholar
Foucaut, J. M., Carlier, J. & Stanislas, M. 2004 PIV optimization for the study of turbulent flow using spectral analysis. Meas. Sci. Technol. 15 (6), 1046–1058.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2012 Turbulent pipe flow at extreme Reynolds numbers. Phys. Rev. Lett. 108, 094501.Google Scholar
Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Logarithmic scaling of turbulence in smooth- and rough-wall pipe flow. J. Fluid Mech. 728, 376–395.CrossRefGoogle Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 635, 103–136.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up toRe 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014 Effect of the computational domain on direct simulations of turbulent channels up to Re𝜏 = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Örlü, R., Fiorini, T., Segalini, A., Bellani, G., Talamelli, A. & Alfredsson, P. H. 2017 Reynolds stress scaling in pipe flow turbulence – first results from CICLoPE. Phil. Trans. R. Soc. Lond. A 375, 20160187.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Pullin, D. I., Inoue, M. & Saito, N. 2013 On the asymptotic state of high Reynolds number, smooth-wall turbulent flows. Phys. Fluids 25 (1), 015116.CrossRefGoogle Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25 (2), 025104.Google Scholar
Sillero, J. A., Jimenez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to 𝛿+ ≈ 2000. Phys. Fluids 26 (10).Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.Google Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12, 221–233.Google Scholar
Soria, J., Willert, C., Amili, O., Klinner, J., Atkinson, C., Stanislas, M., Schröder, A., Geisler, R., Agocs, J., Röse, A. et al. 2016 Spatially and temporally resolved 2C–2D PIV in the inner layer of a high Reynolds number adverse pressure gradient turbulent boundary layer. In 18th International Symposium on the Application of Laser and Imaging Techniques to Fluid Mechanics, Lisbon (Portugal), July 4–7, 2016. Center for Innovation Technology and Policy Research, Instituto Superior Técnico Lisboa. ISBN 978-989-98777-8-8 from https://www.lisbonsimposia.org/blank-cjg9.Google Scholar
Talamelli, A., Persiani, F., Fransson, J. H. M., Alfredsson, P. H., Johansson, A. V., Nagib, H. M., Redi, J.-D., Sreenivasan, K. R. & Monkewitz, P. A. 2009 CICLoPE – a response to the need for high Reynolds number experiments. Fluid Dyn. Res. 41 (2), 021407.Google Scholar
Vallikivi, M., Ganapathisubramani, B. & Smits, A. J. 2015 Spectral scaling in boundary layers and pipes at very high Reynolds numbers. J. Fluid Mech. 771, 303–326.Google Scholar
Willert, C. E. 2015 High-speed particle image velocimetry for the efficient measurement of turbulence statistics. Exp. Fluids 56, 17.Google Scholar
Willert, C. E. & Gharib, M. 1991 Digital particle image velocimetry. Exp. Fluids 10, 181–193.Google Scholar