2. Multi-time-scale wall model: from full equilibrium to non-equilibrium

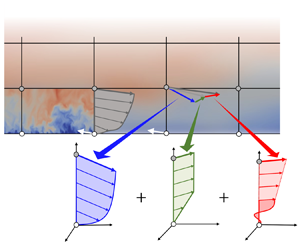
We begin with a summary schematic containing all the constitutive parts of the MTS wall model. Figure 1 includes the full spectrum of length and time scales captured in this approach. The wall-modelling region is confined between the wall and the wall-modelling height $y=\varDelta$, whereas the ‘LES region’ exists above, beyond $y=\varDelta$. The total wall stress in the MTS wall model is evaluated as the superposition between the quasi-equilibrium, lamNEQ and turbNEQ components:

(2.1)\begin{equation} \boldsymbol{\tau}_w(x,z,t) = \bar{\boldsymbol \tau}_w(x,z,t) + \boldsymbol{\tau}_w''(x,z,t) + \boldsymbol{\tau}_w'(x,z,t).\end{equation}

The quasi-equilibrium component $\bar {\boldsymbol \tau }_w$ is modelled via the LaRTE wall model first introduced in Fowler et al. (Reference Fowler, Zaki and Meneveau2022) and reviewed in § 2.1. The LaRTE model is named according to its governing equation for the friction-velocity vector $\boldsymbol {u}_\tau$, which relaxes to its equilibrium value in a Lagrangian manner at a rate $T_s$ called the relaxation time scale. Therefore, the LaRTE model captures the quasi-equilibrium behaviour of the wall stress, which occurs at time scales longer than the relaxation time scale. In figure 1, the LaRTE region is shown in blue, with relaxation represented by the dark blue arrow pointing to the dark grey equilibrium closure region.

Figure 1. Multi-time-scale wall model length and time scales.

The LaRTE model is further supplemented by lamNEQ and turbNEQ models to capture wall-stress dynamics faster than $T_s$. The lamNEQ component $\boldsymbol {\tau }_w''$ covers fast dynamics resulting from the pressure gradient forcing at time scales faster than a viscous time scale, $t_\nu \sim \nu /u_\tau ^2$ (where $\nu$ is the kinematic fluid viscosity, and $u_\tau$ is the friction velocity). This laminar ‘Stokes-like’ behaviour is assumed to be confined to the laminar viscous sublayer. For intermediate time scales, i.e. for time scales between $t_\nu$ and $T_s$, turbulent eddies that would occur between the wall and $y=\varDelta$ but cannot be reproduced by LES must also be modelled. In this paper (§ 2.3), we develop a turbNEQ wall model that completes the spectrum of time scales covered by the MTS wall model.

Generally, the model terms are distinguished by the following notation and colours (abbreviated model name, symbol, colour in parentheses): quasi-equilibrium is marked by overline (LaRTE, $\bar {\phi }$, blue), laminar non-equilibrium by double prime (lamNEQ, $\phi ''$, red), turbulent non-equilibrium by single prime (turbNEQ, $\phi '$, green), and full equilibrium by superscript ‘eq’ ($\phi ^{eq}$, grey), where $\phi$ represents any relevant model variable. Averaging over the homogeneous directions (and ensemble averaging, if applicable) is denoted with angled brackets, with the subscript identifying any additional variables over which averaging is done, i.e. $\langle \cdot \rangle$ indicates averaging over $x$ and $z$, and $\langle \cdot \rangle _t$ indicates averaging over $x$, $z$ and $t$.

2.1. Quasi-equilibrium (LaRTE)

First, we summarize the primary governing equations for the LaRTE portion of the MTS wall model. Derivations and additional details are discussed in Fowler et al. (Reference Fowler, Zaki and Meneveau2022). The goal of the LaRTE portion is to capture quasi-equilibrium dynamics of the wall stress. This is achieved by assuming an equilibrium mean-velocity profile in the near-wall region, whose dimensional parameter (friction velocity) is allowed to evolve slowly in both space and time. Generally, a slow, quasi-equilibrium quantity with LES horizontal resolution is indicated with an overline. For all present applications, we assume that the horizontal quasi-equilibrium velocity $\bar {\boldsymbol u}_s = \bar {u} \hat {\boldsymbol \imath } + \bar {w} \hat {\boldsymbol k}$ satisfies the law of the wall

(2.2)\begin{equation} \bar{\boldsymbol u}_s(x,y,z,t) = {\boldsymbol u}_{\tau}(x,z,t)\,f(y^+),\end{equation}

where ${\boldsymbol u}_\tau (x,z,t)$ is the friction-velocity vector and is a slowly varying function of the horizontal coordinates $(x,z)$ and time $t$. A schematic of this velocity profile is shown in figure 2(a). The quasi-equilibrium wall-stress vector can be found from the friction-velocity vector using

(2.3)\begin{equation} \bar{\boldsymbol \tau}_w = u_{\tau} {\boldsymbol u}_{\tau}. \end{equation}

Figure 2. A schematic of the velocity profiles for the (a) LaRTE, (b) laminar non-equilibrium, and (c) turbulent non-equilibrium components. Additional visualizations (including an interactive animation) of the various terms comprising the MTS wall model are provided in Appendix A, in figure 27.

LaRTE is based on an evolution equation for the friction-velocity vector $\boldsymbol {u}_\tau (x,z,t)$, from which the wall stress can then be computed. The evolution of $\boldsymbol {u}_\tau (x,z,t)$ is based on an unsteady Reynolds-averaged Navier–Stokes momentum equation for $\bar {\boldsymbol u}_s(x,y,z,t)$, the wall-parallel Reynolds averaged velocity as a function of vertical position $y$. The momentum balance governing this velocity is

(2.4)\begin{align} &\frac{\partial \bar{\boldsymbol u}_s}{\partial t} + \boldsymbol{\nabla}_h \boldsymbol{\cdot} ( \bar{\boldsymbol u}_s \bar{\boldsymbol u}_s ) + \partial_y ( \bar{v} \bar{\boldsymbol u}_s ) ={-} \frac{1}{\rho}\,\boldsymbol{\nabla}_h\bar{p} + \frac{\partial}{\partial y} \left[ (\nu+\nu_T)\, \frac{\partial \bar{\boldsymbol u}_s}{\partial y} \right] \nonumber\\ &\quad + \boldsymbol{\nabla}_h \boldsymbol{\cdot} [(\nu+\nu_T) ( \boldsymbol{\nabla}_h \bar{\boldsymbol u}_s+\boldsymbol{\nabla}_h \bar{\boldsymbol u}_s^{\rm T} )], \end{align}

where $\boldsymbol {\nabla }_h=\partial _x \hat {\boldsymbol \imath } +\partial _z \hat {\boldsymbol k}$ represents the horizontal gradients on the $x$–$z$ wall plane, and the total (viscous plus eddy) diffusion cross-terms involving the (small) vertical velocity $\bar {v}$ have been neglected. This partial differential equation (PDE) is then integrated vertically from the wall to the wall-model height $y=\varDelta$, and the assumed velocity profile (2.2) is substituted to get all terms as a function of ${\boldsymbol {u}}_\tau$. After simplifying the PDE, i.e. neglecting horizontal diffusion terms as well as a term representing the horizontal divergence of the friction-velocity direction vector (see Appendix B, which provides an alternative derivation of the LaRTE equation from that presented in Fowler et al. Reference Fowler, Zaki and Meneveau2022), the following evolution equation for the friction-velocity vector is obtained:

(2.5)\begin{equation} \frac{\partial {\boldsymbol{u}}_\tau}{\partial t} + {\boldsymbol V}_\tau \boldsymbol{\cdot} \boldsymbol{\nabla}_h {\boldsymbol{u}}_\tau = \frac{1}{T_s} \left[ \frac{1}{u_\tau}\left(-\frac{\varDelta}{\rho}\, \boldsymbol{\nabla}_h \bar{p} + \bar{\boldsymbol{\tau}}_\varDelta \right) - {\boldsymbol u}_\tau\right] + u_\tau\, \frac{\delta^*_\varDelta}{\varDelta}\, \frac{\partial {\boldsymbol s}}{\partial t},\end{equation}

where

(2.6)\begin{equation} T_s \equiv f(\varDelta^+)\,\frac{\varDelta }{u_\tau} \end{equation}

appears formally as a relaxation time scale, $\boldsymbol {s} \equiv \boldsymbol {u}_\tau /u_\tau$ is the unit friction-velocity vector,

(2.7)\begin{equation} \bar{\boldsymbol \tau}_\varDelta \equiv \left. (\nu+\nu_T)\,\frac{\partial \bar{\boldsymbol u}_s}{\partial y} \right|_{y=\varDelta}, \end{equation}

is the total shear stress (including viscous and turbulent stresses) at the wall-model height $y=\varDelta$, ${\boldsymbol V}_\tau \equiv (1-{\delta ^*_\varDelta }/{\varDelta } - {\theta _\varDelta }/{\varDelta })\, f(\varDelta ^+)\,{\boldsymbol u}_\tau$ is the advection velocity for the friction-velocity vector, and $\delta ^*_\varDelta \equiv \int _0^\varDelta (1-{\bar {u}_s(y)}/{\bar {u}_s(\varDelta )} ) \, {{\rm d} y}$ and $\theta _\varDelta \equiv \int _0^\varDelta ({\bar {u}_s(y)}/{\bar {u}_s(\varDelta )}) (1-{\bar {u}_s(y)}/{\bar {u}_s(\varDelta )} ) \, {{\rm d} y}$ are the cell displacement and momentum thicknesses, respectively. In this equation, the friction velocity relaxes in a Lagrangian fashion (with velocity ${\boldsymbol V}_\tau$), to its equilibrium value ((2.13), introduced later in this subsection). Hence the model was termed the Lagrangian relaxation towards equilibrium (LaRTE) wall model.

The LaRTE evolution equation is discretized in time using a forward Euler method for explicit evaluation of $\boldsymbol {u}_\tau$. To evaluate spatial gradients that arise from the advection term in the Lagrangian time derivative, we use a semi-Lagrangian scheme (Staniforth & Côté Reference Staniforth and Côté1991) where the right-hand side of (2.5) is evaluated at the upstream location using bilinear spatial interpolation. The additional numerical diffusion caused by the discretization scheme furthermore reduces the need to evaluate the horizontal diffusion term, thus we opt to neglect it. Specifics for evaluating (2.5) may be found in Fowler et al. (Reference Fowler, Zaki and Meneveau2022).

The term towards which the friction velocity relaxes includes contributions from both the pressure gradient and the total stress at the wall-model height. The LES information (velocity and pressure gradient) contains the full spectrum of time scales resolved by the LES. Therefore, we must remove explicitly the effects of the fast laminar Stokes layer behaviour from the LES inputs, otherwise the friction velocity will relax to an incorrect value. For the quasi-equilibrium pressure gradient, this is done through a one-sided exponential filter that is evaluated as

(2.8)\begin{equation} \boldsymbol{\nabla}_h\overline{p}^n = \frac{\delta t^n}{t_\nu}\,\boldsymbol{\nabla}_h p_{LES}^n + \left( 1 - \frac{\delta t^n}{t_\nu}\right) \boldsymbol{\nabla}_h\overline{p}^{n-1},\end{equation}

where $n$ is the time step index, $\delta t$ is the time step size, $\boldsymbol {\nabla }_h p_{LES}$ is the LES pressure gradient at the location $(x,\varDelta,z)$, and $t_\nu$ is a viscous diffusion time scale associated with the laminar Stokes layer. The laminar diffusion time scale $t_\nu \sim l^2_s/\nu$ is defined based on the assumption that the laminar Stokes layer is confined to the region from the wall to a height $l_s$ in which viscous effects dominate over inertial ones. The thickness of the viscous sublayer is fixed in inner units, therefore we express $t_\nu$ in terms of $l_s^+= l_s u_\tau /\nu$ according to

(2.9)\begin{equation} t_\nu \equiv (l_s^+)^2 \nu/u_\tau^2, \quad {\rm where}\ l_s^+{=} 12. \end{equation}

This viscous time scale represents the time it takes for a Stokes layer to propagate from the wall to the edge of the viscous sublayer. Throughout this paper, $l_s^+ = 12$ is used. This value marks the intercept between the log law and linear viscous sublayer velocity profiles with the von Kármán constant $\kappa =0.4$ and log-law intercept $B=5.8$. This value also agrees with the viscous sublayer thickness estimated by Nickels (Reference Nickels2004) (called $y_c^+$ in that work).

The total stress at $y=\varDelta$, i.e. $\bar {\boldsymbol \tau }_\varDelta$, is the primary term to be closed in (2.5). The LaRTE wall model uses an equilibrium closure for evaluating the total stress but with a ‘velocity correction’ to the LES velocity that removes the contribution of the laminar Stokes layer to the LES velocity, similar to what was done for the quasi-equilibrium pressure gradient. The total stress closure is based on the full equilibrium momentum balance, where the unsteady and advection terms are set to zero. The smooth-walled, full equilibrium solution is found by solving the ordinary differential equation

(2.10)\begin{equation} 0 ={-}\frac{1}{\rho}\,\boldsymbol{\nabla}_h \bar{p} + \frac{{\rm d}}{{\rm d} y}\left( (\nu+\nu_T)\,\frac{{\rm d} \bar{\boldsymbol u}^{eq} }{{\rm d} y}\right),\end{equation}

with boundary conditions

(2.11a,b)\begin{equation} \bar{\boldsymbol u}^{eq} (0) = \boldsymbol{0}, \quad \bar{\boldsymbol u}^{eq}(\varDelta) = \bar{\boldsymbol u}_\varDelta, \end{equation}

where $\varDelta$ is the wall-model height, and $\bar {\boldsymbol u}_\varDelta$ is the velocity input to the model. This velocity is related (but not exactly equal) to the LES velocity at $y=\varDelta$, $\boldsymbol {U}_{LES}$ (as discussed further in this section). The pressure gradient $\boldsymbol {\nabla }_h \bar {p}$ is determined from the LES pressure gradient by low-pass filtering it at a viscous time scale, as introduced in (2.8). Finally, the eddy viscosity is assumed to be unaffected by the pressure gradient and is evaluated as $\nu _T(y)=[D(y)\,\kappa y]^2\|{\rm d} \bar {\boldsymbol u}^{eq} /{{\rm d} y}\|$, where $D(y)$ is the van Driest damping function (van Driest Reference van Driest1956).

Integrating (2.10) between $y=0$ and $y=\varDelta$, one obtains

(2.12)\begin{equation} 0 ={-}\frac{\varDelta}{\rho}\,\boldsymbol{\nabla}_h \bar{p} + \bar{\boldsymbol{\tau}}_\varDelta - \bar{\boldsymbol \tau}_w^{eq}, \quad {\rm where} \ \bar{\boldsymbol \tau}_w^{eq} \equiv \left. \nu\,\frac{{\rm d} \bar{\boldsymbol u}^{eq}}{{\rm d} y} \right|_0. \end{equation}

The equilibrium wall stress $\bar {\boldsymbol \tau }_w^{eq}$ is the viscous stress at the wall involving the solution $\bar {\boldsymbol u}^{eq}(y)$ to (2.10). The obtained equilibrium wall stress, appropriately non-dimensionalized, was fitted for general use in Meneveau (Reference Meneveau2020), expressing the result in terms of a wall-model friction factor $c_{f}^{wm,eq}(Re_\varDelta,\psi _p)\equiv 2 \bar {\tau }_w^{eq}/\bar {u}_\varDelta ^2$, or equivalently, a wall friction Reynolds number $Re_{\tau \varDelta }^{pres}(Re_\varDelta,\psi _p)\equiv \varDelta (\bar {\tau }_w^{eq})^{1/2}/\nu$, where the inputs to the fit are $Re_\varDelta \equiv \bar {u}_\varDelta \varDelta /\nu$ and $\psi _p \equiv ({1}/{\rho })(\boldsymbol {\nabla }_h \bar {p} \boldsymbol {\cdot } \hat {\boldsymbol e}_u) {\varDelta ^3}/{\nu ^2}$, with $\hat {\boldsymbol e}_u \equiv \bar {\boldsymbol u}_\varDelta /\bar {u}_\varDelta$ the velocity input unit vector. Both are related via $c_{f}^{wm,eq}=2 [ Re_{\tau \varDelta }^{pres} / Re_{\varDelta } ]^2$ (see Meneveau (Reference Meneveau2020) and Fowler et al. (Reference Fowler, Zaki and Meneveau2022) for more details). Full equilibrium implies that we may use the equilibrium wall model of $\bar {\boldsymbol \tau }_w^{eq}$ as a model for the total forcing at $y=\varDelta$, namely we replace

(2.13)\begin{equation} -\frac{\varDelta}{\rho}\,\boldsymbol{\nabla}_h \bar{p} + \bar{\boldsymbol{\tau}}_\varDelta = \bar{\boldsymbol \tau}_w^{eq} = \frac{1}{2}\, c_{f}^{wm,eq}(Re_\varDelta,\psi_p)\, \bar{u}_\varDelta^2 \hat{\boldsymbol e}_u\end{equation}

in (2.5).

During LES of flows under strong non-equilibrium conditions, we have found that simply using the LES velocity $\boldsymbol {U}_{LES}$ as the input to the stress closure for $\bar {\boldsymbol \tau }_w^{eq}$ (i.e. using $Re_\varDelta = U_{LES} \varDelta /\nu$) yields incorrect results during periods of high non-equilibrium forcing. For example, if the flow is accelerated in the streamwise direction by a sudden increase in the pressure gradient, then a shear layer grows near the wall and the velocity outside the shear layer increases. If we were to use the LES velocity as the input, then (2.13) incorrectly attributes the increase in velocity to an increase in the turbulence and the wall stress. Ample evidence from the literature (He & Jackson Reference He and Jackson2000; Greenblatt & Moss Reference Greenblatt and Moss2004; He et al. Reference He, Ariyaratne and Vardy2008; He & Seddighi Reference He and Seddighi2013; Vardy et al. Reference Vardy, Brown, He, Ariyaratne and Gorji2015; Sundstrom & Cervantes Reference Sundstrom and Cervantes2018a) shows that the stress outside of this shear layer remains unchanged for some time after application of the sudden change in the pressure gradient, consistent with the concept of ‘frozen turbulence’. To mimic this effect while also keeping the simplicity of the equilibrium wall model, we correct the LES velocity by subtracting from it the anticipated increase in velocity due to rapid changes in pressure gradient. This velocity correction is denoted as $\boldsymbol {u}_\varDelta ''$ and is modelled as the solution to the model equation

(2.14)\begin{equation} \frac{\partial \boldsymbol{u}_{\varDelta}''}{\partial t} ={-}\frac{1}{\rho}\,\boldsymbol{\nabla}_h p'' -\frac{\boldsymbol{u}_{\varDelta}''}{T_\varDelta},\end{equation}

where $T_\varDelta = t_\nu + \varDelta /\kappa u_\tau$ represents the time scale associated with the destruction of the laminar Stokes layer as it diffuses away from the wall. In the absence of mean shear, the fluid acceleration is equal to the pressure gradient. However, because the underlying flow has shear, the laminar Stokes layer above $l_s$ weakens and becomes turbulent as it diffuses away from the wall. The characteristic time for this diffusive process to take place, $T_\varDelta$, is modelled as the time it takes for the laminar Stokes layer to diffuse to the edge of the viscous sublayer, $t_\nu$, plus the eddy turnover time at the wall-model height, $\varDelta ^2/\nu _T(\varDelta ) = \varDelta /\kappa u_\tau$. In figures 1 and 2, the dark red region corresponds to the laminar Stokes layer near the wall, which diffuses to the edge of the viscous sublayer, $l_s$, by time $t_\nu$. The Stokes layer's growth is then interrupted by the turbulent flow, which further diffuses it over an eddy turnover time. This is represented by the light red region in figures 1 and 2. Here, $\boldsymbol {\nabla }_h p'' \equiv \boldsymbol {\nabla }_h p_{LES} - \boldsymbol {\nabla }_h \bar {p}$ is the high-pass filtered non-equilibrium pressure gradient containing the high-frequency content of the LES pressure gradient affecting mostly the laminar sublayer dynamics. Equation (2.14) effectively models the changes in the LES velocity due to fast changes in the pressure gradient. Note the similarities between (2.14) and (2.16), soon to be introduced. Equation (2.14) is essentially a model for (2.16) evaluated at the wall-model height $\varDelta$ where the viscous term is replaced by a modelled destruction term.

The velocity input used in (2.13) is then given by

(2.15)\begin{equation} \bar{\boldsymbol u}_\varDelta = \boldsymbol{U}_{LES} - \boldsymbol{u}_\varDelta''.\end{equation}

The velocity correction $\boldsymbol {u}_\varDelta ''$ is shown schematically with the thick red vector in figure 2, and the resulting corrected velocity input $\bar {\boldsymbol u}_\varDelta$ is shown by the light grey vector. During non-equilibrium events, $\boldsymbol {u}_\varDelta ''$ cancels the changes in the LES velocity, which ultimately leads to a delayed response by $\bar {\boldsymbol \tau }_\varDelta$. In previous applications of the LaRTE wall model (Fowler et al. Reference Fowler, Zaki and Meneveau2022), $\boldsymbol {U}_{LES}$ was filtered using a $2\varDelta$ spatial filter to remove LES velocity fluctuations that ultimately lead to an overpredicted wall stress (Bou-Zeid, Meneveau & Parlange Reference Bou-Zeid, Meneveau and Parlange2005). However, we have found that the velocity correction eliminates the need to filter the LES velocity since it inherently removes the high-frequency content in $\boldsymbol {U}_{LES}$. Therefore, in the present test cases using the LaRTE wall model, the LES velocity remains spatially unfiltered.

2.2. Laminar non-equilibrium

The lamNEQ wall model developed in Fowler et al. (Reference Fowler, Zaki and Meneveau2022) is based on the concept of frozen turbulence where the Reynolds stresses remain unaffected during a short period after a fast change in the pressure gradient forcing. Since the Reynolds stresses may be neglected, the resulting governing equation for this process is laminar. The lamNEQ velocity $\boldsymbol {u}''$ is then modelled by solving

(2.16)\begin{equation} \frac{\partial \boldsymbol{u}''}{\partial t} ={-} \frac{1}{\rho}\,\boldsymbol{\nabla}_h p'' + \nu\, \frac{\partial^2 \boldsymbol{u}''}{\partial y^2},\end{equation}

where

(2.17)\begin{equation} \boldsymbol{\nabla}_h p'' = \boldsymbol{\nabla}_h p_{LES} - \boldsymbol{\nabla}_h \bar{p}\end{equation}

may be interpreted as the high-frequency pressure gradient fluctuations around the LaRTE quasi-equilibrium pressure gradient (see (2.8) for the evaluation of $\boldsymbol {\nabla }_h \bar {p}$). The resulting flow is confined to a thin region near the wall where the flow is quasi-parallel and advection terms may be neglected, therefore ${\boldsymbol \nabla }_h p''$ is the sole driving force for accelerating the flow. The solution to (2.16) is represented in figure 2 by the dark red Stokes layer profile near the wall.

Analytical solutions to (2.16) can be obtained, from which we find the lamNEQ wall stress to be

(2.18)\begin{equation} \boldsymbol{\tau}_w''(t) = \sqrt{\nu/{\rm \pi}} \int_{t_0}^t - \frac{1}{\rho}\,\boldsymbol{\nabla}_h p''(t')\, (t - t')^{{-}1/2} \, {\rm d} t'. \end{equation}

Efficient evaluation of (2.18) is challenging due to the non-local nature of the convolution integral. For practical implementation, we use the ‘sum-of-exponentials’ method developed by Jiang et al. (Reference Jiang, Zhang, Zhang and Zhang2017). In this method, the kernel is approximated as a sum of exponential terms

(2.19)\begin{equation} (t_n - t')^{{-}1/2} \approx \sum_{m=1}^{N_{exp}} \omega_m \, {\rm e}^{{-}s_m (t_n - t')}, \end{equation}

where the constants $\omega _m$ and $s_m$ are determined a priori. The number of exponential terms, $N_{exp}$, is fixed in time, therefore leading to reduced storage and computation requirements. Upon substituting (2.19) into (2.18), one can show that the integral can be evaluated recursively. Exponential time filtering is known to be advantageous because the recursive structure does not require storing the entire time evolution, and the current time-filtered variable depends only on the filtered value at the last time step and the current increment (Meneveau, Lund & Cabot Reference Meneveau, Lund and Cabot1996). The advantage of this method is that it requires $O(N_{exp})$ storage and $O(N_T N_{exp})$ computational work, whereas a direct method requires storing the entire time evolution, i.e. $O(N_T)$ storage and $O(N_T^2)$ work, which becomes unwieldy for long simulations. The accuracy of this algorithm was tested and verified in Fowler et al. (Reference Fowler, Zaki and Meneveau2022).

2.3. Turbulent non-equilibrium

The wall-model physics described so far captures the slow, quasi-equilibrium behaviour and the fast, lamNEQ behaviour caused by fast changes in the pressure gradient. The velocities associated with each of these models are governed by (2.2) and (2.14) for the LaRTE and lamNEQ models, respectively. We now introduce a simple model that accounts for the velocity difference between the LES velocity and the LaRTE and lamNEQ models. This velocity deficit is expressed as

(2.20)\begin{equation} \boldsymbol{u}_\varDelta' = \bar{\boldsymbol u}_\varDelta - \boldsymbol{u}_\tau\,f(\varDelta^+) = \boldsymbol{U}_{LES} - \boldsymbol{u}_{\varDelta}'' - \boldsymbol{u}_\tau\,f(\varDelta^+),\end{equation}

and is represented in figure 2 by a thick green vector. Turbulent non-equilibrium is assumed to occur when turbulence affects the velocity profile at a rate faster than the relaxation time scale, thus the LaRTE model is unable to account for this effect.

Since $\boldsymbol {U}_{LES}$ is known from the simulation, and the laminar velocity $\boldsymbol {u}_\varDelta ''$ and LaRTE velocity contribution are known from their respective models, during LES, the remainder represents the turbulence that is left out and not yet included in the wall model. While this velocity can be computed during LES based on (2.20), what remains is to determine the contribution to the wall stress from turbulent flow structures that are associated with the velocity fluctuation $\boldsymbol {u}_\varDelta '$. For this purpose, we invoke the attached eddy hypothesis of Townsend (Reference Townsend1976), which has been refined further in various more recent works (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011; Marusic & Monty Reference Marusic and Monty2019). Based on the attached eddy hypothesis, $\boldsymbol {u}_{\varDelta }'$ may be viewed as a turbulent velocity fluctuation caused by the large, wall-attached eddies with height of the order of $\varDelta$, as portrayed in figure 3. We are interested only in the wall stress filtered to the LES resolution, i.e. the local average of effects of eddies over the LES resolution. It is this local average that is associated with the velocity fluctuation $\boldsymbol {u}_\varDelta '$. The contribution of eddies smaller than $\varDelta x \times \varDelta \times \varDelta z$ is neglected. In the absence of additional information or any further assumptions, we model the resulting flow structures as consisting of streamwise elongated high- and low-speed regions in which the velocity profile is approximated as mostly plug flow. When approaching the wall, one assumes that there is a linear shear layer connecting the profile to the no-slip boundary condition on the smooth wall. We assume that this layer has the thickness of the viscous sublayer (the same as that assumed for the Stokes layer, $l_s$). The turbNEQ velocity is then

(2.21) \begin{equation} \left. \begin{array}{ll@{}} \boldsymbol{u}' = \boldsymbol{u}_\varDelta'\, \dfrac{y}{l_s} & \textrm{for} \ 0 \leq y \leq l_s, \\ \boldsymbol{u}' = \boldsymbol{u}_\varDelta' & \textrm{for} \ y \geq l_s, \end{array}\right\} \end{equation}

where $l_s = l_s^+ \nu /u_\tau$ with $l_s^+=12$, and the friction velocity $u_\tau$ comes from the LaRTE model. The wall stress is then computed as

(2.22)\begin{equation} \boldsymbol{\tau}_w' \equiv \left. \nu\, \frac{\partial \boldsymbol{u}'}{\partial y} \right|_0 = \frac{u_\tau \boldsymbol{u}_\varDelta'}{l_s^+}.\end{equation}

Very recently, Hansen et al. (Reference Hansen, Whitmore, Abkart and Yang2022) have shown that very similar vertical profiles can be obtained from proper orthogonal decomposition analysis, showing that the most important (energetic) modes of the unresolved turbulence can be described by plug flow with a viscous layer towards the wall starting at $y^+ \sim 12$, consistent with our simple model.

Figure 3. A schematic of the turbNEQ velocity profiles resulting from two counter-rotating wall-attached eddies. Circles indicate the LES grid points, and the blue surface indicates a possible region of negative velocity fluctuation (green arrows) induced between wall-attached eddies (yellow) that can be only partially resolved on the LES resolution.

3. Wall-modelled LES for pulsating channel flow

Large-eddy simulations of pulsating channel flow, with an oscillating streamwise pressure gradient forcing, were conducted with the MTS wall model and with the classical EQWM. These results are compared with the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) upon which the simulation set-up is largely based. As in Weng et al. (Reference Weng, Boij and Hanifi2016), we adopt a triple decomposition where any variable, $F(\boldsymbol {x},t)$, may be written as

(3.1)\begin{equation} F(\boldsymbol{x},t) = \langle F \rangle_t(y) + \tilde{F}(y,t) + F'(\boldsymbol{x},t), \end{equation}

where $\langle F \rangle _t$ is the steady, time and horizontally averaged field, $\tilde {F}$ is the periodic component caused by the oscillatory pressure gradient, and $F'$ corresponds to turbulent fluctuations. Note that the turbulent fluctuations are the only cause for variability in the $x$ and $z$ directions for channel flow. Also note that a single prime in this section is not to be confused with a turbNEQ quantity unless specified otherwise. The time and horizontally averaged component is computed as

(3.2)\begin{equation} \langle F \rangle_t(y) = \frac{1}{(t_{N_t}-t_0) L_z L_x} \int_{t_0}^{t_{N_t}} \int_{0}^{L_z} \int_{0}^{L_x} F(\boldsymbol{x},t) \, \mathrm{d}\kern0.7pt x \, \mathrm{d} z \, \mathrm{d} t, \end{equation}

where $t_0$ and $t_{N_t}$ are the initial and final times, respectively, over which time averaging is done. The periodic component is found by subtracting the time-averaged flow field from the phase average:

(3.3)\begin{equation} \tilde{F} (y,t) \equiv \frac{1}{N_p L_x L_z} \sum_{n=1}^{N_p} \int_0^{L_z} \int_0^{L_x} F ( \boldsymbol{x}, t + (n-1) T_f ) \, {\rm d}\kern0.7pt x \, {\rm d}z - \langle F \rangle_t(y), \end{equation}

where $T_f$ is the pressure gradient forcing period, and $N_p$ is the total number of periods over which phase averaging is done.

Simulations are performed using LESGO (an open-source, mixed pseudo-spectral and finite difference code available on github, LESGO 2021) with a steady friction Reynolds number $\langle Re_\tau \rangle _t = u_{\tau p} h/\nu = 350$, where $h$ is the channel half-height, and $u_{\tau p} \equiv \sqrt {-h\rho ^{-1}(\partial _x \langle p \rangle _t)}$ is the friction velocity based on the steady pressure gradient. The Lagrangian scale-dependent dynamic subgrid stress model (Bou-Zeid et al. Reference Bou-Zeid, Meneveau and Parlange2005) is used in the bulk of the flow. The domain size, number of grid points and grid size are $(L_x, L_y, L_z)/h = (8{\rm \pi},2,3{\rm \pi} )$, $(N_x, N_y, N_z) = (128,30,48)$ and $(\varDelta _x, \varDelta _y, \varDelta _z)/h = (0.196,0.067,0.196)$, respectively. The third grid point is used for the wall-model height (i.e. $\varDelta = 5\varDelta _y/2$) because for low-Reynolds-number simulations, the first grid point falls beneath the log layer where the SGS model lacks accuracy. This underperformance causes an incorrect velocity to be fed into the wall model, which in turn produces an incorrect wall stress. Choosing a point further away allows a more accurately computed velocity to be fed into the wall model. It is also in agreement with the recommendations made by Larsson et al. (Reference Larsson, Kawai, Bodart and Bermejo-Moreno2016). Time advancement is done using an Adams–Bashforth method with a varying time step size to achieve a constant Courant–Friedrichs–Lewy (CFL) value 0.05. On average, this gives a time step size $\delta t \approx 4.2\times 10^{-4} h/u_{\tau p}$, which is two orders smaller than the fastest forcing time scale. This assures that all dynamics are well resolved temporally.

Sinusoidal flow variation is caused by the time-periodic streamwise pressure gradient forcing

(3.4)\begin{equation} \frac{\partial \langle p \rangle}{\partial x} = \frac{\partial \langle p \rangle_t}{\partial x}\,[ 1 + \beta \cos ( \omega_f t ) ], \end{equation}

where $\partial \langle p \rangle _t/\partial x$ is the steady pressure gradient forcing, and $\omega _f$ and $\beta$ are the pressure gradient forcing frequency and amplitude, respectfully. In our simulations, we use a sine function instead of a cosine function to avoid a discontinuous change in the pressure gradient forcing at $t=0$ when the forcing starts; however, we adopt the nomenclature of Weng et al. (Reference Weng, Boij and Hanifi2016) which uses a cosine function. Therefore, all phases reported are consistent with a cosine pressure gradient forcing. A wide range of forcing frequencies are tested, which cover the full range of possible flow types. This is summarized in table 1. The forcing frequency determines the extent to which the Stokes layer penetrates into the flow. Similarly, the Stokes length scale provides an estimate of this penetration depth and is related to the frequency through $l_f = \sqrt {2\nu /\omega _f}$ or in inner units $l_f^+ = \sqrt {2/\omega _f^+}$, where inner units normalization is done with the friction velocity $u_{\tau p}$ and the kinematic viscosity $\nu$. If the Stokes layer stays within the viscous sublayer, then it does not interact with the turbulence and the flow remains ‘quasi-laminar’. This is estimated to occur when $\omega _f^+>0.04$ or $l_f^+<7$ (Weng et al. Reference Weng, Boij and Hanifi2016). Several of the other frequencies tested are in the so-called ‘intermediate frequency range’ $0.006<\omega _f^+<0.04$, where the wall-stress amplitude is actually less than the amplitude from the Stokes solution. Finally, a couple of low-frequency cases are tested where the flow is in a quasi-steady state. In other words, the flow has time to adjust to the instantaneous pressure gradient.

Table 1. The forcing frequencies $\omega _f^+$ and periods and their corresponding Stokes lengths $l_f$ in inner units and outer units, and the flow regime classification. For comparison, the relevant wall-modelling time scales are $\langle T_s \rangle _t\,u_{\tau p}/h = 2.57$, $\langle t_\nu \rangle _t\,u_{\tau p}/h = 0.41$ and $\langle T_\varDelta \rangle _t\,u_{\tau p}/h = 0.83$.

Following Weng et al. (Reference Weng, Boij and Hanifi2016), the pressure gradient forcing amplitude is set to give a constant ratio for the periodic centreline velocity amplitude over the mean centreline velocity. This is done by fixing $a_{cl} \equiv |\tilde {u}_{cl}|/U_{cl} = 0.1$, where $U_{cl}$ is the centreline velocity of the laminar flow with the same flow rate as the turbulent mean flow. The relationship between $\beta$ and $a_{cl}$ can be determined by finding an analytical expression for the periodic centreline velocity $\tilde {u}_{cl}$. This is obtained by writing the momentum balance at the centre of the channel and then neglecting the total periodic stress – a valid assumption if the Stokes layer is far from the centre of the channel. The periodic centreline velocity is then found to be

(3.5)\begin{equation} \tilde{u}_{cl} = |\tilde{u}_{cl}| \cos (\omega_f t + \phi_{\tilde{u}_{cl}}), \end{equation}

where

(3.6a,b)\begin{equation} |\tilde{u}_{cl}| = \frac{\beta u_{\tau p}^2}{\omega_f h}, \quad \phi_{\tilde{u}_{cl}} ={-} {\rm \pi}/2.\end{equation}

Combining the amplitude shown in (3.6a,b) and the definition of $a_{cl}$, $\beta$ can be found using

(3.7)\begin{equation} \beta = a_{cl} \omega_f^+\,Re_{cl}, \end{equation}

where $Re_{cl}\equiv U_{cl}h/\nu \approx 9078$ for $Re_\tau = 350$, and $a_{cl}$ is set to a constant value $0.1$.

For the figures throughout this paper, the line types and colours of the various models/data have the following forms: DNS are shown with dashed black lines; LES with the MTS wall model are shown with solid black lines; and LES with the EQWM are shown with dashed-dot grey lines. For vertical profiles, open circles and plus symbols correspond to the location of LES grid points for LES with the MTS wall model and the EQWM, respectively. Extraneous lines, such as analytical laminar solutions, are shown with thin dotted lines. The different wall-stress components of the MTS wall model are shown with different colours: total wall stress is black, LaRTE wall stress is blue, lamNEQ wall stress is red, and turbNEQ wall stress is green.

Figure 4 shows the periodic centreline velocity for a wide range of pressure gradient forcing frequencies. For the intermediate and high frequencies, the LES are nearly indistinguishable from the DNS, whereas for $\omega _f^+ = 0.001, 0.003$, there are some discrepancies. These differences may be attributed to the LES overprediction of the mean velocity in the centre of the channel (see figure 5), which becomes important only for low frequencies when the Stokes layer interacts with the turbulence near the centre of the channel. However, for the intermediate and high frequencies, the centreline velocity agrees quite well with (3.5) and (3.6a,b), and the target periodic centreline velocity amplitude ($a_{cl}=0.1$) has been met.

Figure 4. The time evolution of the periodic centreline velocity $\tilde {u}_{cl}$ for several forcing frequencies, $\omega _f^+=0.001, 0.003, 0.006, 0.01, 0.02, 0.04$ (plots (a–f), respectively). Line types correspond to LES using the MTS wall model (thick solid black), LES using the EQWM (thick dashed-dot grey), and DNS from Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black). The phase within the cycle is based on the imposed pressure gradient forcing.

Figure 5. The time-averaged mean (a) velocity profiles and (b) Reynolds stresses. Dashed lines correspond to the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) for $Re_\tau =350$ with pulsations; circles with solid connecting lines correspond to LES with the MTS wall model; and plus symbols with dashed-dot connecting lines correspond to LES with the EQWM. In (b), $\langle u'u' \rangle _t$, $\langle v'v' \rangle _t$, $\langle w'w' \rangle _t$ and $\langle u'v' \rangle _t$ are shown with blue, red, green and black lines, respectively. For the LES, only the high-frequency case ($\omega _f^+=0.04$) is shown since the time-averaged velocity and Reynolds stress profiles are independent of the pulsation frequency.

Figure 5 shows the time-averaged mean velocity profiles and Reynolds stresses for the MTS wall model and for the EQWM compared with the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016). The MTS wall model and the EQWM give nearly identical first- and second-order statistics. This indicates that the mean behaviour of the LES is largely unaffected by the wall-model choice. As discussed in Fowler et al. (Reference Fowler, Zaki and Meneveau2022), there is a slight overshoot in the mean velocity profile in the wake region. However, this overshoot is attributed to simulation details other than the wall model, such as subgrid model and numerical effects. Additionally, for these low Reynolds number simulations, the SGS model tends to underpredict the subgrid stress beneath the log layer, thus leading to an overpredicted velocity. This is evident from the first grid point in figure 5. The Reynolds shear stress agrees well with DNS, as expected from momentum conservation, and the streamwise normal stress is also well predicted (except for the near-wall peak that is unresolved in LES). The spanwise and wall-normal diagonal Reynolds stress profiles are overpredicted by the LES, but in equal measure by all the wall models, pointing to remaining limitations of the SGS closure and not the wall models.

The governing equation for the periodic component of the streamwise velocity is found by subtracting the time-averaged streamwise momentum equation from the phase-averaged streamwise momentum equation:

(3.8)\begin{equation} \frac{\partial \tilde{u}}{\partial t} ={-}\frac{1}{\rho}\,\frac{\partial \tilde{p}}{\partial x} + \nu\,\frac{\partial^2 \tilde{u}}{\partial y^2} - \frac{\partial \widetilde{u'v'}}{\partial y}.\end{equation}

Laminar analytical solutions to (3.8) can be found by setting the Reynolds stress term to zero and using $\partial _x \tilde {p} = \beta (\partial _x \langle p \rangle _t) \cos (\omega _f t)$. The frequencies considered in table 1 are high enough such that the Stokes solution is similar to the laminar channel flow solution since $l_f \ll h$, as shown in table 1. Therefore we will simply use the Stokes solution as the ‘laminar channel flow solution’, which is

(3.9)\begin{equation} \tilde{u}/U_{cl} = a_{cl} [ \sin(\omega_f t) - {\rm e}^{{-}y/l_f}\sin(\omega_f t - y/l_f) ]. \end{equation}

Figure 6 shows the amplitude and phase of the periodic velocity for the six lowest forcing frequencies. The Stokes solution curve is also shown for reference. In the plots, it is clear that for the lowest frequency, the DNS and LES deviate from the Stokes solution significantly, thus a quasi-laminar state is not achieved. However, for the highest frequency shown, the DNS and LES follow the Stokes solution very closely, thus indicating that the flow is in a quasi-laminar state. Generally, the LES agree closely with the DNS. The MTS wall model and EQWM produce similar results, with the greatest discrepancies between the two occurring in the first few grid points away from the wall. These grid points are more sensitive to the wall model since they are affected more directly by the wall stress.

Figure 6. (a) Amplitude and (b) phase lead of the periodic velocity for six forcing frequencies, $\omega _f^+ = 0.001, 0.003, 0.006, 0.01, 0.02, 0.04$. The DNS of Weng et al. (Reference Weng, Boij and Hanifi2016), the LES with the MTS wall model, the LES with the EQWM, and the Stokes solution are shown with dashed black lines, open circles connected with solid black lines, grey plus symbols connected with grey dashed-dot lines, and dotted black lines, respectively. Animations of the periodic velocity can be accessed at https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-6/u_animation.html, and the corresponding source code can be found at https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-6/pulse_velocity_profiles.ipynb. Note that the animations of the DNS velocity profiles are computed from the provided amplitudes and phases.

Figures 7–10 show how the periodic wall stress changes with frequency, where figures 7 and 8 show the periodic wall-stress time signals, and figures 9 and 10 show the periodic wall-stress amplitude and phase as functions of frequency. Figure 7 compares LES with the MTS wall model (solid black lines) against the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (dashed black lines), and the LES with the EQWM (dashed-dot grey lines). The figure shows that the MTS wall model and EQWM perform similarly well for low frequencies, but as the frequency is increased, the EQWM degrades in performance, whereas the MTS wall model follows the trends of the DNS quite well. This is expected since the EQWM is based on equilibrium assumptions and therefore cannot capture properly the non-equilibrium dynamics of the high-frequency test cases. Figure 8 shows the different wall-stress contributions in the MTS wall model for the low, intermediate and high frequencies. This figure demonstrates why the MTS wall model can capture the trends of the DNS, and highlights the usefulness of such an approach. For the low, intermediate and high frequencies, the dominant contributors to the periodic wall stress are the quasi-equilibrium (LaRTE), turbNEQ and lamNEQ components, respectively. This is consistent with the length and time scale schematic in figure 1, where each component of the MTS wall model targets dynamics within a range of time scales. Using table 1, we see that the flow dynamics relative to the relaxation time scale (the frequencies in figure 8) are of the orders (a) $T_f/T_s \gg 1$, (b) $T_f/T_s \sim 1$ and (c) $T_f/T_s < 1$, which again is consistent with the model picture in figure 1. Note that in this flow, the scale separation between the laminar viscous time scale $t_\nu$ and the relaxation time scale $T_s$ is not very large (from the caption in table 1, we see that $\langle t_\nu \rangle _t/\langle T_s \rangle _t=0.16$). This is a direct result of the low Reynolds number of the flow considered. As seen from the expression $t_\nu /T_s = (l_s^+)^2/f(\varDelta ^+)\, \varDelta ^+$, the numerator is constant while typically, the denominator (and thus the scale ratio) increases with increasing Reynolds number.

Figure 7. Single-period time evolution of the periodic streamwise wall stress $\tilde {\tau }_{wx}$ for several forcing frequencies, $\omega _f^+=0.001, 0.003, 0.006, 0.01, 0.02, 0.04$ (plots (a–f), respectively). Line types correspond to LES using the MTS wall model (thick solid black), LES using the EQWM (thick dashed-dot grey), and DNS from Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black). The phase within the cycle is based on the imposed forcing frequency.

Figure 8. Single-period time evolution of the periodic streamwise wall stress $\tilde {\tau }_{wx}$ for low, intermediate and high forcing frequencies: $\omega _f^+=0.001, 0.006, 0.04$ (plots (a–c), respectively). Line types correspond to LES using the MTS wall model (thick solid black), with LaRTE (thin solid blue), lamNEQ (thin solid red) and turbNEQ (thin solid green) parts, and DNS from Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black). The phase within the cycle is based on the imposed forcing frequency.

Figure 9. (a) The periodic wall-stress amplitude normalized by the Stokes solution amplitude. (b) The periodic wall-stress phase relative to the centreline velocity phase. Asterisks correspond to outside experimental, LES or DNS data from Ronneberger & Ahrens (Reference Ronneberger and Ahrens1977) (experimental), Tardu et al. (Reference Tardu, Binder and Blackwelder1994) (experimental), Scotti & Piomelli (Reference Scotti and Piomelli2001) (LES) and Weng et al. (Reference Weng, Boij and Hanifi2016) (DNS). The DNS data of Weng et al. (Reference Weng, Boij and Hanifi2016) are emphasized with filled circles and connected with thick dashed black lines. LES using the MTS wall model are shown with open circles and connected with thick solid black lines. LES using the EQWM are shown with plus symbols and connected with thick dashed-dot grey lines. The thin dotted horizontal black lines correspond to the Stokes solution.

Figure 10. (a) The periodic wall-stress amplitude normalized by the Stokes solution. (b) The periodic wall-stress phase relative to the centreline velocity phase. Line types correspond to the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (filled circles connected with thick dashed black lines) and LES using the MTS wall model (open circles connected with thick solid black lines), with LaRTE (open circles connected with thick solid blue lines), lamNEQ (open circles connected with thick solid red lines), and turbNEQ (open circles connected with thick solid green lines) components. The thin dotted horizontal black lines correspond to the Stokes solution.

Figures 9 and 10 show the periodic wall-stress amplitude and phase. They provide the same information as figures 7 and 8, but in a more succinct manner, allowing trends to become more obvious. In general, as the forcing frequency increases, the wall-stress amplitude (normalized with the Stokes solution amplitude) decreases, and the wall-stress phase (relative to the centreline velocity phase) increases, until they reach their Stokes limit values 1 and 45 degrees, respectively. Figure 9 demonstrates clearly that the EQWM is unable to capture the non-equilibrium effects caused by the high-frequency pressure gradient pulsations. The wall-stress amplitude continues to decrease past its Stokes limit value, while the phase remains relatively constant. The MTS wall model, on the other hand, agrees quite well with DNS trends. It even captures the non-monotonic behaviour in the intermediate frequency range where the periodic wall-stress amplitude falls beneath the Stokes amplitude. The wall model's ability to capture the full spectrum of frequencies, from quasi-equilibrium conditions to Stokes limit conditions, is due to the separate modelling of quasi-equilibrium and non-equilibrium effects. This is observed most clearly in figure 10, where the model's decomposition into quasi-equilibrium, lamNEQ and turbNEQ parts is shown. The periodic wall stress, which is the wall-stress deviation from equilibrium conditions, is captured best by the LaRTE model for low frequencies, the lamNEQ model for high frequencies, and the turbNEQ model for intermediate frequencies (since the LaRTE and lamNEQ models become out of phase with each other). These models effectively turn on or off depending on if the conditions consistent with these models are met. This is an important quality to have to capture both extremes of non-equilibrium.

Figures 11–15 show the periodic Reynolds stresses as functions of height and phase for several forcing frequencies. In order to compare LES with DNS, the SGS stresses are included for the shear stress component, although the SGS contribution is negligible relative to the resolved stresses. Figure 11 shows $\widetilde {u'v'}$ profiles at different times (where time is indicated by a shift in the vertical direction), whereas figure 12 shows the $\widetilde {u'v'}$ amplitude and phase. For succinctness, only the amplitude and phase plots are shown for the normal stresses. Unlike the time-averaged Reynolds stress profiles in figure 5, the periodic Reynolds stresses for the wall-model LES do exhibit a dependency on the wall-model choice. For instance, in figure 12(c), the EQWM agrees well with the DNS, whereas the MTS wall model significantly underpredicts the amplitude. This discrepancy (for this particular frequency) is discussed further in detail below. Overall, the LES with the EQWM appear to agree with the DNS better than the MTS wall model for the $\widetilde {u'v'}$ and $\widetilde {u'u'}$ components; however, the reverse is true for the $\widetilde {v'v'}$ and $\widetilde {w'w'}$ components, where the EQWM tends to overpredict the amplitudes. It is interesting to note that the discrepancy between the MTS wall model and the EQWM is greatest for the intermediate frequencies and not for the highest frequency. This might be explained by the fact that for these frequencies, the Stokes length is roughly the same height as the height of the first LES grid point, which is the point that is most sensitive to the wall model.

Figure 11. The time evolution of $\widetilde {u'v'}$ at different phases of the wave cycle for different forcing frequencies: $\omega _f^+ = 0.001, 0.006, 0.01, 0.02, 0.04$. The profiles are $T_f/32$ apart, and are offset by $1\times 10^{-1}$ units in the vertical direction. Grey lines correspond to the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016). Black lines correspond to LES using the MTS wall model. Animations of the different periodic Reynolds stress components can be viewed by clicking on the links corresponding to the following frequencies: $\omega _f^+ = 0.001$, https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/rs_pul1_animation.html; $\omega _f^+ = 0.006$, https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/rs_pul3_animation.html; $\omega _f^+ = 0.01$, https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/rs_pul4_animation.html; $\omega _f^+ = 0.02$, https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/rs_pul5_animation.html; $\omega _f^+ = 0.04$, https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/rs_pul6_animation.html. The source code for generating these animations is located at https://www.cambridge.org/S0022112023005852/JFM-Notebooks/files/Figure-11/pulse_reynolds_stress_profiles.ipynb.

Figure 12. (a–e) Amplitude and ( f–j) phase lead of $\widetilde {u'v'}$ for five forcing frequencies, $\omega _f^+ = 0.001, 0.006, 0.01, 0.02, 0.04$. The DNS of Weng et al. (Reference Weng, Boij and Hanifi2016), the LES with the MTS wall model, and the LES with the EQWM are shown with dashed lines, open circles with solid black connecting lines, and plus signs with grey dashed-dot connecting lines, respectively.

The periodic Reynolds stress sensitivity to the wall model may be understood further by examining the different contributions to the phase-averaged, integrated momentum budget. These are related by

(3.10)\begin{equation} \int_0^y \frac{\partial \langle u \rangle}{\partial t}\,{{\rm d} y}' ={-}\frac{y}{\rho}\,\frac{\partial \langle p \rangle}{\partial x} + \nu\,\frac{\partial \langle u \rangle}{\partial y} - \langle u'v' \rangle - \langle \tau_{wx} \rangle,\end{equation}

where angled brackets represent phase averaging. Figure 16 shows the time signals of the different terms in (3.10) at three heights for the intermediate frequency $\omega _f^+ = 0.01$. Although the MTS wall model predicts the wall stress much better than the EQWM, small discrepancies in the $\partial _t \langle u \rangle$ term are correlated with noticeable discrepancies in the Reynolds stress since the Reynolds stress oscillation amplitude is small relative to the $\partial _t \langle u \rangle$ term. This figure highlights the intricate relationship between each term in the momentum balance. Instead of focusing on how a wall model might be able to capture these details (i.e. how wall-stress fluctuations can affect the near-wall turbulence), we give a greater focus on capturing the mean wall-stress behaviour, which is arguably the most important feature in wall modelling since an accurate skin friction prediction is usually the goal. We have shown in figures 7–10 that the MTS wall model is more successful than the EQWM at achieving this goal.

Figure 13. (a–e) Amplitude and ( f–j) phase lead of $\widetilde {u'u'}$ for five forcing frequencies $\omega _f^+ = 0.001, 0.006, 0.01, 0.02, 0.04$. Line types are the same as in figure 12.

Figure 14. (a–e) Amplitude and ( f–j) phase lead of $\widetilde {v'v'}$ for five forcing frequencies, $\omega _f^+ = 0.001, 0.006, 0.01, 0.02, 0.04$. Line types are the same as in figure 12.

Figure 15. (a–e) Amplitude and ( f–j) phase lead of $\widetilde {w'w'}$ for five forcing frequencies, $\omega _f^+ = 0.001, 0.006, 0.01, 0.02, 0.04$. Line types are the same as in figure 12.

Figure 16. Time signals of budget terms for $\omega _f^+=0.01$ in the integrated, phase-averaged $x$ momentum equation for different integration heights: (a) $y/h = 0.067$, (b) $y/h = 0.200$, and (c) $y/h = 0.467$. Line types correspond to the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (dashed lines), LES with the MTS wall model (solid lines), and LES with the EQWM (dashed-dot lines). Line colours correspond to different terms in the budget as indicated in the legend.

4. Wall-modelled LES for linearly accelerating channel flow

Wall-modelled LES were also conducted for a turbulent channel flow that is accelerated linearly over a ramp time $T$. The flow set-up is based on the DNS study of Jung & Kim (Reference Jung and Kim2017). In their work, the linear acceleration is imposed by modifying the pressure gradient forcing. The governing equation for the pressure gradient is found by integrating the ensemble-averaged streamwise momentum equation in the wall-normal direction over the entire channel. This yields

(4.1)\begin{equation} -\frac{1}{\rho}\,\frac{\partial \langle p \rangle^*}{\partial x}(t^*)=\frac{1}{2\, Re_{\tau,i}}\,\frac{\textrm{d} Re_m(t^*)}{\textrm{d} t^*}+\left(\frac{Re_\tau(t^*)}{Re_{\tau, i}}\right)^2, \end{equation}

where a star indicates normalization with $h$ and $u_{\tau p,i} \equiv \sqrt {-h\rho ^{-1}(\partial _x \langle p \rangle )_i}$ (the friction velocity based on the pressure gradient forcing before acceleration), $Re_{\tau,i} \equiv u_{\tau p,i} h/\nu$ is the initial friction Reynolds number, and $Re_m \equiv U_m2h/\nu$ is the bulk mean Reynolds number, with $U_m$ being the bulk mean velocity (averaged over the entire channel). Each term on the right-hand side of (4.1) is modelled since they are not known a priori. A benefit of this approach is that the pressure gradient remains unaffected by the LES wall model, and the LES have the exact same pressure gradient forcing as used in the DNS of Jung & Kim (Reference Jung and Kim2017). If $t^* = 0$ marks the beginning of the acceleration, then $Re_m$ is set according to

(4.2)$$\begin{gather} Re_m(t^*) = Re_{m,i}, \quad t^* < 0, \end{gather}$$

(4.3)$$\begin{gather}Re_m(t^*) = Re_{m,i} + \frac{t^*}{T^*}\, ( Re_{m,f} - Re_{m,i} ), \quad 0 \leq t^* < T^*, \end{gather}$$

(4.4)$$\begin{gather}Re_m(t^*) = Re_{m,f}, \quad t^* \geq T^*, \end{gather}$$

where the initial and final bulk mean Reynolds numbers $Re_{m,i}$ and $Re_{m,f}$, respectively, are estimated to give the correct initial and final friction Reynolds numbers. For all simulations considered in this study, the initial and final friction Reynolds numbers are $Re_{\tau,i}=180$ and $Re_{\tau,f}=395$ to match those of Jung & Kim (Reference Jung and Kim2017). Since these are low Reynolds numbers, following Jung & Kim (Reference Jung and Kim2017) we use the empirical relationship given by Dean (Reference Dean1978) to relate the bulk mean Reynolds number to the friction Reynolds number: $C_f \equiv \tau _w/\frac 12 U_m^2 \approx 0.073\,Re_m^{-1/4}$. To obtain $Re_{m,i}$ and $Re_{m,f}$ as functions of $Re_{\tau,i}$ and $Re_{\tau,f}$, respectively, we use $Re_m = (8/0.073)^{4/3}\,Re_\tau ^{8/3}$. Then once $Re_m(t)$ has been obtained from (4.2)–(4.4), we use the inverse relation $Re_\tau = (0.073/8)^{1/2}\,Re_m^{3/8}$ to substitute $Re_\tau (t)$ into (4.1) to obtain the pressure gradient forcing.

Table 2 shows the acceleration rates considered and their corresponding flow regimes. The flow regime classification is based on the work of Jung & Kim (Reference Jung and Kim2017) and the trends observed for the skin friction. A flow is considered ‘transitional’ if laminar-like behaviour is observed initially (e.g. through the skin friction) that breaks down into a new turbulent state as turbulent spots form. A flow is considered ‘quasi-steady’ if the skin friction does not deviate far from its steady value at a given flow rate (i.e. it agrees with ‘Dean's correlation’ specified above). The ‘intermediate’ flow does not exhibit transitional characteristics, yet its skin friction differs enough from its steady value that it cannot be labelled quasi-steady.

Table 2. The acceleration/ramp rates simulated, and the flow regime classification. For comparison, the relevant wall-modelling time scales are $T_s^* = 2.20$, $t_\nu ^*/h = 0.80$ and $T_\varDelta ^* = 1.22$, where the time scales are computed before the flow is accelerated (i.e. $t^* \leq 0$).

Large-eddy simulations were performed with the MTS wall model and compared against LES with the EQWM. The domain length, resolution and other simulation details are the same as the pulsatile channel flow, specified in § 3. Again, a constant CFL 0.05 was used, which gives an initial time step size $\delta t^* \approx 4.6\times 10^{-4}$, and a final time step size (long after the acceleration) $\delta t^* \approx 1.9\times 10^{-4}$. Note that the time step size decreases as the flow accelerates, to achieve a constant CFL. This time step size is several orders of magnitude smaller than the fastest acceleration rate, thus ensuring that all dynamics are well resolved temporally.

Figure 17 shows time signals of the imposed pressure gradient forcing and the resulting bulk mean Reynolds numbers for each of the acceleration rates. The pressure gradient forcing is designed to be the same between the LES and the DNS of Jung & Kim (Reference Jung and Kim2017), which is observed in figure 17(a). However, the mean Reynolds number is not controlled directly, so there can be discrepancies between the LES and DNS, which we see in figure 17(b). The acceleration rates match well between the DNS and the LES with largest deviations occurring for the slowest acceleration rate ($T^*=10$) at the end of the acceleration period. This is caused by a combination of factors, with the primary contributors being the performance of the wall model and the SGS model.

Figure 17. Time signals of (a) the pressure gradient forcing, and (b) the mean Reynolds number ($Re_m = 2 h U_m/\nu$) divided by the initial mean Reynolds number, $Re_{m,i}$, for different acceleration ramp rates. Ramp rates $T^* = 0.1, 1.0, 3.0, 5.0, 10.0$ correspond to black, blue, red, green and magenta lines, respectively. Line types for the DNS of Jung & Kim (Reference Jung and Kim2017), LES with the MTS wall model, and LES with the EQWM are dashed, solid and dashed-dot, respectively.

Figure 18 shows the mean velocity (figures 18a,c) and mean Reynolds stresses (figures 18b,d) before the acceleration (figures 18a,b) and long after the acceleration once the flow has reached its new steady-state (figures 18c,d). The LES and DNS agree reasonably well, with overall trends similar to those observed and discussed for the time-averaged profiles of pulsating channel flow (figure 5). Note that the slight overprediction of the velocity near the centre of the channel causes the overprediction of the mean Reynolds number after the acceleration period seen in figure 17(b).

Figure 18. The mean velocity profiles and Reynolds stresses (a,b) before acceleration and (c,d) after acceleration, once the flow has achieved its new steady state. Dashed lines correspond to the DNS of Moser, Kim & Mansour (Reference Moser, Kim and Mansour1999), circles with solid connecting lines correspond to LES with the MTS wall model, and plus signs with dashed-dot connecting lines correspond to LES with the EQWM. In (b,d), $\langle u'u' \rangle$, $\langle v'v' \rangle$, $\langle w'w' \rangle$ and $\langle u'v' \rangle$ are shown with blue, red, green and black lines, respectively.

Time signals of the planar-averaged wall stress for each of the acceleration rates considered are shown in figures 19 and 20. We first show the results in terms of the skin friction coefficient $C_f \equiv 2\tau _w/U_m^2$ in figure 19, in order to highlight the evolution during what is often termed a ‘turbulent to turbulent transition’. The acceleration process is marked by an initial fast increase in the skin friction, where a laminar Stokes layer develops; the skin friction then decays until the transition time, where (in the DNS) turbulent streaks would start developing and ultimately increase the skin friction to a new turbulent state at a higher Reynolds number. For example, He et al. (Reference He, Ariyaratne and Vardy2011) identify three acceleration stages for the wall stress with the following characteristics: (1) the turbulence remains ‘frozen’ and the wall stress is governed by a laminar solution; (2) the wall stress increases rapidly, with many signatures of a transition-like process; (3) the wall stress approaches its quasi-steady value asymptotically. Across each of these stages, the velocity deviation from its initial value (ensemble-averaged) is governed by the equation

(4.5)\begin{equation} \frac{\partial \langle u \rangle^\wedge}{\partial t} ={-}\frac{1}{\rho}\,\frac{\partial \langle p \rangle^\wedge}{\partial x} + \nu\, \frac{\partial^2 \langle u \rangle^\wedge}{\partial y^2} - \frac{\partial \langle u'v' \rangle^\wedge}{\partial y},\end{equation}

where angled brackets represents ensemble averaging, and $F^\wedge \equiv F(t) - F(t<0)$ (for any variable $F$) indicates the change in a variable from its initial value before the acceleration. Typically, the Reynolds shear stress deviation is neglected during the first stage because the turbulence is assumed to be ‘frozen’ (He et al. Reference He, Ariyaratne and Vardy2011). These arguments lead to a laminar solution to (4.5) (Sundstrom & Cervantes Reference Sundstrom and Cervantes2018c):

(4.6)\begin{equation} \langle u_{lam} \rangle^\wedge = U_m \left[ 1 - (1+2\eta^2)\,\textrm{erfc}(\eta) + \frac{2}{\sqrt{\rm \pi}}\,\eta\,\textrm{e}^{-\eta^2} \right], \quad \textrm{where} \ \eta = \frac{y}{\sqrt{4\nu t}}, \end{equation}

which has the corresponding wall stress

(4.7)\begin{equation} \langle \tau_{w,lam} \rangle^\wedge = 2 \frac{{\rm d}U_m}{{\rm d}t} \sqrt{\frac{\nu t}{\rm \pi}}.\end{equation}

The thin dotted line in figure 19 shows the laminar analytical solution during this initial acceleration stage (shifted to have initial wall stress $u_{\tau p,i}^2$). The DNS of Jung & Kim (Reference Jung and Kim2017) are shown with the thick dashed line. All acceleration rates have a brief period where DNS wall stress closely follows the laminar solution. However, for $T^*=0.1$ and $T^*=1$, the laminar solution persists longer (relative to the acceleration rate), and there is a distinctive time where the skin friction increases quickly, departing from this laminar state. This is a feature of stage 2, and is indicative of a transition-like process occurring. Jung & Kim (Reference Jung and Kim2017) identified these two acceleration rates as having a bypass-like transition. The rest of the acceleration rates are in a state of quasi-equilibrium where the wall stress does not differ far from its steady value at the instantaneous Reynolds number.

Figure 19. Time signals of the skin friction coefficient for different acceleration ramp rates. Ramp rates $T^* = 0.1, 1.0, 3.0, 5.0, 10.0$ correspond to plots (a–e), respectively. The curves compared are the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black line), LES with the EQWM (thick dashed-dot grey line), and LES with the MTS wall model (thick solid black line). The thin black dotted line is the laminar solution given by (4.7).

Figure 20. Time signals of the wall stress for different acceleration ramp rates. Ramp rates $T^* = 0.1, 1.0, 3.0, 5.0, 10.0$ correspond to plots (a–e), respectively. The curves compared are the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black line) and the LES with the MTS wall model (thick solid black line), with LaRTE (thick blue line), lamNEQ (thick red line) and turbNEQ (thick green line) components.

For the slowest acceleration case considered ($T^*=10$), the MTS wall model and the EQWM show little difference between them over the entirety of the acceleration. This trend is expected since the flow is in a state of quasi-equilibrium, and equilibrium assumptions made by the EQWM are a good approximation. Note that both LES skin frictions differ from the DNS long after the acceleration because of the overpredicted velocity in the wake region as seen in figure 18(c). For the faster acceleration rates, the EQWM performs very poorly relative to the DNS. The EQWM is unable to capture the quick increase in the skin friction caused by the developing laminar Stokes layer. The EQWM also overpredicts the skin friction once the flow starts transitioning to its new turbulent state. During this time, the EQWM incorrectly attributes the increase in velocity to an increase in the wall stress. This undesired effect justifies the use of a velocity correction in the equilibrium closure for the MTS wall model, as introduced in § 2.1.

The MTS wall model, on the other hand, does quite well over each of the acceleration rates considered. It is able to capture the wide range of flow features, from the rapid increase in $C_f$ initially, to the transition between turbulent states. Figure 20 shows the different contributions to the MTS wall stress so we may see clearly how each component behaves during the different stages of the flow. For all of the acceleration rates, the lamNEQ wall model is dominant when the flow first accelerates. This response allows the MTS wall model to capture the sharp initial increase in the wall stress, which the EQWM is unable to do. Conversely, the LaRTE wall model has a delayed response to the acceleration because of its inherent relaxation dynamics. Without the velocity correction, however, the LaRTE model responds too quickly, causing the wall stress to be overpredicted initially. Also as expected, after the flow has accelerated and approaches its new steady state, the LaRTE model is the primary contributor to the wall stress. In between these two extremes (after the lamNEQ contribution decays, but before the LaRTE model responds), the turbNEQ response is the most prominent. This also happens to be the time when the turbulent-to-turbulent transition occurs. Figures 20(a) and 20(b) show that the turbNEQ model helps to speed up the wall-stress response during this transition stage.

Further insights can be obtained by focusing on the relationship between the LES velocity at the wall-model point and the wall-stress evolution and fluctuations. According to the turbNEQ model (2.20) and (2.22), an increase in $\tau _{wx}'$ means that the LES velocity is increasing faster than the quasi-equilibrium velocity obtained from LaRTE, thus leading to a velocity deviation $u_\varDelta '$ (see figure 21 for time signals of this velocity as well as other model contributions to the LES velocity). For channel flow with a constant pressure gradient, this velocity deviation may be explained by turbulent fluctuations. However, for linearly accelerating channel flow, this velocity deviation has a non-zero average, which can be explained as follows. As the flow accelerates, the initial growth in $U_{LES}$ is accounted for by the laminar contribution $u_\varDelta ''$, and the turbulent contribution $u_\varDelta '$ is small. However, near the flow transition time, the laminar Stokes layer decays as it interacts with the ‘outside’ turbulence, and there is no change in the pressure gradient to drive its growth. This occurs at approximately the time $t=t_\nu$ since this time scale is defined as the time for a Stokes layer to grow from the wall to the edge of the laminar viscous sublayer. After this time, there is a difference between the turbulent state away from the wall and near the wall. In DNS studies, this leads to the generation of near-wall streaks and a breakdown to a new turbulent state (He & Seddighi Reference He and Seddighi2013, Reference He and Seddighi2015). In LES with the MTS wall model, this is measured through $u_\varDelta '$, and the turbNEQ model attempts to account for the expected increase in the wall stress during transition. In practice, the turbNEQ model responds less quickly than is desirable, as seen by the difference between the DNS and LES curves after transition in figure 20. A possible explanation is that the breakdown to turbulence caused by near-wall streak instabilities is a rapid phenomenon (Hack & Zaki Reference Hack and Zaki2014) that is not detected by the first LES velocity point, which is too far from the wall. The turbNEQ model relies solely on LES velocity information and therefore cannot account for this subtle effect whose modelling requires more detailed future efforts.

Figure 21. Time signals at a representative single point $(x,y,z)=(L_x/2,\varDelta,L_z/2)$ of the different modelling components of the LES velocity for several acceleration ramp rates. Ramp rates $T^* = 0.1, 1.0, 3.0, 5.0, 10.0$ correspond to plots (a–e), respectively. The different lines correspond to $U_{LES}$, $u_\tau f(\varDelta ^+)$, $u_\varDelta '$ and $u_\varDelta ''$, shown in grey, blue, green and red, respectively.

Single-point time signals (no planar averaging) of the different modelled components of the LES velocity are shown in figure 21. The LES velocity ($U_{LES}$ shown in grey) is decomposed according to (2.20), with LaRTE ($u_\tau f(\varDelta ^+)$, shown in blue), lamNEQ ($u_\varDelta '$, shown in red) and turbNEQ ($u_\varDelta ''$, shown in green) contributions. It is clear from the figure that the LaRTE portion effectively filters out the large LES velocity fluctuations due to the relaxation dynamics of LaRTE. It also captures the mean value before and after the linear acceleration. The lamNEQ portion captures the initial linear behaviour of the velocity as soon as the flow accelerates. The turbNEQ contribution is twofold. On the one hand, it is responsible for capturing the majority of the LES velocity fluctuations. On the other hand, it captures the behaviour of the velocity in response to transition, as discussed previously. Figure 21 demonstrates the usefulness of decomposing a complicated flow into its constitutive parts, as is possible with the MTS wall model.

Figure 22 shows time signals of the (planar-averaged) velocity perturbation at different heights for a fast acceleration case ($T^*=0.1$) and a slow acceleration case ($T^*=5$). For the fast acceleration case, the LES for both wall models gives the correct linear trend during the accelerating phase. However, after the acceleration is over, the LES predicts a decrease in the velocity perturbation too soon (with the exception of the channel centreline), with the EQWM generally giving a larger drop in the velocity perturbation than the MTS wall model, the latter therefore being closer to the DNS data. For the slow acceleration case, the LES and the DNS agree well over all times. This is expected since the flow is in a state of quasi-equilibrium and thus both wall models yield similar mean wall stresses.

Figure 22. Time signals of the velocity perturbation (from the initial condition) at several heights for (a) $T^*=0.1$ and (b) $T^*=5.0$. From light to dark lines, the heights correspond to $y/h = 0.167, 0.5, 0.967$, which are the third, eighth and centreline LES grid points, respectively. The DNS (from Jung & Kim Reference Jung and Kim2017), the LES with the MTS wall model, and the LES with the EQWM correspond to dashed lines with filled circles, solid lines, and dashed-dot lines, respectively. The circles correspond to the sample times given for the DNS.

5. The MTS wall model in the limit of instantaneous relaxation

A possible variant of the MTS wall model is now explored by considering the limit of a vanishingly small relaxation time scale, i.e. $T_s \to 0$. In that limit, the friction velocity from LaRTE is equal to its equilibrium value (i.e. ${\boldsymbol u}_\tau = \bar {\boldsymbol {\tau }}_w^{eq}/(\bar {\tau }_w^{eq})^{1/2}$, with the corresponding wall stress $u_\tau {\boldsymbol u}_\tau = \bar {\boldsymbol {\tau }}_w^{eq}$), and the quasi-equilibrium velocity becomes $\bar {\boldsymbol u}_\varDelta = {\boldsymbol u}_\tau \,f(\varDelta ^+)$, since ${\boldsymbol u}_\tau$ is obtained from the equilibrium model that uses $\bar {\boldsymbol u}_\varDelta$ as input velocity. Therefore, according to (2.20), $\boldsymbol {u}'_\varDelta = 0$ and the turbulent turbNEQ portion is subsumed into the equilibrium wall-model contribution. The total wall stress for the MTS wall model in the limit $T_s \to 0$ is then simply

(5.1)\begin{equation} \boldsymbol{\tau}_w = \bar{\boldsymbol{\tau}}_w^{eq} + \boldsymbol{\tau}_{w}'',\end{equation}

where $\bar {\boldsymbol {\tau }}_w^{eq}$ is evaluated according to the fit from (2.13), and $\boldsymbol {\tau }_{w}''$ is governed by (2.18). The MTS wall model in the limit of instantaneous relaxation, governed by (5.1), is referred to as the equilibrium MTS (EQMTS) wall model. It is important to note that the quasi-equilibrium velocity input still contains the velocity correction to the LES velocity ((2.14) and (2.15)) to account for changes in the LES velocity caused by the laminar Stokes layer. For succinctness, the equilibrium model component $\bar {\boldsymbol {\tau }}_w^{eq}$ with a corrected velocity input is referred to as the ‘corrected equilibrium’ model.

We now apply this model to pulsating and linearly accelerating channel flow. Representative resulting stress evolution plots are shown in figures 23–25. For pulsating channel flow, the EQMTS wall model is nearly identical to the EQWM for the two lowest frequencies ($\omega _f^+ = 0.001, 0.003$). For low frequencies, the lamNEQ contribution is relatively small, meaning that the corrected equilibrium wall stress is dominant. Additionally, while $T_f \gg T_\varDelta$, the velocity correction has a negligible impact and the corrected equilibrium wall model thus behaves similarly to the standard EQWM (e.g. see figure 24(a) where the corrected equilibrium wall-stress component and EQWM curves are nearly indistinguishable). These two effects cause the EQMTS wall model to behave similarly to the EQWM for low frequencies where performance is good.

Figure 23. Single-period time evolution of the periodic streamwise wall stress $\tilde {\tau }_{wx}$ for several forcing frequencies, $\omega _f^+=0.001, 0.003, 0.006, 0.01, 0.02, 0.04$ (plots (a–f), respectively). Line types correspond to LES using the MTS wall model (thick solid black), LES using the EQWM (thick dashed-dot grey), LES using the equilibrium MTS wall model (thick dotted black) and DNS from Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black). The phase within the cycle is based on the imposed forcing frequency.

Most evident in figure 23(d), the total EQMTS wall stress is not sinusoidal. From figure 24, we see that this is caused by the corrected equilibrium model component, which becomes non-sinusoidal as frequency is increased. This must be caused by the velocity correction since this is the only difference between the corrected equilibrium and EQWM models. The model (2.14) shows that $\boldsymbol {u}_\varDelta ''$ evolves at time scale $T_\varDelta$. When subtracted from the LES velocity (which evolves at the forcing period $T_f$), the quasi-equilibrium velocity input becomes distorted and non-sinusoidal if $T_f$ and $T_\varDelta$ are of similar order. This occurs in the intermediate- and high-frequency regimes.

For high frequencies, the EQMTS wall model behaves similar to the regular MTS wall model. This is primarily because the lamNEQ model is dominant here, which is shared between the two models and therefore any differences between the corrected equilibrium model and the LaRTE+turbNEQ stresses (figure 24c) are small relative to the total wall stress. At high frequencies ($\omega _f^+ \geq 0.04$), the velocity correction effectively filters out the corresponding high frequency content of the LES velocity, which causes the equilibrium portion of the equilibrium MTS wall model to respond slowly, similarly to the LaRTE model. Without the velocity correction, the total wall stress for the EQMTS wall model is simply the lamNEQ wall stress plus the EQWM wall stress. This leads to an overprediction of the total wall stress, thus showing the necessity of the velocity correction for non-equilibrium flows.

Figure 24. Single-period time evolution of the periodic streamwise wall stress $\tilde {\tau }_{wx}$ for low, intermediate and high forcing frequencies, $\omega _f^+=0.001, 0.006, 0.04$ (plots (a–c), respectively). Curves shown include the corrected equilibrium component of the EQMTS wall model (dotted blue), the EQWM wall stress (dashed-dot grey), and the LaRTE+turbNEQ wall stresses (solid cyan). The phase within the cycle is based on the imposed forcing frequency.

Figure 25. Time signals of the skin friction coefficient for different acceleration ramp rates. Ramp rates $T^* = 0.1, 1.0, 3.0, 5.0, 10.0$ correspond to plots (a–e), respectively. The curves compared are the DNS of Weng et al. (Reference Weng, Boij and Hanifi2016) (thick dashed black line), LES with the EQWM (thick dashed-dot grey line), LES with the EQMTS wall model (thick dotted black line), and LES with the MTS wall model (thick solid black line). The thin black dotted line is the laminar solution given by (4.7).

For linearly accelerating channel flow, the EQMTS wall model is able to achieve some of the same trends in the skin friction as the full MTS wall model (e.g. the sharp increase in the skin friction initially), although it tends to overpredict the skin friction after the laminar stage of the acceleration. The velocity correction allows the EQMTS model to have a delayed response to changes in the pressure gradient so that the lamNEQ model can capture the non-equilibrium response to fast changes in the pressure gradient. However, the velocity correction time scale $T_\varDelta$ appears to not be long enough for the EQMTS wall model to give the correct wall stress since the skin friction begins to increase too early for all of the acceleration rates shown in figure 25. In fact, the EQMTS wall stress even exceeds the EQWM wall stress during portions of the flow acceleration for the slow acceleration cases. This must be caused by the slow decay of the lamNEQ wall stress since the corrected equilibrium wall stress $\bar {\boldsymbol {\tau }}_w^{eq}$ can never be greater than the EQWM wall stress (since it is essentially just a delayed version of it).

We now comment briefly on the differences in computational cost between the wall models considered. For all wall-modelled LES considered here, the computational cost remains insignificant compared to wall-resolved LES because the wall models do not require solving equations on a fine, near-wall mesh (see e.g. Choi & Moin (Reference Choi and Moin2012) and Yang & Griffin (Reference Yang and Griffin2021) for more details). For pulsatile channel flow, the average percentage of time spent in the wall-model function call (over the total time spent per time step) was measured to be 18.973 % for the MTS wall model, 16.373 % for the EQMTS wall model, and 3.390 % for the EQWM. Similar percentages were found for the linearly accelerating channel flow. The $\sim$3 % of time spent for the EQWM is consistent with expectations since 30 grid points were used in the wall-normal direction, and wall model computations are done over a single horizontal plane. The additional $\sim$15 % of time spent for the MTS and EQMTS wall models is a direct result of the additional 48 exponential terms (per point on the horizontal wall-modelling plane) needed for the lamNEQ model. This increase in cost is expected since $N_{exp}$ times more computations were used for the lamNEQ model. However, it is clear from the present results that the lamNEQ model plays a critical role in properly modelling the wall stress in instances of high non-equilibrium, therefore no effort was made to reduce $N_{exp}$ to decrease the computational cost. It is possible that further gains in efficiency could be made by reducing $N_{exp}$ following a careful study of loss of accuracy versus computational efficiency. In this work, we opted to keep the model highly accurate since the overall cost increase was relatively small. Finally, the minor difference in cost between the MTS and EQMTS wall models shows that the additional complexity of the LaRTE model does not equate with a significant increase in computational time.

Overall, the EQMTS wall model is able to capture several of the important features in non-equilibrium flows (since the lamNEQ model captures the majority of these dynamics) while maintaining some of the simplicity of the EQWM. While the full MTS model agrees somewhat better with the DNS for the majority of the non-equilibrium flows tested, the EQMTS wall model can be considered as a simpler alternative since it does not require the solution of the LaRTE friction-velocity transport equation.