Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-03T00:38:13.941Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiscale analysis of the topological invariants in the logarithmic region of turbulent channels at a friction Reynolds number of 932

Published online by Cambridge University Press:  30 August 2016

A. Lozano-Durán ,
M. Holzner  and
J. Jiménez
A. Lozano-Durán*
Affiliation:
Center for Turbulence Research, Stanford University, Stanford, CA 94305, USA
M. Holzner
Affiliation:
ETH Zurich, 8093 Zurich, Switzerland
J. Jiménez
Affiliation:
School of Aeronautics, U. Politécnica de Madrid, 28040 Madrid, Spain
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

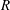The invariants of the velocity gradient tensor, $R$ and 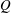$Q$, and their enstrophy and strain components are studied in the logarithmic layer of an incompressible turbulent channel flow. The velocities are filtered in the three spatial directions and the results are analysed at different scales. We show that the 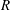$R$–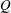$Q$ plane does not capture the changes undergone by the flow as the filter width increases, and that the enstrophy/enstrophy-production and strain/strain-production planes represent better choices. We also show that the conditional mean trajectories may differ significantly from the instantaneous behaviour of the flow since they are the result of an averaging process where the mean is 3–5 times smaller than the corresponding standard deviation. The orbital periods in the 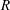$R$–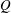$Q$ plane are shown to be independent of the intensity of the events, and of the same order of magnitude as those in the enstrophy/enstrophy-production and strain/strain-production planes. Our final goal is to test whether the dynamics of the flow is self-similar in the inertial range, and the answer turns out to be that it is not. The mean shear is found to be responsible for the absence of self-similarity and progressively controls the dynamics of the eddies observed as the filter width increases. However, a self-similar behaviour emerges when the calculations are repeated for the fluctuating velocity gradient tensor. Finally, the turbulent cascade in terms of vortex stretching is considered by computing the alignment of the vorticity at a given scale with the strain at a different one. These results generally support a non-negligible role of the phenomenological energy-cascade model formulated in terms of vortex stretching.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 356 - 394
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30 (8), 2343–2353.Google Scholar
Atkinson, C., Chumakov, S., Bermejo-Moreno, I. & Soria, J. 2012 Lagrangian evolution of the invariants of the velocity gradient tensor in a turbulent boundary layer. Phys. Fluids 24 (10), 105104.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199 (1057), 238–255.Google Scholar
Beck, C. & Schögl, F. 1993 Thermodynamics of Chaotic Systems. Cambridge University Press.Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.CrossRefGoogle Scholar
Borue, V. & Orszag, S. A. 1998 Local energy flux and subgrid-scale statistics in three-dimensional turbulence. J. Fluid Mech. 366, 1–31.CrossRefGoogle Scholar
van der Bos, F., Tao, B., Meneveau, C. & Katz, J. 2002 Effects of small-scale turbulent motions on the filtered velocity gradient tensor as deduced from holographic particle image velocimetry measurements. Phys. Fluids 14 (7), 2456–2474.Google Scholar
Cantwell, B. J. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids 4 (4), 782–793.CrossRefGoogle Scholar
Cardesa, J., Vela-Martín, A., Dong, S. & Jiménez, J. 2015 The propagation of kinetic energy across scales in turbulent flows. Phys. Fluids 27 (11), 111702.Google Scholar
Cardesa, J. I., Mistry, D., Gan, L. & Dawson, J. R. 2013 Invariants of the reduced velocity gradient tensor in turbulent flows. J. Fluid Mech. 716, 597–615.CrossRefGoogle Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.Google Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11 (8), 2394–2410.Google Scholar
Chevillard, L., Lvque, E., Taddia, F., Meneveau, C., Yu, H. & Rosales, C. 2011 Local and nonlocal pressure Hessian effects in real and synthetic fluid turbulence. Phys. Fluids 23 (9).Google Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97, 174501.Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20 (10).Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of three-dimensional flow fields. Phys. Fluids 2 (5), 765–777.Google Scholar
Chong, M. S., Soria, J., Perry, A. E., Chacin, J., Cantwell, B. J. & Na, Y. 1998 Turbulence structures of wall-bounded shear flows found using DNS data. J. Fluid Mech. 357, 225–247.Google Scholar
Corrsin, S.1958 Local isotropy in turbulent shear flow. NACA Res. Memo 58B11.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Doi, M. & Edwards, S. F. 1988 The Theory of Polymer Dynamics. Clarendon Press.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 015102.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22 (7), 071704.Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.CrossRefGoogle Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Local and nonlocal strain rate fields and vorticity alignment in turbulent flows. Phys. Rev. E 77, 026303.Google Scholar
Jiménez, J. 1992 Kinematic alignment effects in turbulent flows. Phys. Fluids 4 (4).CrossRefGoogle Scholar
Jiménez, J. 2000 Intermittency and cascades. J. Fluid Mech. 409, 99–120.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25, 110814.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kim, J., Moin, P. & Moser, R. D. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Lehew, J. A., Guala, M. & Mckeon, B. J. 2013 Time-resolved measurements of coherent structures in the turbulent boundary layer. Exp. Fluids 54 (4), 1–16.Google Scholar
Leung, T., Swaminathan, N. & Davidson, P. A. 2012 Geometry and interaction of structures in homogeneous isotropic turbulence. J. Fluid Mech. 710, 453–481.Google Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Meneveau, C., Burns, Randal, C., Shiyi, S., Alexander & E., Gregory 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turb. 9, N31.Google Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.Google Scholar
Lozano-Durán, A., Holzner, M. & Jiménez, J. 2015 Numerically accurate computation of the conditional trajectories of the topological invariants in turbulent flows. J. Comput. Phys. 295, 805–814.CrossRefGoogle Scholar
Lozano-Durán, A. & Jiménez, J. 2014a Effect of the computational domain on direct simulations of turbulent channels up to Re 𝜏 = 4200. Phys. Fluids 26 (1), 011702.Google Scholar
Lozano-Durán, A. & Jiménez, J. 2014b Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.Google Scholar
Lüthi, B., Holzner, M. & Tsinober, A. 2009 Expanding the Q–R space to three dimensions. J. Fluid Mech. 641, 497–507.CrossRefGoogle Scholar
Lüthi, B., Ott, S., Berg, J. & Mann, J. 2007 Lagrangian multi-particle statistics. J. Turb. 8, N45.Google Scholar
Martín, J., Ooi, A., Chong, M. S. & Soria, J. 1998 Dynamics of the velocity gradient tensor invariants in isotropic turbulence. Phys. Fluids 10 (9), 2336–2346.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43 (1), 219–245.Google Scholar
Moisy, F. & Jiménez, J. 2004 Geometry and clustering of intense structures in isotropic turbulence. J. Fluid Mech. 513, 111–133.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.Google Scholar
Mullin, J. A. & Dahm, W. J. A. 2006 Dual-plane stereo particle image velocimetry measurements of velocity gradient tensor fields in turbulent shear flow. II: experimental results. Phys. Fluids 18 (3).Google Scholar
Naso, A. & Pumir, A. 2005 Scale dependence of the coarse-grained velocity derivative tensor structure in turbulence. Phys. Rev. E 72, 056318.Google ScholarPubMed
Naso, A., Pumir, A. & Chertkov, M. 2006 Scale dependence of the coarse-grained velocity derivative tensor: influence of large-scale shear on small-scale turbulence. J. Turb. 7, N41.CrossRefGoogle Scholar
Naso, A., Pumir, A. & Chertkov, M. 2007 Statistical geometry in homogeneous and isotropic turbulence. J. Turb. 8, N39.Google Scholar
Ooi, A., Martín, J., Soria, J. & Chong, M. S. 1999 A study of the evolution and characteristics of the invariants of the velocity-gradient tensor in isotropic turbulence. J. Fluid Mech. 381, 141–174.CrossRefGoogle Scholar
Pumir, A. & Naso, A. 2010 Statistical properties of the coarse-grained velocity gradient tensor in turbulence: Monte–Carlo simulations of the tetrad model. New J. Phys. 12 (12), 123024.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1991 Structure and dynamics of homogeneous turbulence: models and simulations. Proc. R. Soc. Lond. A 434 (1890), 101–124.Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.Google Scholar
Tanahashi, M., Kang, S., Miyamoto, T. & Shiokawa, S. 2004 Scaling law of fine scale eddies in turbulent channel flows up to Re 𝜏 = 800. Intl J. Heat Fluid Flow 25, 331–341.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Tsinober, A. 1998 Is concentrated vorticity that important? Eur. J. Mech. (B/Fluids) 17 (4), 421–449.Google Scholar
Tsinober, A., Shtilman, L. & Vaisburd, H. 1997 A study of properties of vortex stretching and enstrophy generation in numerical and laboratory turbulence. Fluid Dyn. Res. 21 (6), 477–494.CrossRefGoogle Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. France 43 (6), 837–842.CrossRefGoogle Scholar
Vieillefosse, P. 1984 Internal motion of a small element of fluid in an inviscid flow. Phys. Stat. Mech. Appl. 125 (1), 150–162.Google Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.Google Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Wang, L. & Lu, X.-Y. 2012 Flow topology in compressible turbulent boundary layer. J. Fluid Mech. 703, 255–278.Google Scholar