Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Furquan, Mohd
and
Mittal, Sanjay
2021.
Flow-induced vibration of filaments attached to two side-by-side cylinders.
Physics of Fluids,
Vol. 33,
Issue. 6,
Bao, Bin
Wang, Quan
Wu, Yufei
and
Li, Pengda
2021.
Experimental Study on Hydroelectric Energy Harvester Based on a Hybrid Qiqi and Turbine Structure.
Energies,
Vol. 14,
Issue. 22,
p.
7601.
Manjunathan, Sujyesh Aanandh
and
Borazjani, Iman
2022.
Flow-induced vibration of a circular cylinder with an attached elastic plate of high aspect ratio.
Physics of Fluids,
Vol. 34,
Issue. 11,
Mao, Qian
Liu, Yingzheng
and
Sung, Hyung Jin
2022.
Drag reduction by flapping a flexible filament behind a stationary cylinder.
Physics of Fluids,
Vol. 34,
Issue. 8,
He, Tao
2022.
Modeling fluid–structure interaction with the edge-based smoothed finite element method.
Journal of Computational Physics,
Vol. 460,
Issue. ,
p.
111171.
Furquan, Mohd
and
Mittal, Sanjay
2023.
Vortex-induced vibration and flutter of a filament behind a circular cylinder.
Theoretical and Computational Fluid Dynamics,
Vol. 37,
Issue. 3,
p.
305.
Shukla, S.
Govardhan, R.N.
and
Arakeri, J.H.
2023.
Flow over a circular cylinder with a flexible splitter plate.
Journal of Fluid Mechanics,
Vol. 973,
Issue. ,
Pandey, Avinash Kumar
Sharma, Gaurav
and
Bhardwaj, Rajneesh
2023.
Flow-induced reconfiguration and cross-flow vibrations of an elastic plate and implications to energy harvesting.
Journal of Fluids and Structures,
Vol. 122,
Issue. ,
p.
103977.
Chen, Zepeng
Mao, Qian
Liu, Yingzheng
and
Sung, Hyung Jin
2023.
Snap-through dynamics of a buckled flexible filament with different edge conditions.
Physics of Fluids,
Vol. 35,
Issue. 10,
Sahu, Tulsi Ram
Furquan, Mohd
and
Mittal, Sanjay
2023.
Symmetry-breaking response of a flexible splitter plate attached to a circular cylinder in uniform flow.
Physics of Fluids,
Vol. 35,
Issue. 12,
Mao, Qian
Liu, Yingzheng
and
Sung, Hyung Jin
2023.
Drag reduction by flapping a pair of flexible filaments behind a cylinder.
Physics of Fluids,
Vol. 35,
Issue. 3,
Zhang, Jiaxiang
Wang, Fujun
Zhang, Jinya
Chen, Dongyang
and
Liu, Zongku
2023.
Vortex-induced vibration characteristics of three cylinders with isosceles-triangle arrangements at low Reynolds number.
Physics of Fluids,
Vol. 35,
Issue. 12,
Mao, Qian
Liu, Yingzheng
and
Sung, Hyung Jin
2023.
Snap-through dynamics of a buckled flexible filament in a uniform flow.
Journal of Fluid Mechanics,
Vol. 969,
Issue. ,
Chatterjee, Rajanya
Shah, Chhote Lal
Gupta, Sayan
and
Sarkar, Sunetra
2024.
Energy harvesting from wake-induced vibration of flexible flapper behind a bluff body.
Physics of Fluids,
Vol. 36,
Issue. 11,
Zhang, Ziqiang
Yin, Yapeng
and
Wang, Hanfeng
2024.
Control of the nonlinear flutter of a rectangular cylinder using auxiliary flexible films.
Nonlinear Dynamics,
Vol. 112,
Issue. 18,
p.
15741.
Li, Guojun
Jaiman, Rajeev Kumar
Lei, Biao
and
Liu, Hongzhong
2024.
Wake interference effects on flow-induced vibration of flexible membrane wings.
Physics of Fluids,
Vol. 36,
Issue. 7,
Giri, Shubham
Kartik, V.
Agrawal, Amit
and
Bhardwaj, Rajneesh
2024.
Measurements of flow-induced vibration of a flexible splitter plate mounted on a cylinder in free stream flow.
Physics of Fluids,
Vol. 36,
Issue. 1,
Li, Guojun
Zhang, Haichun
Lei, Biao
Wang, Lanlan
Jiang, Weitao
and
Liu, Hongzhong
2024.
Enhancing stability and performance of flexible membrane structures in wake flows through jet flow control.
Ocean Engineering,
Vol. 313,
Issue. ,
p.
119366.
Amini, Yasser
and
Zahed, Iman
2024.
Effects of attached flexible splitter plates on flow-induced vibration of two tandem circular cylinders: Two-degree of freedoms study.
Ocean Engineering,
Vol. 296,
Issue. ,
p.
116762.
Chen, Zepeng
Liu, Yingzheng
and
Sung, Hyung Jin
2024.
Flow-induced oscillations of an S-shaped buckled flexible filament.
Journal of Fluid Mechanics,
Vol. 1000,
Issue. ,
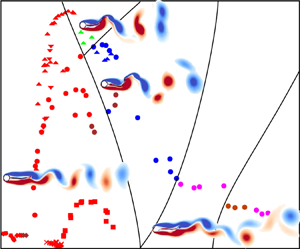
 $\mathsf {2P+2S}$ mode. The modes of shedding show a systematic variation with amplitude and frequency. The map of vortex-shedding patterns in the amplitude–frequency plane resembles the corresponding map for forced vibration of a rigid cylinder. The transformation of wake from one mode of shedding to another is explained phenomenologically. Variation of rate of energy transfer between the fluid and filament with space and time is analysed to determine optimal placement of transducers for harvesting energy.
$\mathsf {2P+2S}$ mode. The modes of shedding show a systematic variation with amplitude and frequency. The map of vortex-shedding patterns in the amplitude–frequency plane resembles the corresponding map for forced vibration of a rigid cylinder. The transformation of wake from one mode of shedding to another is explained phenomenologically. Variation of rate of energy transfer between the fluid and filament with space and time is analysed to determine optimal placement of transducers for harvesting energy.