Published online by Cambridge University Press: 27 June 2023
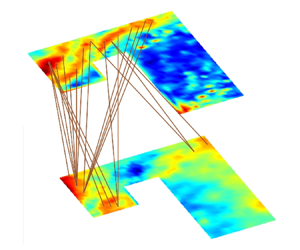
Thermoacoustic systems are complex systems where the interactions between the hydrodynamic, acoustic and heat release rate fluctuations lead to diverse dynamics such as chaos, intermittency and ordered dynamics. Such complex interactions cause catastrophically high-amplitude acoustic pressure oscillations and the emergence of order in the spatiotemporal dynamics, referred to as thermoacoustic instability. In this work, we use multilayer networks to study the spatial pattern of inter-subsystem interactions between the vorticity dynamics and thermoacoustic power generated due to acoustically coupled combustion in a bluff-body-stabilised turbulent dump combustor. We construct a two-layered network where the layers represent the thermoacoustic power and vorticity fields. The inter-layer links are determined using cross-variable short-window correlations between vorticity and thermoacoustic power fluctuations at any two locations in the flow field. Analysing the topology of inter-layer networks, using network properties such as degree correlations and link-rank distributions, helps us infer the spatial inhomogeneities in inter-subsystem interactions and unravel the fluid mechanical processes involved during different dynamical states. We show that, during chaotic dynamics, interactions between subsystems are non-localised and spread throughout the flow field of the combustor. During the state of thermoacoustic instability (order), we find that intense interactions occur in between regions of coherent vortex shedding and thermoacoustic power generation and we understand that these processes are strongly and locally coupled. Moreover, we discover that such dense inter-layer connections emerge in spatial pockets in the dump plane of the combustor during the state of intermittency much prior to the onset of order.