Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-09T21:58:13.291Z Has data issue: false hasContentIssue false
  • English
  • Français

A multi-layer model for nonlinear internal wave propagation in shallow water

Published online by Cambridge University Press:  09 February 2012

Philip L.-F. Liu  and
Xiaoming Wang
Philip L.-F. Liu*
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA Institute of Hydrological and Oceanic Sciences, National Central University, Jhongli, Taoyuan 32001, Taiwan
Xiaoming Wang
Affiliation:
School of Civil and Environmental Engineering, Cornell University, Ithaca, NY 14853, USA GNS Science, Wairakei 3377, New Zealand
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, a multi-layer model is developed for the purpose of studying nonlinear internal wave propagation in shallow water. The methodology employed in constructing the multi-layer model is similar to that used in deriving Boussinesq-type equations for surface gravity waves. It can also be viewed as an extension of the two-layer model developed by Choi & Camassa. 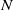The multi-layer model approximates the continuous density stratification by an -layer fluid system in which a constant density is assumed in each layer. This allows the model to investigate higher-mode internal waves. Furthermore, the model is capable of simulating large-amplitude internal waves up to the breaking point. However, the model is limited by the assumption that the total water depth is shallow in comparison with the wavelength of interest. Furthermore, the vertical vorticity must vanish, while the horizontal vorticity components are weak. Numerical examples for strongly nonlinear waves are compared with laboratory data and other numerical studies in a two-layer fluid system. Good agreement is observed. The generation and propagation of mode-1 and mode-2 internal waves and their interactions with bottom topography are also investigated.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Shallow water flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 695 , 25 March 2012 , pp. 341 - 365
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Apel, J. R., Badiey, M., Chiu, C.-S., Finette, S., Headrick, R., Kemp, J., Lynch, J. F., Newhall, A., Orr, M. H., Pasewark, B. H., Tielbuerger, D., Turgut, A., von der Heydt, K. & Wolf, S. 1997 An overview of the 1995 SWARM shallow-water internal wave acoustic scattering experiment. IEEE J. Ocean. Engng 22, 465–500.CrossRefGoogle Scholar
2. Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
3. Bole, J. B., Ebbesmeyer, C. C. & Romea, R. D. 1994 Soliton currents in the South China Sea: measurements and theoretical modelling. In Proceedings of the 26th Annual Offshore Technology Conference, Houston, TX, 1994, pp. 367–376.Google Scholar
4. Camassa, R., Choi, W., Michallet, H., Rusas, R.-O. & Sveen, J. K. 2006 On the realm of validity of strongly nonlinear asymptotic approximations for internal waves. J. Fluid Mech. 549, 1–23.CrossRefGoogle Scholar
5. Chao, S.-Y., Shaw, P.-T., Hsu, M.-K. & Yang, Y.-J. 2006 Reflection and diffraction of internal solitary waves by a circular island. J. Oceanogr. 62, 811–823.CrossRefGoogle Scholar
6. Chen, Y. & Liu, P. L.-F. 1995 The unified Kadomtsev–Petviashvili equation for interfacial waves. J. Fluid Mech. 288, 383–408.CrossRefGoogle Scholar
7. Choi, W. 2000 Modeling of strongly nonlinear internal gravity waves. In Proceedings of 4th International Conference on Hydrodynamics, Yokohama, Japan, pp. 453–458.Google Scholar
8. Choi, W. & Camassa, R. 1996 Weakly nonlinear internal waves in a two-fluid system. J. Fluid Mech. 313, 83–103.CrossRefGoogle Scholar
9. Choi, W. & Camassa, R. 1999 Fully nonlinear internal waves in a two-fluid system. J. Fluid Mech. 396, 1–36.CrossRefGoogle Scholar
10. Davis, R. E. & Acrivos, A. 1967 Solitary internal waves in deep water. J. Fluid Mech. 29, 593–607.CrossRefGoogle Scholar
11. Debsarma, S., Das, K. P. & Kirby, J. T. 2010 Fully nonlinear higher-order model equations for long internal waves in a two-fluid system. J. Fluid Mech. 654, 281–303.CrossRefGoogle Scholar
12. Duda, T. F., Lynch, J. F., Irish, J. D., Beardsley, R. C., Ramp, S.R., Chiu, C.-S., Tang, T. Y. & Yang, Y.-J. 2004 Internal tide and nonlinear wave behavior in the continental slope in the northern South China Sea. IEEE J. Ocean. Engng 29, 1105–1131.CrossRefGoogle Scholar
13. Evans, W. A. & Ford, M. J. 1996 An integral equations approach to internal (two-layer) solitary waves. Phys. Fluids 8, 2032–2047.CrossRefGoogle Scholar
14. Farmer, D. M. 1978 Observations of long nonlinear internal waves in a lake. J. Phys. Oceanogr. 8, 63–73.2.0.CO;2>CrossRefGoogle Scholar
15. Grimshaw, R., Pelinovsky, E. & Ploukhina, O. 2002 Higher-order Korteweg–de Vries models for internal solitary waves in a stratified shear flow with a free surface. Nonlinear Process. Geophys. 9, 221–235.CrossRefGoogle Scholar
16. Grue, J., Friis, H. A., Palm, E. & Rusas, P.-O. 1997 A method for computing unsteady fully nonlinear interfacial waves. J. Fluid Mech. 351, 223–252.CrossRefGoogle Scholar
17. Grue, J., Jensen, A. & Rusas, P.-O. 1999 Properties of large-amplitude internal solitary waves. J. Fluid Mech. 413, 181–217.CrossRefGoogle Scholar
18. Helfrich, K. R. 1992 Internal solitary waves breaking and run-up on a uniform slope. J. Fluid Mech. 243, 133–154.CrossRefGoogle Scholar
19. Hsu, M.-K., Liu, A. K. & Liu, C. 2000 A study of internal waves in the China Seas and Yellow Sea using SAR. Cont. Shelf Res. 20, 389–410.CrossRefGoogle Scholar
20. Huttemann, H. & Hutter, K. 2001 Baroclinic solitary water waves in a two-layered fluid with diffusive interface. Exp. Fluids 30, 317–326.Google Scholar
21. Jo, T.-C. & Choi, W. 2002 Dynamics of strongly nonlinear solitary waves in the shallow water. Stud. Appl. Maths 109, 205–227.CrossRefGoogle Scholar
22. Kao, T. W., Pan, F.-S. & Renouard, D. 1985 Internal soliton on pycnocline: generation, propagation, and shoaling and breaking over slope. J. Fluid Mech. 159, 1965–1985.CrossRefGoogle Scholar
23. Kao, T. W. & Pao, H.-P. 1980 Wave collapse in the thermocline and internal solitary waves. J. Fluid Mech. 97, 116–127.CrossRefGoogle Scholar
24. Lamb, K. G. 2000 Conjugate flows for a three-layer fluid. Phys. Fluids 12 (9), 2169–2185.CrossRefGoogle Scholar
25. Lee, C.-Y. & Beardsley, R. C. 1974 The generation of long nonlinear internal waves in a weakly stratified shear flow. J. Geophys. Res. 79, 453–462.CrossRefGoogle Scholar
26. Liu, A. K. 1988 Analysis of nonlinear internal waves in the New York Bight. J. Geophys. Res. 93, 122–317.CrossRefGoogle Scholar
27. Liu, A. K., Chang, Y. S., Hsu, M.-K. & Liang, N. K. 1998 Evolution of nonlinear internal waves in the East and South China Seas. J. Geophys. Res. 103, 7995–8008.CrossRefGoogle Scholar
28. Liu, P. L.-F. 1994 Model equations for wave propagations from deep to shallow water. Adv. Coast. Ocean Engrg. 1, 125–158.CrossRefGoogle Scholar
29. Lynett, P. & Liu, P. L.-F. 2002 A two-dimensional, depth-integrated model for internal wave propagation over variable bathymetry. Wave Motion 36, 221–240.CrossRefGoogle Scholar
30. Lynett, P., Wu, T.-R. & Liu, P. L.-F. 2002 Modeling wave runup with depth-integrated equations. Coast. Engng 46, 89–107.CrossRefGoogle Scholar
31. Maxworthy, T. 1980 On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions. J. Fluid Mech. 96, 47–64.CrossRefGoogle Scholar
32. Maxworthy, T. 1983 Experiments on solitary internal Kelvin waves. J. Fluid Mech. 129, 365–383.CrossRefGoogle Scholar
33. Mei, C. C. 1989 The Applied Dynamics of Ocean Surface Waves. World Scientific.Google Scholar
34. Michallet, H. & Barthelemy, E. 1998 Experimental study of interfacial solitary waves. J. Fluid Mech. 206, 159–177.CrossRefGoogle Scholar
35. Miyata, M. 1985 An internal solitary wave of large amplitude. La Mer 23, 43–48.Google Scholar
36. Miyata, M. 1988 Long internal waves of large ampliude. In Nonlinear Water Waves, IUTAM Symposium, Tokyo 1987 (ed. Horikawa, K & Maruo, H ), pp. 399–406. Springer.Google Scholar
37. Ostrovsky, L. A. & Grue, J. 2003 Evolution equations for strongly nonlinear internal waves. Phys. Fluids 15, 2934–2948.CrossRefGoogle Scholar
38. Rusas, P.-O. & Grue, J. 2002 Solitary waves and conjugate flows in a three-layer fluid. Eur. J. Mech. B/Fluids 21, 185–206.CrossRefGoogle Scholar
39. Saffarinia, K. & Kao, T. W. 1996 A numerical study of the breaking of internal soliton and its interaction with a slope. Dyn. Atmos. Oceans 23 (1/4), 379–391.CrossRefGoogle Scholar
40. Sandstrom, H. & Elliot, J. A. 1984 Internal tide and solitons on the Scotian shelf: a nutrient pump at work. J. Geophys. Res. 89 (4), 6415–6426.CrossRefGoogle Scholar
41. Small, J. 2001a A nonlinear model of the shoaling and refraction of interfacial solitary waves in the ocean. Part I. Development of the model and investigations of the shoaling effect. J. Phys. Oceanogr. 31, 3163–3183.2.0.CO;2>CrossRefGoogle Scholar
42. Small, J. 2001b A nonlinear model of the shoaling and refraction of interfacial solitary waves in the ocean. Part II. Oblique refraction across a continental slope and propagation over a seamount. J. Phys. Oceanogr. 31, 3184–3199.2.0.CO;2>CrossRefGoogle Scholar
43. Stamp, A. P. & Jacka, M. 1995 Deep-water internal solitary waves. J. Fluid Mech. 305, 347–371.CrossRefGoogle Scholar
44. Stanton, T. P. & Ostrovsky, L. A. 1998 Observations of highly nonlinear solitons over continental shelf. Geophys. Res. Lett. 25, 2695–2698.CrossRefGoogle Scholar
45. Terez, D. E. & Knio, O. M. 1998 Numerical simulations of large-amplitude internal solitary waves. J. Fluid Mech. 362, 53–82.CrossRefGoogle Scholar
46. Tomasson, G. & Melville, W. 1992 Geostrophic adjustment in a channel: nonlinear and dispersive effects. J. Fluid Mech. 241, 23–57.CrossRefGoogle Scholar
47. Turner, R. E. L. & Vanden-Broeck, J.-M. 1988 Broadening of interfacial solitary waves. Phys. Fluids 31, 2486–2491.CrossRefGoogle Scholar
48. Vazquez, A., Stashchuk, N., Vlasenko, V., Bruno, M., Izquierdo, A. & Gallacher, P. C. 2006 Evidence of multimodal structure of the baroclinic tide in the Strait of Gibraltar. Geophys. Res. Lett. 33, L17605.CrossRefGoogle Scholar
49. Vlasenko, V. I. 1994 Multi-modal soliton of internal waves. Atmos. Ocean. Phys. 30, 161–169.Google Scholar
50. Vlasenko, V. I. & Alpers, W. 2005 Generation of secondary internal waves by the interaction of an internal solitary wave with an underwater bank. J. Geophys. Res. 110, C02019.CrossRefGoogle Scholar
51. Vlasenko, V. I. & Hutter, K. 2001 Generation of second mode solitary waves by the interaction of a first model soliton with a sill. Nonlinear Process. Geophys. 8, 223–239.CrossRefGoogle Scholar
52. Wang, X. 2008 Numerical modelling of surface and internal waves over shallow and intermediate water. PhD Thesis, Cornell University.Google Scholar
53. Wei, G. & Kirby, J. T. 1995 A time-dependent numerical code for extended Boussinesq equations. J. Waterways Port Coast. Engrg 121, 251–261.CrossRefGoogle Scholar
54. Yang, Y.-J., Tang, T. Y., Chang, M. H., Liu, A. K., Hsu, M.-K. & Ramp, S. 2004 Solitons northeast of Tung-Sha Island during the ASIAEX pilot studies. IEEE J. Ocean. Engng 29 (4), 1182–1199.CrossRefGoogle Scholar