Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T18:01:57.807Z Has data issue: false hasContentIssue false
  • English
  • Français

A multifractal model for the velocity gradient dynamics in turbulent flows

Published online by Cambridge University Press:  01 February 2018

Rodrigo M. Pereira Open the ORCID record for Rodrigo M. Pereira [Opens in a new window] ,
Luca Moriconi  and
Laurent Chevillard
Rodrigo M. Pereira*
Affiliation:
Laboratório de Física Teórica e Computacional, Departamento de Física, Universidade Federal de Pernambuco, 50670-901, Recife, PE, Brazil
Luca Moriconi
Affiliation:
Instituto de Física, Universidade Federal do Rio de Janeiro, CP 68528, 21945-970, Rio de Janeiro, RJ, Brazil
Laurent Chevillard
Affiliation:
Univ. Lyon, Ens. de Lyon, Univ. Claude Bernard, CNRS, Laboratoire de Physique, 46 allée d’Italie F-69342 Lyon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a stochastic model for the velocity gradient dynamics along a Lagrangian trajectory in isotropic and homogeneous turbulent flows. Comparing with different attempts proposed in the literature, the present model, at the cost of introducing a free parameter known in turbulence phenomenology as the intermittency coefficient, gives a realistic picture of velocity gradient statistics at any Reynolds number. To achieve this level of accuracy, we use as a first modelling step a regularized self-stretching term in the framework of the recent fluid deformation (RFD) approximation that was shown to give a realistic picture of small-scale statistics of turbulence only up to moderate Reynolds numbers. As a second step, we constrain the dynamics, in the spirit of Girimaji & Pope (Phys. Fluids A, vol. 2, 1990, p. 242), in order to impose a peculiar statistical structure to the dissipation seen by the Lagrangian particle. This probabilistic closure uses as a building block a random field that fulfils the statistical description of the intermittency, i.e. multifractal, phenomenon. To do so, we define and generalize to a statistically stationary framework a proposition made by Schmitt (Eur. Phys. J. B, vol. 34, 2003, p. 85). These considerations lead us to propose a nonlinear and non-Markovian closed dynamics for the elements of the velocity gradient tensor. We numerically integrate this dynamics and observe that a stationary regime is indeed reached, in which (i) the gradient variance is proportional to the Reynolds number, (ii) gradients are typically correlated over the (small) Kolmogorov time scale and gradient norms over the (large) integral time scale, (iii) the joint probability distribution function of the two non-vanishing invariants 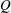$Q$ and 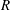$R$ reproduces the characteristic teardrop shape, (iv) vorticity becomes preferentially aligned with the intermediate eigendirection of the deformation tensor and (v) gradients are strongly non-Gaussian and intermittent, a behaviour that we quantify by appropriate high-order moments. Additionally, we examine the problem of rotation rate statistics of (axisymmetric) anisotropic particles as observed in direct numerical simulations. Although our realistic picture of velocity gradient fluctuations leads to better results when compared to the former RFD approximation, it is still unable to provide an accurate description for the rotation rate variance of oblate spheroids.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Intermittency Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 839 , 25 March 2018 , pp. 430 - 467
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afonso, M. M. & Meneveau, C. 2010 Recent fluid deformation closure for velocity gradient tensor dynamics in turbulence: timescale effects and expansions. Physica D 239 (14), 1241–1250.Google Scholar
Antonia, R. A., Phan Thien, N. & Satyaprakash, B. R. 1981 Autocorrelation and spectrum of dissipation fluctuations in a turbulent jet. Phys. Fluids 24, 554–555.Google Scholar
Biferale, L., Chevillard, L., Meneveau, C. & Toschi, F. 2007 Multiscale model of gradient evolution in turbulent flows. Phys. Rev. Lett. 98, 214501.Google Scholar
Borgas, M. S. 1993 The multifractal Lagrangian nature of turbulence. Phil. Trans. R. Soc. Lond. A 342, 379–411.Google Scholar
Cantwell, B. 1992 Exact solution of a restricted Euler equation for the velocity gradient tensor. Phys. Fluids A 4, 782–793.CrossRefGoogle Scholar
Cheridito, P., Kawaguchi, H. & Maejima, M. 2003 Fractional Ornstein–Uhlenbeck processes. Electron. J. Probab. 8 (3), 1–14.CrossRefGoogle Scholar
Chevillard, L., Castaing, B., Arneodo, A., Lévêque, E., Pinton, J.-F. & Roux, S. 2012 A phenomenological theory of Eulerian and Lagrangian velocity fluctuations in turbulent flows. C. R. Physique 13, 899–928.Google Scholar
Chevillard, L., Lévêque, E., Taddia, F., Meneveau, C., Yu, H. & Rosales, C. 2011 Local and nonlocal pressure Hessian effects in real and synthetic fluid turbulence. Phys. Fluids 23, 095108.Google Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97, 174501.Google Scholar
Chevillard, L. & Meneveau, C. 2013 Orientation dynamics of small, triaxial–ellipsoidal particles in isotropic turbulence. J. Fluid Mech. 737, 571–596.Google Scholar
Chevillard, L., Meneveau, C., Biferale, L. & Toschi, F. 2008 Modeling the pressure Hessian and viscous Laplacian in turbulence: comparisons with direct numerical simulation and implications on velocity gradient dynamics. Phys. Fluids 20, 101504.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence, The Legacy of A.N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Gagne, Y. & Hopfinger, E. J. 1979 High order dissipation correlations and structure functions in an axisymmetric jet and a plane channel flow. In Proceedings of the 2nd Symposium on Turbulent Shear Flows, Imperial College, London.Google Scholar
Girimaji, S. S. & Pope, S. B. 1990 A diffusion model for velocity gradients in turbulence. Phys. Fluids A 2, 242–256.Google Scholar
Girimaji, S. S. & Speziale, C. G. 1995 A modified restricted Euler equation for turbulent flows with mean velocity gradients. Phys. Fluids 7 (6), 1438–1446.CrossRefGoogle Scholar
Grigorio, L. S., Bouchet, F., Pereira, R. M. & Chevillard, L. 2017 Instantons in a Lagrangian model of turbulence. J. Phys. A 50 (5), 055501.CrossRefGoogle Scholar
Guala, M., Lüthi, B., Liberzon, A., Tsinober, A. & Kinzelbach, W. 2005 On the evolution of material lines and vorticity in homogeneous turbulence. J. Fluid Mech. 533, 339–359.Google Scholar
Gustavsson, K., Einarsson, J. & Mehlig, B. 2014 Tumbling of small axisymmetric particles in random and turbulent flows. Phys. Rev. Lett. 112, 014501.Google Scholar
Huang, Y. & Schmitt, F. G. 2014 Lagrangian cascade in three-dimensional homogeneous and isotropic turbulence. J. Fluid Mech. 741, R2.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Johnson, P. L. & Meneveau, C. 2016 A closure for Lagrangian velocity gradient evolution in turbulence using recent-deformation mapping of initially Gaussian fields. J. Fluid Mech. 804, 387–419.Google Scholar
Johnson, P. L. & Meneveau, C. 2017 Turbulence intermittency in a multiple-time-scale Navier–Stokes-based reduced model. Phys. Rev. Fluids 2, 072601.Google Scholar
Kahane, J.-P. 1985 Sur le chaos multiplicatif. Ann. Sci. Math. Québec 9, 105–150.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Li, Y., Perlman, E., Wan, M., Yang, Y., Burns, R., Meneveau, C., Burns, R., Chen, S., Szalay, A. & Eyink, G. 2008 A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 9 (31), 1–29.Google Scholar
Mandelbrot, B. B. 1972 Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence. In Lecture Notes in Physics (ed. Rosenblatt, M. & Van Atta, C.), vol. 12, pp. 333–351. Springer.Google Scholar
Mandelbrot, B. B. & Van Ness, J. W. 1968 Fractional Brownian motion, fractional noises and applications. SIAM Rev. 10, 422–437.CrossRefGoogle Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.Google Scholar
Moriconi, L., Pereira, R. M. & Grigorio, L. S. 2014 Velocity-gradient probability distribution functions in a Lagrangian model of turbulence. J. Stat. Mech. 2014, P10015.Google Scholar
Novikov, E. A. 1989 Two particle description of turbulence, markov property, and intermittency. Phys. Fluids A 1 (2), 326–330.Google Scholar
Novikov, E. A. 1990 The effects of intermittency on statistical characteristics of turbulence and scale similarity of breakdown coefficients. Phys. Fluids A 2 (5), 814–820.CrossRefGoogle Scholar
Obukhov, A. M. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13, 77–81.CrossRefGoogle Scholar
Ohkitani, K. 1993 Eigenvalue problems in three-dimensional Euler flows. Phys. Fluids A 5 (10), 2570–2572.Google Scholar
Parsa, S., Calzavarini, E., Toschi, F. & Voth, G. A. 2012 Rotation rate of rods in turbulent fluid flow. Phys. Rev. Lett. 109, 134501.Google Scholar
Pereira, R. M., Garban, C. & Chevillard, L. 2016 A dissipative random velocity field for fully developed fluid turbulence. J. Fluid Mech. 794, 369–408.CrossRefGoogle Scholar
Pope, S. B. 1990 Lagrangian microscales in turbulence. Phil. Trans. R. Soc. Lond. A 333 (1631), 309–319.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pumir, A. & Wilkinson, M. 2011 Orientation statistics of small particles in turbulence. New J. Phys. 13 (9), 093030.Google Scholar
Rhodes, R. & Vargas, V. 2014 Gaussian multiplicative chaos and applications: a review. Prob. Surv. 11, 315–392.Google Scholar
Schmitt, F. G. 2003 A causal multifractal stochastic equation and its statistical properties. Eur. Phys. J. B 34, 85–91.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.Google Scholar
Tsinober, A. 2001 An Informal Introduction to Turbulence. Kluwer Academic.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23 (2), 252–257.Google Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. Phys. (Paris) 43, 837–842.Google Scholar
Voth, G. A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.Google Scholar
Wallace, J. 2009 Twenty years of experimental and direct numerical simulation access to the velocity gradient tensor: what have we learned about turbulence? Phys. Fluids 21, 021301.Google Scholar
Wilczek, M. & Meneveau, C. 2014 Pressure Hessian and viscous contributions to velocity gradient statistics based on Gaussian random fields. J. Fluid Mech. 756, 191–225.Google Scholar
Yaglom, A. M. 1966 Effect of fluctuations in energy dissipation rate on the form of turbulence characteristics in the inertial subrange. Dokl. Akad. Nauk SSSR 166, 49–52.Google Scholar
Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.CrossRefGoogle Scholar
Yu, H. & Meneveau, C. 2010 Lagrangian refined Kolmogorov similarity hypothesis for gradient time evolution and correlation in turbulent flows. Phys. Rev. Lett. 104, 084502.CrossRefGoogle ScholarPubMed