Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-23T03:40:48.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Motion of an oil droplet through a capillary with charged surfaces

Published online by Cambridge University Press:  18 March 2019

P. Grassia Open the ORCID record for P. Grassia [Opens in a new window]
P. Grassia*
Affiliation:
Department of Chemical and Process Engineering, University of Strathclyde, James Weir Building, 75 Montrose St, Glasgow G1 1XJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A model developed by Wilmott et al. (J. Fluid Mech., vol. 841, 2018, pp. 310–350) for the advance of a charged oil droplet along a charged capillary pore is considered. The oil droplet is surrounded by an aqueous phase filling the pore, and the model considers a uniformly curved capillary static droplet front plus an aqueous thin film separating the body of the oil droplet from the capillary wall, with these two regions being joined by a transition region. The methodology follows a classical asymptotic approach proposed by Bretherton (J. Fluid Mech., vol. 10, 1961, pp. 166–188) but incorporates additional electro-osmotic effects (specifically an electro-osmotic disjoining tension) due to the charged surfaces. A number of dimensionless parameters control the model’s behaviour, of which the most important is denoted 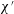$\unicode[STIX]{x1D712}^{\prime }$ and represents the ratio between the ‘nominal’ thickness of the aqueous film (as determined neglecting any electrostatic effects) and the Debye length within the film, which is sensitive to ion concentrations and hence to salinity. When 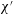$\unicode[STIX]{x1D712}^{\prime }$ is large, electro-osmotic effects are screened and Bretherton’s classical results are recovered. However as 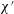$\unicode[STIX]{x1D712}^{\prime }$ decreases, electro-osmotic effects come into play and the film becomes much thicker than Bretherton’s prediction to ensure that screening effects are not altogether lost, and also there is a noticeable increase in the pressure needed to drive the droplet front along. These results apply with minor variations in the case of singly charged surfaces (charge on either oil or on the capillary wall), oil and wall surfaces with like charges, or oil and wall surfaces with opposite but unequal charges. However in the case of opposite and equal charges, the system’s behaviour changes dramatically. There is now a conjoining electro-osmotic pressure rather than a disjoining tension, the film becomes thinner than the analogous Bretherton film, and the pressure needed to drive the droplet front along decreases. Surprisingly in this case, for sufficiently small 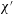$\unicode[STIX]{x1D712}^{\prime }$, the work done by the conjoining pressure can exceed the work done against viscous dissipation, meaning the pressure required to drive the droplet front is not just smaller than in Bretherton’s predictions but also slightly less than would be estimated based on capillary forces alone. Although the main effect of reducing salinity is to increase Debye length and hence reduce 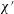$\unicode[STIX]{x1D712}^{\prime }$, salinity also affects surface charges. A situation is explored whereby reducing salinity affects charges, producing a switch from disjoining tensions to conjoining pressures and back again: this leads to a non-monotonic response in film thickness and pressure required to drive the droplet front along.

JFM classification

Drops and Bubbles: Drops Interfacial Flows (free surface): Capillary flows Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 721 - 758
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austad, T., RezaeiDoust, A. & Puntervold, T. 2010 Chemical mechanism of low salinity water flooding in sandstone reservoirs. In SPE Improved Oil Recovery Symposium, Tulsa, OK, 24th–28th Apr, Society of Petroleum Engineers.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10, 166–188.10.1017/S0022112061000160Google Scholar
Buckley, J. S.1996 Mechanisms and consequences of wettability alteration by crude oils. PhD thesis, Heriot-Watt University.Google Scholar
Burgess, D. & Foster, M. R. 1990 Analysis of the boundary conditions for a Hele-Shaw bubble. Phys. Fluids A 2, 1105–1117.10.1063/1.857610Google Scholar
Cantat, I. 2013 Liquid meniscus friction on a wet plate: bubbles, lamellae and foams. Phys. Fluids 25, 031303.Google Scholar
Cantat, I., Kern, N. & Delannay, R. 2004 Dissipation in foam flowing through narrow channels. Europhys. Lett. 65, 726–732.Google Scholar
Cobos, S., Carvalho, M. S. & Alvarado, V. 2009 Flow of oil–water emulsions through a constricted capillary. Intl J. Multiphase Flow 35, 507–515.10.1016/j.ijmultiphaseflow.2009.02.018Google Scholar
Cox, S. J., Kraynik, A. M., Weaire, D. & Hutzler, S. 2018 Ideal wet two-dimensional foams and emulsions with finite contact angle. Soft Matt. 14, 5922–5929.10.1039/C8SM00739JGoogle Scholar
Fletcher, P. & Sposito, G. 1989 Chemical modeling of clay/electrolyte interactions of montmorillonite. Clay Miner. 24, 375–391.10.1180/claymin.1989.024.2.14Google Scholar
Fournier, P., Oelkers, E. H., Gout, R. & Pokrovski, G. 1998 Experimental determination of aqueous sodium-acetate dissociation constants at temperatures from 20 to 240 °C. Chem. Geol. 151, 69–84.10.1016/S0009-2541(98)00071-0Google Scholar
Gauri, V. & Koelling, K. W. 1999 The motion of long bubbles through viscoelastic fluids in capillary tubes. Rheol. Acta 38, 458–470.10.1007/s003970050197Google Scholar
Giavedoni, M. D. & Saita, F. A. 1997 The axisymmetric and plane cases of a gas phase steadily displacing a Newtonian liquid: a simultaneous solution of the governing equations. Phys. Fluids 9, 2420–2428.Google Scholar
Giavedoni, M. D. & Saita, F. A. 1999 The rear meniscus of a long bubble steadily displacing a Newtonian liquid in a capillary tube. Phys. Fluids 11, 786–794.Google Scholar
Green, T. E., Bramley, A., Lue, L. & Grassia, P. 2006 Viscous froth lens. Phys. Rev. E 74, 051403.Google Scholar
Hazel, A. L. & Heil, M. 2002 The steady propagation of a semi infinite bubble into a tube of elliptical or rectangular cross-section. J. Fluid Mech. 470, 91–114.Google Scholar
Heil, M. 2001 Finite Reynolds number effects in the Bretherton problem. Phys. Fluids 13, 2517–2521.10.1063/1.1389861Google Scholar
Joseph, N. R. 1946 The dissociation constants of organic calcium complexes. J. Biol. Chem. 164, 529–541.Google Scholar
Krechetnikov, R. & Homsy, G. M. 2005 Dip coating in the presence of a substrate-liquid interaction potential. Phys. Fluids 17, 102105.Google Scholar
Laborie, B., Rouyer, F., Angelescu, D. E. & Lorenceau, E. 2017 Yield-stress fluid deposition in circular channels. J. Fluid Mech. 818, 838–851.10.1017/jfm.2017.161Google Scholar
Lager, A., Webb, K., Black, C., Singleton, M. & Sorbie, K. 2008 Low salinity oil recovery: an experimental investigation. Petrophys. 49, 28–35.Google Scholar
Lee, S., Webb, K., Collins, I., Lager, A., Clarke, S., O’Sullivan, M., Routh, A. & Wang, X. 2010 Low salinity oil recovery: increasing understanding of the underlying mechanisms. In SPE Improved Oil Recovery Symposium, Tulsa, OK, 24th–28th April, Society of Petroleum Engineers.Google Scholar
Lewis, W. C. M. 1937 The electric charge at an oil–water interface. Trans. Faraday Soc. 33, 708–713.Google Scholar
Li, S. & Xu, R. 2008 Electrical double layers interaction between oppositely charged particles as related to surface charge density and ionic strength. Colloids Surf. A 326, 157–161.10.1016/j.colsurfa.2008.05.023Google Scholar
Ligthelm, D. J., Gronsveld, J., Hofman, J., Brussee, N., Marcelis, F. & van der Linde, H. 2009 Novel waterflooding strategy by manipulation of injection brine composition. In EUROPEC/EAGE Conference and Exhibition, Amsterdam, Netherlands, 8th–11th June.Google Scholar
Malmberg, C. G. & Maryott, A. A. 1956 Dielectric constant of water from 0° to 100 °C. J. Res. Natl Bur. Stand. 56, 1–8.Google Scholar
McGuire, P. L., Chatham, J. R., Paskvan, F. K., Sommer, D. M. & Carini, F. H. 2005 Low salinity oil recovery: an exciting new EOR opportunity for Alaska’s north slope. In SPE Western Regional Meeting, Irvine, CA, 30th March–1st April.Google Scholar
Nelson, P. 2009 Pore-throat sizes in sandstones, tight sandstones, and shales. AAPG Bull. 93, 329–340.10.1306/10240808059Google Scholar
Newcombe, G. & Ralston, J. 1992 Wetting dynamics studies on silica surfaces of varied hydrophobicity. Langmuir 8, 190–196.Google Scholar
Park, C. W. & Homsy, G. M. 1984 Two-phase displacement in Hele Shaw cells: theory. J. Fluid Mech. 139, 291–308.10.1017/S0022112084000367Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 1992 Numerical Recipes in C: The Art of Scientific Computing, 2nd edn. Cambridge University Press.Google Scholar
Reif, F. 1965 Fundamentals of Statistical and Thermal Physics. McGraw-Hill.Google Scholar
Reinelt, D. A. & Kraynik, A. M. 1990 On the shearing flow of foams and concentrated emulsions. J. Fluid Mech. 215, 431–455.Google Scholar
RezaeiDoust, A., Puntervold, T. & Austad, T. 2011 Chemical verification of the EOR mechanism by using low saline/smart water in sandstone. Energy Fuels 25, 2151–2162.10.1021/ef200215yGoogle Scholar
Ro, J. S. & Homsy, G. M. 1995 Viscoelastic free-surface flows: thin-film hydrodynamics of Hele-Shaw and dip coating flows. J. Non-Newtonian Fluid Mech. 57, 203–225.Google Scholar
Saugey, A., Drenckhan, W. & Weaire, D. 2006 Wall slip of bubbles in foams. Phys. Fluids 18, 053101.Google Scholar
Severino, M., Giavedoni, M. D. & Saita, F. A. 2003 A gas phase displacing a liquid with soluble surfactants out of a small conduit: the plane case. Phys. Fluids 15, 2961–2972.10.1063/1.1605424Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1987 How liquids spread on solids. Chem. Engng Commun. 55, 41–82.10.1080/00986448708911919Google Scholar
Teletzke, G. F., Davis, H. T. & Scriven, L. E. 1988 Wetting hydrodynamics. Revue Phys. Appl. 23, 989–1007.Google Scholar
Ubal, S., Campana, D. M., Giavedoni, M. D. & Saita, F. A. 2008 Stability of the steady-state displacement of a liquid plug driven by a constant pressure difference along a prewetted capillary tube. Ind. Engng Chem. Res. 47, 6307–6315.10.1021/ie8000309Google Scholar
Vancauwenberghe, V., Di Marco, P. & Brutin, D. 2013 Wetting and evaporation of a sessile drop under an external electrical field: a review. Colloids Surf. A 432, 50–56.Google Scholar
Waghmare, P. R. & Mitra, S. K. 2008 Investigation of combined electro-osmotic and pressure-driven flow in rough microchannels. Trans. ASME J. Fluids Engng 130, 061204.Google Scholar
Willhite, G. P. 1986 Waterflooding. Society of Petroleum Engineers.Google Scholar
Wilmott, Z. M., Breward, C. J. & Chapman, S. J. 2018 The effect of ions on the motion of an oil slug through a charged capillary. J. Fluid Mech. 841, 310–350.Google Scholar
Wong, H., Radke, C. J. & Morris, S. 1995a The motion of long bubbles in polygonal capillaries. 1. Thin films. J. Fluid Mech. 292, 71–94.Google Scholar
Wong, H., Radke, C. J. & Morris, S. 1995b The motion of long bubbles in polygonal capillaries. 2. Drag, fluid pressure and fluid flow. J. Fluid Mech. 292, 95–110.Google Scholar
Wright, M. R. 2007 An Introduction to Aqueous Electrolyte Solutions. Wiley.Google Scholar
Xiao, L., Cai, Q., Ye, X., Wang, J. & Luo, R. 2013 Electrostatic forces in the Poisson-Boltzmann systems. J. Chem. Phys. 139, 094106.Google Scholar
Yang, R.-J., Fu, L.-M. & Hwang, C.-C. 2001 Electroosmotic entry flow in a microchannel. J. Colloid Interface Sci. 244, 173–179.Google Scholar
Yildiz, H. & Morrow, N. 1996 Effect of brine composition on recovery of Moutray crude oil by waterflooding. J. Petrol. Sci. Engng 14, 159–168.Google Scholar