Article contents
Morphodynamics of active nematic fluid surfaces
Published online by Cambridge University Press: 10 February 2023
Abstract
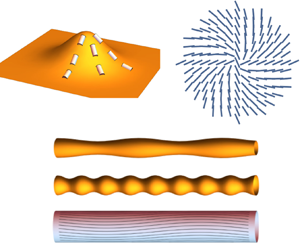
Morphodynamic equations governing the behaviour of active nematic fluids on deformable curved surfaces are constructed in the large deformation limit. Emphasis is placed on the formulation of objective rates that account for normal deformations whilst ensuring that tangential flows are Eulerian, and the use of the surface derivative (rather than the covariant derivative) in the nematic free energy, which elastically couples local order to out-of-plane bending of the surface. Focusing on surface geometry and its dynamical interplay with the hydrodynamics, several illustrative instabilities are then characterised. These include cases where the role of the Scriven–Love number and its nematic analogue are non-negligible, and where the active nematic forcing can be characterised by an analogue of the Föppl–von Kármán number. For the former, flows and changes to the nematic texture are coupled to surface geometry by viscous dissipation. This is shown to result in non-trivial relaxation dynamics for a nematic tube. For the latter, the nematic active forcing couples to the surface bending terms of the nematic free energy, resulting in extensile (active ruffling) and contractile (active pearling) instabilities in the tube shape, as well as active bend instabilities in the nematic texture. In comparison to the flat case, such bend instabilities now have a threshold set by the extrinsic curvature of the tube. Finally, we examine a topological defect located on an almost flat surface, and show that there exists a steady state where a combination of defect elasticity, activity and non-negligible spin connection drive a shape change in the surface.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 13
- Cited by



