Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-07T10:32:36.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Moffatt vortices induced by the motion of a contact line

Published online by Cambridge University Press:  04 April 2014

E. Kirkinis  and
S. H. Davis
E. Kirkinis*
Affiliation:
Department of Engineering Sciences and Applied Mathematics, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208-3125, USA School of Mathematical Sciences, Queensland University of Technology, GPO Box 2434, Brisbane, Queensland 4001, Australia
S. H. Davis
Affiliation:
Department of Engineering Sciences and Applied Mathematics, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208-3125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A recent hydrodynamic theory of liquid slippage on a solid substrate (Kirkinis & Davis, Phys. Rev. Lett., vol. 110, 2013, 234503) gives rise to a sequence of eddies (Moffatt vortices) that co-move with a moving contact line (CL) in a liquid wedge. The presence of these vortices is established through secular equations that depend on the dynamic contact angle $\alpha $ and capillary number Ca. The limiting case 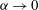$\alpha \rightarrow 0$ is associated with the appearance of such vortices in a channel. The vortices are generated by the relative motion of the interfaces, which in turn is due to the motion of the CL. This effect has yet to be observed in experiment.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Thin films
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 746 , 10 May 2014 , R3
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D. M. & Davis, S. H. 1993 Two-fluid viscous flow in a corner. J. Fluid Mech. 257, 1–31.Google Scholar
Brochard-Wyart, F. & de Gennes, P. G. 1992 Dynamics of partial wetting. Adv. Colloid Interface Sci. 39, 1–11.Google Scholar
Davis, A. M. J. & O’Neill, M. E. 1977 Separation in a Stokes flow past a plane with a cylindrical ridge or trough. Q. J. Mech. Appl. Maths 30 (4), 355–368.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.Google Scholar
de Gennes, P. G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves. Springer.Google Scholar
Hoffman, R. L. 1975 A study of the advancing interface. I. Interface shape in liquid–gas systems. J. Colloid Interface Sci. 50 (2), 228–241.Google Scholar
Kirkinis, E. & Davis, S. H. 2013 Hydrodynamic theory of liquid slippage on a solid substrate near a moving contact line. Phys. Rev. Lett. 110, 234503.Google Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18 (1), 1–18.Google Scholar
Moffatt, H. K. & Duffy, B. R. 1980 Local similarity solutions and their limitations. J. Fluid Mech. 96 (02), 299–313.Google Scholar
Pan, F. & Acrivos, A. 1967 Steady flows in rectangular cavities. J. Fluid Mech. 28 (4), 643–655.Google Scholar
Taneda, S. 1979 Visualization of separating Stokes flows. J. Phys. Soc. Japan 46 (6), 1935–1942.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. D: Appl. Phys. 12 (9), 1473–1484.Google Scholar