Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T04:25:03.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling falling film flow: an adjustable formulation

Published online by Cambridge University Press:  29 November 2022

Sanghasri Mukhopadhyay Open the ORCID record for Sanghasri Mukhopadhyay [Opens in a new window] ,
Christian Ruyer-Quil Open the ORCID record for Christian Ruyer-Quil [Opens in a new window]  and
R. Usha Open the ORCID record for R. Usha [Opens in a new window]
Sanghasri Mukhopadhyay
Affiliation:
Department of Mathematics, School of Advanced Science, Vellore Institute of Technology, Vellore 632014, Tamil Nadu, India
Christian Ruyer-Quil*
Affiliation:
Université Savoie Mont Blanc, CNRS, LOCIE, 73000 Chambéry, France
R. Usha
Affiliation:
Department of Mathematics, IIT Madras, Chennai 600036, Tamil Nadu, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

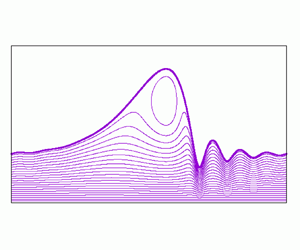
A new two-equation model for gravity-driven liquid film flow based on the long-wave expansion has been derived. The novelty of the model consists in using a base velocity profile combining parabolic (Ruyer-Quil & Manneville, Eur. Phys. J. B, vol. 15, issue 2, 2000, pp. 357–369) and ellipse (Usha et al., Phys. Fluids, vol. 32, issue 1, 2020, 013603) profile functions in the wall-normal coordinate. The dependence on a free parameter $A$ related to the eccentricity of an ellipse serves as an adjustable parameter. The resulting models are consistent at $O(\varepsilon )$ for inertia terms and at $O(\varepsilon ^2)$ for viscous diffusion effects, and predict accurately the primary instability. Appropriate tuning of the adjustable parameter helps to recover accurate predictions for the asymptotic wave celerity of nonlinear solitary waves. Further, the model is shown to capture the closed separation vortices that can form underneath the troughs of precursory capillary ripples.

JFM classification

Interfacial Flows (free surface): Thin films Nonlinear Dynamical Systems: Low-dimensional models Waves/Free-surface Flows: Solitary waves
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , R3
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Cellier, N. & Ruyer-Quil, C. 2020 A new family of reduced models for non-isothermal falling films. Intl J. Heat Mass Transfer 154, 119700.CrossRefGoogle Scholar
Chakraborty, S., Nguyen, P.-K., Ruyer-Quil, C. & Bontozoglou, V. 2014 Extreme solitary waves on falling liquid films. J. Fluid Mech. 745, 564–591.CrossRefGoogle Scholar
Dietze, G.F., Al-Sibai, F. & Kneer, R. 2009 Experimental study of flow separation in laminar falling liquid films. J. Fluid Mech. 637, 73–104.CrossRefGoogle Scholar
Doedel, E.J., Champneys, A.R., Fairgrieve, T.F., Kuznetsov, Y.A., Sandstede, B. & Wang, X. 2007 AUTO-07p: Continuation and Bifurcation Software for Ordinary Differential Equations (with HomCont). Available at https://sourceforge.net/projects/auto-07p/.Google Scholar
Gerbeau, J.-F. & Perthame, B. 2001 Derivation of viscous Saint-Venant system for laminar shallow water; numerical validation. Discrete Continuous Dyn. Syst. B 1 (1), 89–102.CrossRefGoogle Scholar
Han, Y. & Rogers, R.J. 1996 Squeeze film force modeling for large amplitude motion using an elliptical velocity profile. J. Tribol. 118 (3), 687–692.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M.G. 2012 Falling Liquid Films. Applied Mathematical Sciences, vol. 176. Springer.CrossRefGoogle Scholar
Noble, P. & Vila, J.P. 2013 Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations. J. Fluid Mech. 735, 29–60.CrossRefGoogle Scholar
Ooshida, T. 1999 Surface equation of falling film flows which is valid even far beyond the criticality. Phys. Fluids 11, 3247–3269.Google Scholar
Richard, G.L., Gisclon, M., Ruyer-Quil, C. & Vila, J.P. 2019 Optimization of consistent two-equation models for thin film flows. Eur. J. Mech. B/Fluids 76, 7–25.CrossRefGoogle Scholar
Richard, G.L., Ruyer-Quil, C. & Vila, J.P. 2016 A three-equation model for thin films down an inclined plane. J. Fluid Mech. 804, 162–200.CrossRefGoogle Scholar
Ruyer-Quil, C., Chakraborty, S. & Dandapat, B.S. 2012 Wavy regime of a power-law film flow. J. Fluid Mech. 692, 220–256.CrossRefGoogle Scholar
Ruyer-Quil, C. & Kalliadasis, S. 2012 Wavy regimes of film flow down a fiber. Phys. Rev. E 85, 046302.CrossRefGoogle ScholarPubMed
Ruyer-Quil, C., Kofman, N., Chasseur, D. & Mergui, S. 2014 Dynamics of falling liquid films. Eur. Phys. J. E 37 (4), 30.CrossRefGoogle ScholarPubMed
Ruyer-Quil, C. & Manneville, P. 2000 Improved modeling of flows down inclined planes. Eur. Phys. J. B 15 (2), 357–369.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2002 Further accuracy and convergence results on the modeling of flows down inclined planes by weighted-residual approximations. Phys. Fluids 14 (1), 170–183.CrossRefGoogle Scholar
Ruyer-Quil, C. & Manneville, P. 2005 On the speed of solitary waves running down a vertical wall. J. Fluid Mech. 531, 181–190.CrossRefGoogle Scholar
Samanta, A., Goyeau, B. & Ruyer-Quil, C. 2013 A falling film on a porous medium. J. Fluid Mech. 716, 414–444.CrossRefGoogle Scholar
Usha, R., Chattopadhyay, G. & Tiwari, N. 2020 Evolution of a thin film down an incline: a new perspective. Phys. Fluids 32 (1), 013603.Google Scholar