Published online by Cambridge University Press: 01 October 2020
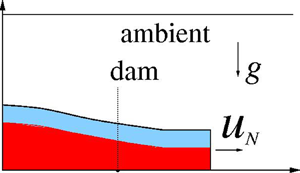
Consider the propagation of a gravity current (GC) released from a lock of length  $x_0$ and height
$x_0$ and height  $h_0$ into an ambient fluid of height
$h_0$ into an ambient fluid of height  $H h_0$ and density
$H h_0$ and density  $\rho _{o}$. The lock contains a layer of thickness
$\rho _{o}$. The lock contains a layer of thickness  $H_L h_0$ of density
$H_L h_0$ of density  $\rho _L$ overlaid by a layer of thickness
$\rho _L$ overlaid by a layer of thickness  $(1-H_L)h_0$ and density
$(1-H_L)h_0$ and density  $\rho _U$, where
$\rho _U$, where  $\rho _{o} < \rho _U < \rho _L$ and
$\rho _{o} < \rho _U < \rho _L$ and  $H_L \in (0, 1)$. Assume Boussinesq and large Reynolds-number flow. The internal stratification parameter is
$H_L \in (0, 1)$. Assume Boussinesq and large Reynolds-number flow. The internal stratification parameter is  $\sigma = (\rho _L - \rho _U)/(\rho _L - \rho _{o})$, in the range
$\sigma = (\rho _L - \rho _U)/(\rho _L - \rho _{o})$, in the range  $(0,1)$; the classical GC is
$(0,1)$; the classical GC is  $\sigma =0$. Such GCs were investigated experimentally (Gladstone et al., Sedimentology, vol. 51, 2004, pp. 767–789; Dai, Phys. Rev. Fluids, vol. 2, 2017, 073802; Wu & Dai, J. Hydraul. Res., 2019, pp. 1–14.); we present a new self-contained model for the prediction of the thickness
$\sigma =0$. Such GCs were investigated experimentally (Gladstone et al., Sedimentology, vol. 51, 2004, pp. 767–789; Dai, Phys. Rev. Fluids, vol. 2, 2017, 073802; Wu & Dai, J. Hydraul. Res., 2019, pp. 1–14.); we present a new self-contained model for the prediction of the thickness  $h$ and depth-averaged velocity
$h$ and depth-averaged velocity  $u$ as functions of distance
$u$ as functions of distance  $x$ and time
$x$ and time  $t$; the position and speed of the nose
$t$; the position and speed of the nose  $x_N(t)$ and
$x_N(t)$ and  $u_N(t)$ follow. We derive a compact scaling upon which, for a given
$u_N(t)$ follow. We derive a compact scaling upon which, for a given  $H$ (height ratio of ambient to lock), the flows differ in only one parameter:
$H$ (height ratio of ambient to lock), the flows differ in only one parameter:  $\varPsi = \{ [1 -\sigma (1 - H_L)]/[1 - \sigma (1 - H_L^2)] \} ^{1/2}$. The parameter
$\varPsi = \{ [1 -\sigma (1 - H_L)]/[1 - \sigma (1 - H_L^2)] \} ^{1/2}$. The parameter  $\varPsi$ equals
$\varPsi$ equals  $1$ for the classical GC and is larger in the presence of stratification; a larger
$1$ for the classical GC and is larger in the presence of stratification; a larger  $\varPsi$ means a faster and a thinner GC. The solution reveals an initial slumping phase with constant
$\varPsi$ means a faster and a thinner GC. The solution reveals an initial slumping phase with constant  $u_N$, a self-similar phase
$u_N$, a self-similar phase  $x_N \sim t^{2/3}$, and the transition at
$x_N \sim t^{2/3}$, and the transition at  $x_V$ to the viscous regime. Comparisons with published experiments show good data collapse with the present scaling
$x_V$ to the viscous regime. Comparisons with published experiments show good data collapse with the present scaling  $\varPsi$, and fair-to-good quantitative agreement (the discrepancy and the stability conditions are discussed).
$\varPsi$, and fair-to-good quantitative agreement (the discrepancy and the stability conditions are discussed).