Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T00:42:23.709Z Has data issue: false hasContentIssue false
  • English
  • Français

The mode B structure of streamwise vortices in the wake of a two-dimensional blunt trailing edge

Published online by Cambridge University Press:  05 December 2019

Bradley Gibeau  and
Sina Ghaemi Open the ORCID record for Sina Ghaemi [Opens in a new window]
Bradley Gibeau
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2R3, Canada
Sina Ghaemi*
Affiliation:
Department of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 2R3, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

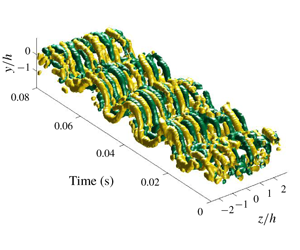
The structure of streamwise vortices that arise due to secondary instabilities in the wake of a two-dimensional blunt body with a chord-to-thickness ratio of 12.5 was investigated using high-speed stereoscopic particle image velocimetry. Reynolds numbers spanning an order of magnitude from $Re(h)=2600$ to 25 800 were considered, where $h$ is the height of the blunt trailing edge. A modified two-dimensional $Q$-criterion ($Q^{\prime }=\unicode[STIX]{x1D714}_{x}Q/|\unicode[STIX]{x1D714}_{x}|$) was applied to identify the streamwise vortices. The wavelength of the streamwise vortices, defined as the spanwise distance between adjacent streamwise vortex pairs in the wake, was investigated by applying an autocorrelation algorithm to snapshots of $Q^{\prime }$. The most probable wavelength was found to range from $0.67h$ to $0.85h$ with increasing $Re$, and the mean wavelengths increased from $0.77h$ to $0.96h$. These wavelength values appeared to increase asymptotically. Visual inspection and cross-correlation analyses based on $Q^{\prime }$ showed that the streamwise vortices maintain their directions of rotation during primary shedding cycles. The latter analysis was carried out at low $Re$ because of a large amount of wake distortion and the absence of time-resolved data at high $Re$. The characteristics of the streamwise vortex structure found here match those of mode B, which, at similar $Re$, dominates the wakes of circular and square cylinders and has also recently been shown to exist in the wake of an elongated blunt body with a larger chord-to-thickness ratio of 46.5 (Gibeau et al., J. Fluid Mech., vol. 846, 2018, pp. 578–604).

JFM classification

Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A12
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, J. P., Mayda, E. A. & van Dam, C. P. 2006 Experimental analysis of thick blunt trailing-edge wind turbine airfoils. J. Solar Energy Engng 128 (4), 422–431.CrossRefGoogle Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bays-Muchmore, B. & Ahmed, A. 1993 On streamwise vortices in turbulent wakes of cylinders. Phys. Fluids A 5 (2), 387–392.CrossRefGoogle Scholar
Berger, E. & Wille, R. 1972 Periodic flow phenomena. Annu. Rev. Fluid Mech. 4, 313–340.CrossRefGoogle Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15 (8), L57.CrossRefGoogle Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Brede, M., Eckelmann, H. & Rockwell, D. 1996 On secondary vortices in the cylinder wake. Phys. Fluids 8 (8), 2117–2124.CrossRefGoogle Scholar
Gerrard, J. H. 1978 The wakes of cylindrical bluff bodies at low Reynolds number. Phil. Trans. R. Soc. Lond. A 288 (1354), 351–382.CrossRefGoogle Scholar
Ghaemi, S., Ragni, D. & Scarano, F. 2012 PIV-based pressure fluctuations in the turbulent boundary layer. Exp. Fluids 53 (6), 1823–1840.CrossRefGoogle Scholar
Gibeau, B., Koch, C. R. & Ghaemi, S. 2018 Secondary instabilities in the wake of an elongated two-dimensional body with a blunt trailing edge. J. Fluid Mech. 846, 578–604.CrossRefGoogle Scholar
Gibeau, B., Koch, C. R. & Ghaemi, S. 2019 Active control of vortex shedding from a blunt trailing edge using oscillating piezoelectric flaps. Phys. Rev. Fluids 4, 054704.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jethani, Y., Kumar, K., Sameen, A. & Mathur, M. 2018 Local origin of mode-B secondary instability in the flow past a circular cylinder. Phys. Rev. Fluids 3, 103902.CrossRefGoogle Scholar
Johnson, M. R. & Kostiuk, L. W. 2000 Efficiencies of low-momentum jet diffusion flames in crosswinds. Combust. Flame 123 (1), 189–200.CrossRefGoogle Scholar
Luo, S. C., Tong, X. H. & Khoo, B. C. 2007 Transition phenomena in the wake of a square cylinder. J. Fluids Struct. 23 (2), 227–248.CrossRefGoogle Scholar
Mansy, H., Yang, P. M. & Williams, D. R. 1994 Quantitative measurements of three-dimensional structures in the wake of a circular cylinder. J. Fluid Mech. 270, 277–296.CrossRefGoogle Scholar
Meinhart, C. D., Wereley, S. T. & Santiago, J. G. 2000 A PIV algorithm for estimating time-averaged velocity fields. J. Fluids Engng 122 (2), 285–289.CrossRefGoogle Scholar
Naghib-Lahouti, A., Doddipatla, L. S. & Hangan, H. 2012 Secondary wake instabilities of a blunt trailing edge profiled body as a basis for flow control. Exp. Fluids 52 (6), 1547–1566.CrossRefGoogle Scholar
Naghib-Lahouti, A., Lavoie, P. & Hangan, H. 2014 Wake instabilities of a blunt trailing edge profiled body at intermediate Reynolds numbers. Exp. Fluids 55 (7), 1779.CrossRefGoogle Scholar
Ng, Z. Y., Vo, T. & Sheard, G. J. 2018 Stability of the wakes of cylinders with triangular cross-sections. J. Fluid Mech. 844, 721–745.CrossRefGoogle Scholar
Oertel, H. 1990 Wakes behind blunt bodies. Annu. Rev. Fluid Mech. 22, 539–564.CrossRefGoogle Scholar
Petrusma, M. S. & Gai, S. L. 1996 Bluff body wakes with free, fixed, and discontinuous separation at low Reynolds numbers and low aspect ratio. Exp. Fluids 20 (3), 189–198.CrossRefGoogle Scholar
Raffel, M., Willert, C. E., Scarano, F., Kähler, C. E. C., Wereley, S. T. & Kompenhans, J. 2018 Particle Image Velocimetry: A Practical Guide. Springer.CrossRefGoogle Scholar
Robichaux, J., Balachandar, S. & Vanka, S. P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.CrossRefGoogle Scholar
Roshko, A. 1954 On the development of turbulent wakes from vortex streets. NACA Rep. 1191.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Scarano, F. & Poelma, C. 2009 Three-dimensional vorticity patterns of cylinder wakes. Exp. Fluids 47 (1), 69–83.CrossRefGoogle Scholar
Sciacchitano, A. & Wieneke, B. 2016 PIV uncertainty propagation. Meas. Sci. Technol. 27, 084006.CrossRefGoogle Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Standish, K. J. & van Dam, C. P. 2003 Aerodynamic analysis of blunt trailing edge airfoils. J. Solar Energy Engng 125 (4), 479–487.CrossRefGoogle Scholar
Tadikamalla, P. R. 1980 A look at the Burr and related distributions. Intl Stat. Rev. 48 (3), 337–344.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15 (3), 607–616.CrossRefGoogle Scholar
Tong, X. H., Luo, S. C. & Khoo, B. C. 2008 Transition phenomena in the wake of an inclined square cylinder. J. Fluids Struct. 24, 994–1005.CrossRefGoogle Scholar
Wei, T. & Smith, C. R. 1986 Secondary vortices in the wake of circular cylinders. J. Fluid Mech. 169, 513–533.CrossRefGoogle Scholar
Westerweel, J. & Scarano, F. 2005 Universal outlier detection for PIV data. Exp. Fluids 39 (6), 1096–1110.CrossRefGoogle Scholar
Wieneke, B. 2005 Stereo-PIV using self-calibration on particle images. Exp. Fluids 39 (2), 267–280.CrossRefGoogle Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31 (11), 3165–3168.CrossRefGoogle Scholar
Williamson, C. H. K. 1989 Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 206, 579–627.CrossRefGoogle Scholar
Williamson, C. H. K. 1992 The natural and forced formation of spot-like ‘vortex dislocations’ in the transition of a wake. J. Fluid Mech. 243, 393–441.CrossRefGoogle Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.CrossRefGoogle Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996 Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 201–222.CrossRefGoogle Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013 Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.CrossRefGoogle Scholar
Yoon, D. H., Yang, K. S. & Choi, C. B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22, 043603.CrossRefGoogle Scholar
Zhang, H. Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.CrossRefGoogle Scholar