Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T11:24:53.016Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing in continuous gravity currents

Published online by Cambridge University Press:  06 April 2017

Diana Sher  and
Andrew W. Woods Open the ORCID record for Andrew W. Woods [Opens in a new window]
Diana Sher
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
Andrew W. Woods*
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present measurements of the entrainment of ambient fluid into high-Reynolds-number gravity currents produced by a steady flux of buoyancy. The currents propagate along a horizontal channel and the mixing is measured using a light attenuation technique to obtain the cross-channel average of the density throughout the current. 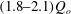The total volume of the current increases linearly with time, at a rate in the range $(1.8{-}2.1)Q_{o}$ for source Froude numbers, 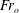$Fr_{o}$, in the range 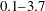$0.1{-}3.7$, where 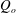$Q_{o}$ is the source volume flux per unit width. Most mixing occurs either immediately downstream of the inflow or near the head of the flow, with an increasing proportion of the entrainment occurring in a mixing zone near the inflow as 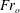$Fr_{o}$ increases. A vertical gradient in the density and horizontal velocity develops in this mixing zone. This enables relatively dense fluid at the base of the current to catch up with the head, where it rises and mixes with the ambient fluid which is displaced over the head. The mixed fluid continues forward more slowly than the head, forming the relatively dilute fluid in the upper part of the current. Our data show that the depth and the depth-averaged buoyancy are primarily dependent on the position relative to the front, with the speed of the front being 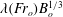$\unicode[STIX]{x1D706}(Fr_{o})B_{o}^{1/3}$, where 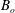$B_{o}$ is the source buoyancy flux per unit width. Here, 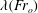$\unicode[STIX]{x1D706}(Fr_{o})$ increases from 0.9 to 1.1 as 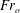$Fr_{o}$ increases from 0.1 to 3.7, while the Froude number at the head of the flow has a value of 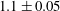$1.1\pm 0.05$.

JFM classification

Geophysical and Geological Flows: Gravity currents Mixing: Mixing
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , R4
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonnecaze, R. T., Huppert, H. E. & Lister, J. R. 1993 Particle-driven gravity currents. J. Fluid Mech. 250, 339–369.Google Scholar
Britter, R. E. 1979 The spread of a negatively buoyant plume in a calm environment. Atmos. Environ. 13, 1241–1247.Google Scholar
Britter, R. E. & Linden, P. F. 1980 The motion of the front of a gravity current travelling down an incline. J. Fluid Mech. 99, 531–543.Google Scholar
Bursik, M. & Woods, A. W. 1996 The dynamics and thermodynamics of large ash flows. Bull. Volcanol. 58, 175–193.CrossRefGoogle Scholar
Cafiero, G. & Woods, A. W. W. 2016 Experiments on mixing in wakes in shallow water. J. Fluid Mech. 804, 351–369.CrossRefGoogle Scholar
Cenedese, C. & Dalziel, S. 1998 Concentration and depth fields determined by the light transmitted through a dyed solution. In Proceedings of the 8th International Symposium on Flow Visualization (ed. Carlomango, G. M. & Grant, I.). ISBN 0953399109.Google Scholar
Chen, J. C. 1980 Studies on Gravitational Spreading Currents. Caltech.Google Scholar
Chowdhury, M. R. & Testik, F. Y. 2014 A review of gravity currents formed by submerged singleport discharges in inland and coastal waters. Environ. Fluid Mech. 14, 265–293.Google Scholar
Chowdhury, M. R. & Testik, F. Y. 2015 Axisymmetric underflows from impinging buoyant jets of dense cohesive particle-laden fluids. J. Hydraul. Engng 141‐3, 1–10.Google Scholar
Dallimore, C. J., Imberger, J. & Ishikawa, T. 2001 Entrainment and turbulence in saline under flow in Lake Ogawara. J. Hydraul. Engng 127‐11, 937–948.CrossRefGoogle Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.Google Scholar
Gratton, J. & Vigo, C. 1994 Self-similar gravity currents with variable inflow revisited: plane currents. J. Fluid Mech. 258, 77–104.Google Scholar
Grundy, R. & Rottman, J. 1986 Self similar solutions of the shallow water equations representing gravity currents with variable inflow. J. Fluid Mech. 169, 337–351.CrossRefGoogle Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock release gravity currents. Dyn. Atmos. Oceans 24, 183–195.CrossRefGoogle Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1993 Entrainment in turbulent gravity currents. Nature 362, 829–831.Google Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment in two dimensional and axisymmetric gravity currents. J. Fluid Mech. 308, 289–311.Google Scholar
Hogg, A. J., Nasr-Azadani, M. M., Ungarish, M. & Meiburg, E. 2016 Sustained gravity currents in a channel. J. Fluid Mech. 798, 853–888.CrossRefGoogle Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.Google Scholar
Huppert, H. E. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid Mech. 99, 785–799.CrossRefGoogle Scholar
Johnson, C. & Hogg, A. 2013 Entraining gravity currents. J. Fluid Mech. 731, 477–801.Google Scholar
Marino, B. M., Thomas, L. P. & Linden, P. F. 2005 The front condition for gravity currents. J. Fluid Mech. 536, 49–78.Google Scholar
Maxworthy, T. 1983 Gravity currents with variable inflow. J. Fluid Mech. 128, 247–257.CrossRefGoogle Scholar
Najafpour, N., Samie, M., Firoozabadi, B. & Afshin, H. 2014 Theoretical and experimental investigation of density jump on an inclined surface. Scientia Iranica B 21‐5, 1655–1665.Google Scholar
Nourmohammadi, Z., Afshin, H. & Firoozabadi, B. 2011 Experimental observation of the flow structure of turbidity currents. J. Hydraul Res. 49‐2, 168–177.CrossRefGoogle Scholar
Ottolenghi, L., Adduce, C., Inghilesi, R., Armenio, V. & Roman, F. 2016 Entrainment and mixing in unsteady gravity currents. J. Hydraul Res. 54, 541–557.Google Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.Google Scholar
Samasiri, P. & Woods, A. W. 2015 Mixing in axisymmetric gravity currents. J. Fluid Mech. 782, R1.Google Scholar
Sher, D. & Woods, A. W. 2015 Gravity currents: entrainment, stratification and self-similarity. J. Fluid Mech. 784, 130–162.CrossRefGoogle Scholar
Simpson, J. 1997 Gravity Currents. Cambridge University Press.Google Scholar
Slim, A. C. & Huppert, H. E. 2008 Gravity currents from a line source in an ambient flow. J. Fluid Mech. 606, 1–26.CrossRefGoogle Scholar
Turner, J. S. 1979 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Varjavand, P., Ghomeshi, M., Dalir, A. H., Farsadizadeh, D. & Gorgij, A. D. 2015 Experimental observation of saline underflows and turbidity currents, flowing over rough beds. Can. J. Civ. Engng 42, 834–844.Google Scholar