No CrossRef data available.
Published online by Cambridge University Press: 26 September 2023
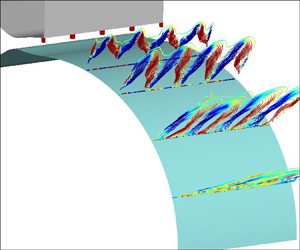
A highly compressive effect would suppress the mixing of the shear layer in a convex wall jet. The spanwise distributed protrusions at the nozzle lip are employed to achieve mixing enhancement in this study. The mixing characteristics and enhancement mechanisms are numerically investigated by the delayed detached-eddy simulation method based on the two-equation shear-stress transport model. A widely applicable flow spatiotemporal analysis method, called proper orthogonal decomposition (POD), is used to gain further insight into the dynamical behaviours of the flow instability mode. The results reveal that the centrifugal effect maintains and amplifies the initial perturbations induced by the spanwise distributed heterogeneities, resulting in forced streamwise vortices. The instabilities induced by the streamwise vortices significantly increase the growth rate of the jet half-width and the shear layer vorticity thickness. The spanwise wavelength of the streamwise vortices is consistent with the spanwise distributed forced excitation. In addition, the spanwise meandering motion of the streamwise vortices is observed, which is usually associated with the streamwise travelling wave. This is further confirmed by the POD analysis of the spanwise velocity fluctuation in both stream-radial and stream-span sections. Also, the spatial distributions of the POD modes with the highest energy provide information on the secondary instability modes. Both sinuous and varicose types of disturbances are observed in the unforced jet, whereas the forced jet seems to be dominated by the sinuous type instability, which is more easily excited than the varicose type instability. Moreover, the turbulence intensity in the forced jet is also significantly enhanced as expected due to the earlier and stronger streamwise vortices and associated instabilities. The enhanced turbulent characteristics of the highly compressible condition tend to be isotropic, whereas in the unforced jet, it is anisotropic due to the strong compressibility suppressing the spanwise turbulent fluctuations.