Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-22T14:34:33.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed convection in a periodically heated channel

Published online by Cambridge University Press:  03 March 2015

M. Z. Hossain  and
J. M. Floryan
M. Z. Hossain*
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, ON N6A 5B9, Canada
J. M. Floryan
Affiliation:
Department of Mechanical and Materials Engineering, The University of Western Ontario, London, Ontario, ON N6A 5B9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Mixed convection in a channel with flow driven by a pressure gradient and subject to spatially periodic heating along one of the walls has been studied. The pattern of the heating is characterized by the wavenumber ${\it\alpha}$ and its intensity is expressed in terms of the Rayleigh number 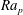$\mathit{Ra}_{p}$. The primary convection has the form of counter-rotating rolls with the wavevector parallel to the wavevector of the heating. The resulting net heat flow between the walls increases proportionally to 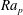$\mathit{Ra}_{p}$ but the growth saturates when 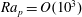$\mathit{Ra}_{p}=O(10^{3})$. The most effective heating pattern corresponds to 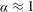${\it\alpha}\approx 1$, as this leads to the most intense transverse motion. The primary convection is subject to transition to secondary states with the onset conditions depending on ${\it\alpha}$. The conditions leading to transition between different forms of secondary motion have been determined using the linear stability theory. Three patterns of secondary motion may occur at small Reynolds numbers 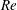$\mathit{Re}$, i.e. longitudinal rolls, transverse rolls and oblique rolls, with the critical conditions varying significantly as a function of ${\it\alpha}$. An increase of ${\it\alpha}$ leads to the elimination of the longitudinal rolls and, eventually, to the elimination of the oblique rolls, with the transverse rolls assuming the dominant role. For large ${\it\alpha}$, the transition is driven by the Rayleigh–Bénard mechanism; while for 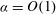${\it\alpha}=O(1)$, the spatial parametric resonance dominates. The global flow characteristics are identical regardless of whether the heating is applied at the lower or the upper wall.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 768 , 10 April 2015 , pp. 51 - 90
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.CrossRefGoogle Scholar
Beltrame, P., Knobloch, E., Hänggi, P. & Thiele, U. 2011 Rayleigh and depinning instabilities of forced liquid ridges on heterogeneous substrates. Phys. Rev. E 83, 016305.CrossRefGoogle ScholarPubMed
Bénard, H. 1900 Les tourbillons cellulaires dans une nappe liquide. Rev. Gén. Sci. Pure Appl. 11, 1261–1271.Google Scholar
Bloch, F. 1928 Über die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. 52, 555–600.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.CrossRefGoogle Scholar
Chilla, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58–82.CrossRefGoogle ScholarPubMed
Clever, R. M. & Busse, F. H. 1991 Instabilities of longitudinal rolls in the presence of Poiseuille flow. J. Fluid Mech. 229, 529–617.CrossRefGoogle Scholar
Coddington, E. A. & Levinson, N. 1965 Theory of Ordinary Differential Equations. McGraw-Hill.Google Scholar
Dubief, Y. & Delcayre, F. 2000 On coherent-vortex identification in turbulence. J. Turbul. 1, 011.CrossRefGoogle Scholar
Floryan, J. M. 1997 Stability of wall bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.CrossRefGoogle Scholar
Floryan, J. M. 2003 Vortex instability in a diverging–converging channel. J. Fluid Mech. 482, 17–50.CrossRefGoogle Scholar
Floryan, J. M. 2012 The thermo-superhydrophobic effect. Bull. Am. Phys. Soc. 57 (1), X50.00015.Google Scholar
Freund, G., Pesch, W. & Zimmermann, W. 2011 Rayleigh–Bénard convection in the presence of spatial temperature modulations. J. Fluid Mech. 673, 318–348.CrossRefGoogle Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33, 21–32.CrossRefGoogle Scholar
Hasnaoui, M., Rilgen, E., Vasseur, P. & Robillard, L. 1991 Mixed convective heat transfer in a horizontal channel heated periodically from below. Numer. Heat Transfer A 20, 297–315.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2013a Heat transfer due to natural convection in a periodically heated slot. Trans. ASME: J. Heat Transfer 135, 022503.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2013b Instabilities of natural convection in a periodically heated layer. J. Fluid Mech. 733, 33–67.CrossRefGoogle Scholar
Hossain, M. Z. & Floryan, J. M. 2014 Natural convection in a fluid layer periodically heated from above. Phys. Rev. E 90, 023015.CrossRefGoogle Scholar
Hossain, M. Z., Floryan, D. & Floryan, J. M. 2012 Drag reduction due to spatial thermal modulations. J. Fluid Mech. 713, 398–419.CrossRefGoogle Scholar
Howard, L. N. & Krishnamurti, R. 1986 Large-scale flow in turbulent convection: a mathematical model. J. Fluid Mech. 170, 385–410.CrossRefGoogle Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.CrossRefGoogle Scholar
Kelly, R. E. 1994 The onset and development of thermal convection in fully developed shear flows. Adv. Appl. Mech. 31, 35–112.CrossRefGoogle Scholar
Kelly, R. E. & Pal, D. 1976a Thermal convection induced between non-uniformly heated horizontal surfaces. In Proceedings of the 1976 Heat Transfer and Fluid Mechanics Institute, pp. 1–17. Stanford University Press.Google Scholar
Kelly, R. E. & Pal, D. 1976b Thermal convection with spatially periodic boundary conditions: resonant wavelength excitation. J. Fluid Mech. 86, 433–456.CrossRefGoogle Scholar
Koschmieder, E. L. 1993 Bénard Cells and Taylor Vortices. Cambridge University Press.Google Scholar
Krishnan, M., Ugaz, V. M. & Burns, M. A. 2002 PCR in a Rayleigh–Bénard convection cell. Science 298, 793.CrossRefGoogle Scholar
Lenardic, A., Moresi, L., Jellinek, A. M. & Manga, M. 2005 Continental insulation, mantle cooling, and the surface area of oceans and continents. Earth Planet. Sci. Lett. 234, 317–333.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Manor, A., Hagberg, A. & Meron, E. 2008 Wavenumber locking in spatially forced pattern-forming systems. Europhys. Lett. 83, 10005.CrossRefGoogle Scholar
Manor, R., Hagberg, A. & Meron, E. 2009 Wavenumber locking and pattern formation in spatially forced systems. New J. Phys. 11, 063016.CrossRefGoogle Scholar
Marcq, S. & Weiss, J. 2012 Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere. Cryosphere 6, 143–156.CrossRefGoogle Scholar
Maxworthy, T. 1997 Convection into domains with open boundaries. Annu. Rev. Fluid Mech. 29, 327–371.CrossRefGoogle Scholar
Pellew, A. & Southwell, R. V. 1940 On maintained convective motion in a fluid heated from below. Proc. R. Soc. Lond. A 176, 312–343.Google Scholar
Rayleigh, J. W. S. 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.CrossRefGoogle Scholar
Ripesi, P., Biferale, L., Sbragaglia, M. & Wirth, A. 2014 Natural convection with mixed insulating and conducting boundary conditions: low- and high-Rayleigh-number regimes. J. Fluid Mech. 742, 636–663.CrossRefGoogle Scholar
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.CrossRefGoogle Scholar
Weiss, S., Seiden, G. & Bodenschatz, E. 2012 Pattern formation in spatially forced thermal convection. New J. Phys. 14, 053010.CrossRefGoogle Scholar
Winters, K. B. & Young, W. R. 2009 Available potential energy and buoyancy variance in horizontal convection. J. Fluid Mech. 629, 221–230.CrossRefGoogle Scholar