Hostname: page-component-5cf477f64f-qls9x Total loading time: 0 Render date: 2025-04-02T21:31:13.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed convection in a horizontal duct with bottom heating and strong transverse magnetic field

Published online by Cambridge University Press:  19 September 2014

Xuan Zhang  and
Oleg Zikanov
Xuan Zhang
Affiliation:
Department of Mechanical Engineering, University of Michigan – Dearborn, MI 48128-1491, USA
Oleg Zikanov*
Affiliation:
Department of Mechanical Engineering, University of Michigan – Dearborn, MI 48128-1491, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

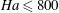Mixed convection in a horizontal duct with imposed transverse horizontal magnetic field is studied using direct numerical simulations (DNS) and linear stability analysis. The duct’s walls are electrically insulated and thermally insulated with the exception of the bottom wall, at which constant-rate heating is applied. The focus of the study is on flows at high Hartmann ($\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ha}\le 800$) and Grashof (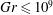$\mathit{Gr}\le 10^9$) numbers. It is found that, while conventional turbulence is fully suppressed, the natural convection mechanism leads to the development of large-scale coherent structures. Two types of flows are found. One is the ‘low-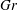$\mathit{Gr}$’ regime, in which the structures are rolls aligned with the magnetic field and velocity and temperature fields are nearly uniform along the magnetic field lines outside of the boundary layers. Another is the ‘high-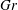$\mathit{Gr}$’ regime, in which the convection appears as a combination of similar rolls oriented along the magnetic field lines and streamwise-oriented rolls. In this case, velocity and temperature distributions are anisotropic, but three-dimensional.

JFM classification

Convection: Convection MHD and Electrohydrodynamics: High-Hartmann-number flows MHD and Electrohydrodynamics: MHD and Electrohydrodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 33 - 56
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alboussière, T., Garandet, J. P. & Moreau, R. 1993 Buoyancy-driven convection with a uniform magnetic field. Part 1. Asymptotic analysis. J. Fluid Mech. 253, 545–563.Google Scholar
Authié, G., Tagawa, T. & Moreau, R. 2003 Buoyant flow in long vertical enclosures in the presence of a strong horizontal magnetic field. Part 2. Finite enclosures. Eur. J. Mech. (B/Fluids) 22 (3), 203–220.Google Scholar
Branover, H. 1978 Magnetohydrodynamic Flow in Ducts. Wiley.Google Scholar
Davidson, P. A. 2001 An Introduction to Magnetohydrodynamics. Cambridge University Press.Google Scholar
Genin, L. G., Zhilin, V. G., Ivochkin, Y. P., Razuvanov, N. G., Belyaev, I. A., Listratov, Y. I. & Sviridov, V. G.2011 Temperature fluctuations in a heated horizontal tube affected by transverse magnetic field. In Proceedings of the 8th International Pamir Conference on Fundamental and Applied MHD, Borgo, Corsica, pp. 37–41.Google Scholar
Krasnov, D., Zikanov, O. & Boeck, T. 2011 Comparative study of finite difference approaches to simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number. Comput. Fluids 50, 46–59.CrossRefGoogle Scholar
Krasnov, D. S., Zikanov, O. & Boeck, T. 2012 Numerical study of magnetohydrodynamic duct flow at high Reynolds and Hartmann numbers. J. Fluid Mech. 704, 421–446.Google Scholar
Lee, D. & Choi, H. 2001 Magnetohydrodynamic turbulent flow in a channel at low magnetic Reynolds number. J. Fluid Mech. 429, 367–394.Google Scholar
Lyubimova, T. P., Lyubimov, D. V., Morozov, V. A., Scuridin, R. V., Hadid, H. B. & Henry, D. 2009 Stability of convection in a horizontal channel subjected to a longitudinal temperature gradient. Part 1. Effect of aspect ratio and Prandtl number. J. Fluid Mech. 635, 275–296.Google Scholar
Mas de les Valls, E., Batet, L., de Medina, V., Fradera, J. & Sedano, L. 2011 Qualification of MHD effects in dual-coolant DEMO blanket and approaches to their modelling. Fusion Engng Des. 86 (9–11), 2326–2329.Google Scholar
Mas de les Valls, E., Sedano, L., Batet, L., Ricapito, I., Aiello, A., Gastaldi, O. & Gabriel, F. 2008 Lead–lithium eutectic material database for nuclear fusion technology. J. Nucl. Mater. 376 (3), 353–357.CrossRefGoogle Scholar
Mistrangelo, C. & Bühler, L. 2013 Magneto-convective flows in electrically and thermally coupled channels. Fusion Engng Des. 88 (9–10), 2323–2327.Google Scholar
Molokov, S., Moreau, R. & Moffatt, H. K. 2007 Magnetohydrodynamics: Historical Evolution and Trends. Springer.Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143, 90–124.CrossRefGoogle Scholar
Ni, M.-J., Munipalli, R., Huang, P., Morley, N. B. & Abdou, M. A. 2007 A current density conservative scheme for incompressible MHD flows at a low magnetic Reynolds number. Part I: On a rectangular collocated grid system. J. Comput. Phys. 227, 174–204.Google Scholar
Smolentsev, S., Moreau, R. & Abdou, M. 2008 Characterization of key magnetohydrodynamic phenomena for PbLi flows for the US DCLL blanket. Fusion Engng Des. 83, 771–783.Google Scholar
Smolentsev, S., Moreau, R., Bühler, L. & Mistrangelo, C. 2010 MHD thermofluid issues of liquid–metal blankets: phenomena and advances. Fusion Engng Des. 85 (7–9), 1196–1205.Google Scholar
Smolentsev, S., Morley, M. & Abdou, M. 2006 MHD and thermal issues of the SiCf/SiC flowchannel insert. Fusion Sci. Technol. 50, 107–119.Google Scholar
Sommeria, J. & Moreau, R. 1982 Why, how and when MHD-turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.Google Scholar
Tagawa, T., Authié, G. & Moreau, R. 2002 Buoyant flow in long vertical enclosures in the presence of a strong horizontal magnetic field. Part 1. Fully-established flow. Eur. J. Mech. (B/Fluids) 21 (3), 383–398.Google Scholar
Vetcha, N., Smolentsev, S., Abdou, M. & Moreau, R. 2013 Study of instabilities and quasi-two-dimensional turbulence in volumetrically heated magnetohydrodynamic flows in a vertical rectangular duct. Phys. Fluids 25 (2), 024102.Google Scholar
Zhao, Y. & Zikanov, O. 2012 Instabilities and turbulence in magnetohydrodynamic flow in a toroidal duct prior to transition in Hartmann layers. J. Fluid Mech. 692, 288–316.CrossRefGoogle Scholar
Zikanov, O. 2010 Essential Computational Fluid Dynamics. Wiley.Google Scholar
Zikanov, O., Listratov, Y. & Sviridov, V. G. 2013 Natural convection in horizontal pipe flow with strong transverse magnetic field. J. Fluid Mech. 720, 486–516.Google Scholar
Zikanov, O. & Thess, A. 1998 Direct numerical simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.Google Scholar