Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T04:53:20.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Microstructure and rheology of finite inertia neutrally buoyant suspensions

Published online by Cambridge University Press:  16 May 2014

Hamed Haddadi  and
Jeffrey F. Morris
Hamed Haddadi
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
Jeffrey F. Morris*
Affiliation:
Benjamin Levich Institute and Department of Chemical Engineering, The City College of New York, New York, NY 10031, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The microstructure and rheological properties of suspensions of neutrally buoyant hard spherical particles in Newtonian fluid under finite inertia conditions are studied using the lattice-Boltzmann method (LBM), which is based on a discrete Boltzmann model for the fluid and Newtonian dynamics for the particles. 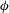The suspensions are subjected to simple-shear flow and the properties are studied as a function of Reynolds number and volume fraction, $\phi $. The inertia is characterized by the particle-scale shear flow Reynolds number 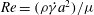$\mathit{Re}= {(\rho \dot{\gamma }a^{2})/\mu }$, where $a$ is the particle radius, 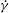$\dot{\gamma }$ is the shear rate and 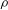$\rho $ and $\mu $ are the density and viscosity of the fluid, respectively. The influences of inertia and of the volume fraction are investigated for 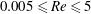$0.005\leqslant \mathit{Re}\leqslant 5$ and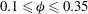$0.1\leqslant \phi \leqslant 0.35$. The flow-induced microstructure is studied using the pair distribution function 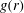$g(\boldsymbol {r})$. Different stress mechanisms, including those due to surface tractions (stresslet), acceleration and the Reynolds stress due to velocity fluctuations are computed and their influence on the first and second normal stress differences, the particle pressure and the viscosity of the suspensions are detailed. The probability density functions (PDFs) of linear and angular accelerations are also presented.

JFM classification

Complex Fluids: Complex Fluids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 749 , 25 June 2014 , pp. 431 - 459
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K. & Lu, Y. 1995 Lattice Boltzmann simulation of solid particles suspended in fluid. J. Stat. Phys. 81, 49–61.Google Scholar
Aidun, C. K., Lu, Y. & Ding, E. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.Google Scholar
Batchelor, G. K. 1970 The stress system in a suspension of force-free particles. J. Fluid Mech. 41, 545–570.Google Scholar
Bergenholtz, J., Brady, J. F. & Vicic, M. 2002 The non-Newtonian rheology of dilute colloidal suspensions. J. Fluid Mech. 456, 239–275.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brady, J. F. & Morris, J. F. 1997 Microstructure of strongly sheared suspensions and its impact on rheology and diffusion. J. Fluid Mech. 348, 103–139.Google Scholar
Drazer, G., Koplik, J., Khusid, B. & Acrivos, A. 2004 Microstructure and velocity fluctuations in sheared suspensions. J. Fluid Mech. 511, 237–263.Google Scholar
Feng, J., Hu, H. H. & Joseph, D. D. 1994 Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid part 1. Sedimentation. J. Fluid Mech. 261, 95–134.CrossRefGoogle Scholar
Humphry, K. J., Kulkarni, P. M., Weitz, D. A., Morris, J. F. & Stone, H. A. 2010 Axial and lateral particle ordering in finite Reynolds number channel flows. Phys. Fluids 22, 081703.CrossRefGoogle Scholar
Kossack, C. A. & Acrivos, A. 1974 Steady simple shear flow past a circular cylinder at moderate Reynolds numbers: a numerical solution. J. Fluid Mech. 66, 353–376.CrossRefGoogle Scholar
Kromkamp, J., Van den Ende, D. T. M., Kandhai, D., Van der Sman, R. G. M. & Boom, R. M. 2005 Shear-induced self-diffusion and microstructure in non-Brownian suspensions at non-zero Reynolds numbers. J. Fluid Mech. 529, 253–278.Google Scholar
Ku, D. N. 1997 Blood flow in arteries. Annu. Rev. Fluid Mech. 29, 399–434.Google Scholar
Kulkarni, P. M. & Morris, J. F. 2008a Pair-sphere trajectories in finite-Reynolds-number shear flow. J. Fluid Mech. 596, 413–435.CrossRefGoogle Scholar
Kulkarni, P. M. & Morris, J. F. 2008b Suspension properties at finite Reynolds number from simulated shear flow. Phys. Fluids 20, 040602.Google Scholar
Ladd, A. J. C. 1994a Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 271, 285–309.CrossRefGoogle Scholar
Ladd, A. J. C. 1994b Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 271, 311–339.Google Scholar
Lin, C., Peery, J. H. & Schowalter, W. R. 1970 Simple shear flow round a rigid sphere: inertial effects and suspension rheology. J. Fluid Mech. 44, 1–17.Google Scholar
Melrose, J. R. & Ball, R. C. 2004 Continuous shear thickening transitions in model concentrated colloids – the role of interparticle forces. J. Rheol. 48, 937–960.CrossRefGoogle Scholar
Mikulencak, D. R. & Morris, J. F. 2004 Stationary shear flow around fixed and free bodies at finite Reynolds number. J. Fluid Mech. 520, 215–242.Google Scholar
Nazockdast, E. & Morris, J. F. 2013 Microstructural theory and the rheology of concentrated colloidal suspensions. J. Fluid Mech. 713, 420–452.Google Scholar
Nguyen, N. Q. & Ladd, A. J. C. 2002 Lubrication corrections for lattice-Boltzmann simulations of particle suspensions. Phys. Rev. E 66, 046708.Google Scholar
Poe, G. G. & Acrivos, A. 1975 Closed-streamline flows past rotating single cylinders and spheres: inertia effects. J. Fluid Mech. 72, 605–623.Google Scholar
Robertson, C. R. & Acrivos, A. 1970 Low Reynolds number shear flow past a rotating circular cylinder. Part 1. Momentum transfer. J. Fluid Mech. 40, 685–703.Google Scholar
Sangani, A. S., Mo, G., Tsao, H. & Koch, D. L. 1996 Simple shear flows of dense gas–solid suspensions at finite Stokes numbers. J. Fluid Mech. 313, 309–341.CrossRefGoogle Scholar
Shakib-Manesh, A., Raiskinmaki, P., Koponen, A., Kataja, M. & Timonen, J. 2002 Shear stress in a couette flow of liquid–particle suspensions. J. Stat. Phys. 107, 67–84.Google Scholar
Sierou, A. & Brady, J. F. 2001 Accelerated stokesian dynamics simulations. J. Fluid Mech. 448, 115–146.Google Scholar
Sierou, A. & Brady, J. F. 2004 Rheology and microstructure in concentrated non-colloidal suspensions. J. Rheol. 46, 1031–1056.Google Scholar
Subramanian, G. & Brady, J. F. 2006 Trajectory analysis for non-Brownian inertial suspensions in simple shear flow. J. Fluid Mech. 559, 151–203.Google Scholar
Subramanian, G. & Koch, D. L. 2006a Inertial effects on the transfer of heat or mass from neutrally buoyant spheres in a steady linear velocity field. Phys. Fluids 18, 073302.Google Scholar
Subramanian, G. & Koch, D. L. 2006b Centrifugal forces alter streamline topology and greatly enhance the rate of heat and mass transfer from neutrally buoyant particles to a shear flow. Phys. Rev. Lett. 96, 134503.Google Scholar
Subramanian, G., Koch, D. L., Zhang, J. & Yang, C. 2011 The influence of the inertially dominated outer region on the rheology of a dilute dispersion of low-Reynolds-number drops or rigid particles. J. Fluid Mech. 674, 307–358.CrossRefGoogle Scholar
Vivek Raja, R., Subramanian, G. & Koch, D. L. 2010 Inertial effects on the rheology of a dilute emulsion. J. Fluid Mech. 646, 255–296.Google Scholar
Yan, Y., Morris, J. F. & Koplik, J. 2007 Hydrodynamic interaction of two particles in confined linear shear flow at finite Reynolds number. Phys. Fluids 19, 113305.CrossRefGoogle Scholar
Yeo, K. & Maxey, M. R. 2010 Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649, 205–231.Google Scholar
Yeo, K. & Maxey, M. R. 2013 Dynamics and rheology of concentrated, finite-Reynolds-number suspensions in a homogeneous shear flow. Phys. Fluids 25, 053303.Google Scholar
Zurita-Gotor, M., Blawzdziewicz, J. & Wajnryb, E. 2007 Swapping trajectories: a new wall-induced cross-streamline particle migration mechanism in a dilute suspension of spheres. J. Fluid Mech. 592, 447–469.Google Scholar