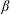 $\unicode[STIX]{x1D6FD}$-plane
$\unicode[STIX]{x1D6FD}$-planePublished online by Cambridge University Press: 26 February 2018
Observations, numerical simulations and theoretical scaling arguments suggest that in mid-latitudes, away from the source regions and the equator, the meridional transport of abyssal water masses along a continental slope corresponds to planetary geostrophic flows that are gravity- or density-driven and topographically steered. We investigate these dynamics using a nonlinear reduced-gravity model that can describe grounded abyssal meridional flow over sloping topography that crosses the planetary vorticity gradient. Exact nonlinear steady and time-dependent solutions are obtained. The general steady theory is illustrated for a non-parallel equatorward flow that possesses a single along-slope grounding along the upslope flank of the current (complementing previous work). Four specific nonlinear time-dependent solutions are described. Two initial-value problems are solved exactly. The first initial configuration corresponds to an equatorward abyssal flow that has no cross-slope shear in the along-slope velocity and possesses a single grounding along the upslope flank of the current. The nonlinear time-dependent evolution of this initial current into a non-parallel shear flow is described. The second initial condition corresponds to an isolated radially symmetric grounded abyssal pool or dome. The nonlinear time-dependent evolution of this abyssal dome, which propagates equatorward with unsteady along- and cross-slope velocities while deforming into an elliptically shaped abyssal dome with 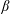 $\unicode[STIX]{x1D6FD}$-induced diminishing height, is described. Finally, the nonlinear time-dependent boundary-value problem can be solved exactly in which the in-flow boundary condition on the poleward boundary of the mid-latitude domain corresponds to a time-dependent abyssal current with both an upslope and downslope grounding. Two specific time-dependent boundary conditions are examined. The first corresponds to a time-limited surge in the equatorward volume transport in the abyssal current along the poleward boundary. The second configuration corresponds to the nonlinear evolution of a finite-amplitude downslope plume or loop that forms in the abyssal current that is reminiscent of those seen in baroclinic instability simulations.
$\unicode[STIX]{x1D6FD}$-induced diminishing height, is described. Finally, the nonlinear time-dependent boundary-value problem can be solved exactly in which the in-flow boundary condition on the poleward boundary of the mid-latitude domain corresponds to a time-dependent abyssal current with both an upslope and downslope grounding. Two specific time-dependent boundary conditions are examined. The first corresponds to a time-limited surge in the equatorward volume transport in the abyssal current along the poleward boundary. The second configuration corresponds to the nonlinear evolution of a finite-amplitude downslope plume or loop that forms in the abyssal current that is reminiscent of those seen in baroclinic instability simulations.