Published online by Cambridge University Press: 27 December 2018
We present new experimental data on the controls on the buoyancy flux in a stratified turbulent flow. The inner cylinder of an annulus of fluid with vertical axis is rotated to produce a turbulent flow field with Reynolds numbers of up to 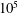 $10^{5}$, while a flux of saline fluid is supplied to the base of the tank, and an equal flux of fresh fluid is supplied to the top of the tank. In addition, fluid is vented from the base and the top of the tank with the same volume fluxes as the supply. The steady-state vertical flux of salt is explored. When the salt flux supplied to the base of the tank is very small, the tank becomes nearly well-mixed, and the vertical salt flux is approximately equal to one-half the source flux. As the source salt flux increases, a weak stable salinity gradient develops across the tank, and the vertical salt flux increases. As the source flux continues to increase, eventually the vertical salt flux reaches a maximum, and further increases in the source salt flux can lead to an increase in the vertical salinity gradient but not the vertical flux. We interpret the transition in the vertical buoyancy flux as representing a change from a source-limited regime, where the buoyancy flux and buoyancy frequency,
$10^{5}$, while a flux of saline fluid is supplied to the base of the tank, and an equal flux of fresh fluid is supplied to the top of the tank. In addition, fluid is vented from the base and the top of the tank with the same volume fluxes as the supply. The steady-state vertical flux of salt is explored. When the salt flux supplied to the base of the tank is very small, the tank becomes nearly well-mixed, and the vertical salt flux is approximately equal to one-half the source flux. As the source salt flux increases, a weak stable salinity gradient develops across the tank, and the vertical salt flux increases. As the source flux continues to increase, eventually the vertical salt flux reaches a maximum, and further increases in the source salt flux can lead to an increase in the vertical salinity gradient but not the vertical flux. We interpret the transition in the vertical buoyancy flux as representing a change from a source-limited regime, where the buoyancy flux and buoyancy frequency,  $N$, are related, to a mixing-limited regime, in which the buoyancy flux is independent of
$N$, are related, to a mixing-limited regime, in which the buoyancy flux is independent of 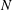 $N$. In the mixing-limited regime, the effective eddy diffusivity is proportional to
$N$. In the mixing-limited regime, the effective eddy diffusivity is proportional to 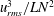 $u_{rms}^{3}/LN^{2}$ while in the source-limited regime, the eddy diffusivity is approximately proportional to
$u_{rms}^{3}/LN^{2}$ while in the source-limited regime, the eddy diffusivity is approximately proportional to 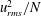 $u_{rms}^{2}/N$, where
$u_{rms}^{2}/N$, where 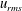 $u_{rms}$ and
$u_{rms}$ and 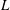 $L$ are the characteristic turbulence speed and length scale. This transition may have implications for the balance between upwelling and diapycnal mixing in the ocean, if the intensity of the turbulence varies in space or the flux of deep water varies in time.
$L$ are the characteristic turbulence speed and length scale. This transition may have implications for the balance between upwelling and diapycnal mixing in the ocean, if the intensity of the turbulence varies in space or the flux of deep water varies in time.