Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Landel, Julien R.
Caulfield, C. P.
and
Woods, Andrew W.
2012.
Streamwise dispersion and mixing in quasi-two-dimensional steady turbulent jets.
Journal of Fluid Mechanics,
Vol. 711,
Issue. ,
p.
212.
Mariotti, G.
Falcini, F.
Geleynse, N.
Guala, M.
Sun, T.
and
Fagherazzi, S.
2013.
Sediment eddy diffusivity in meandering turbulent jets: Implications for levee formation at river mouths.
Journal of Geophysical Research: Earth Surface,
Vol. 118,
Issue. 3,
p.
1908.
Peltier, Y.
Erpicum, S.
Archambeau, P.
Pirotton, M.
and
Dewals, B.
2014.
Meandering jets in shallow rectangular reservoirs: POD analysis and identification of coherent structures.
Experiments in Fluids,
Vol. 55,
Issue. 6,
Matulka, A.
López, P.
Redondo, J. M.
and
Tarquis, A.
2014.
On the entrainment coefficient in a forced plume: quantitative effects of source parameters.
Nonlinear Processes in Geophysics,
Vol. 21,
Issue. 1,
p.
269.
Chatanantavet, Phairot
and
Lamb, Michael P.
2014.
Sediment transport and topographic evolution of a coupled river and river plume system: An experimental and numerical study.
Journal of Geophysical Research: Earth Surface,
Vol. 119,
Issue. 6,
p.
1263.
Canestrelli, Alberto
Nardin, William
Edmonds, Douglas
Fagherazzi, Sergio
and
Slingerland, Rudy
2014.
Importance of frictional effects and jet instability on the morphodynamics of river mouth bars and levees.
Journal of Geophysical Research: Oceans,
Vol. 119,
Issue. 1,
p.
509.
Xu, Min-Yi
Tong, Xing-Qing
Yue, Dan-Ting
Zhang, Jian-Peng
Mi, Jian-Chun
J., Nathan G.
and
M., Kalt P. A.
2014.
Effect of noncircular orifice plates on the near flow field of turbulent free jets.
Chinese Physics B,
Vol. 23,
Issue. 12,
p.
124703.
Cafiero, Gioacchino
Discetti, Stefano
and
Astarita, Tommaso
2015.
Flow field topology of submerged jets with fractal generated turbulence.
Physics of Fluids,
Vol. 27,
Issue. 11,
Fagherazzi, Sergio
Edmonds, Douglas A.
Nardin, William
Leonardi, Nicoletta
Canestrelli, Alberto
Falcini, Federico
Jerolmack, Douglas J.
Mariotti, Giulio
Rowland, Joel C.
and
Slingerland, Rudy L.
2015.
Dynamics of river mouth deposits.
Reviews of Geophysics,
Vol. 53,
Issue. 3,
p.
642.
Mullyadzhanov, R.
Ilyushin, B.
Hadžiabdić, M.
and
Hanjalić, K.
2015.
Direct and Large-Eddy Simulation IX.
Vol. 20,
Issue. ,
p.
233.
Rocco, Stefano
and
Woods, Andrew W.
2015.
Dispersion in two-dimensional turbulent buoyant plumes.
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
Howard, Kevin B.
Singh, Arvind
Sotiropoulos, Fotis
and
Guala, Michele
2015.
On the statistics of wind turbine wake meandering: An experimental investigation.
Physics of Fluids,
Vol. 27,
Issue. 7,
Shestakov, Maxim V.
Dulin, Vladimir M.
Tokarev, Mikhail P.
Sikovsky, Dmitrii Ph.
and
Markovich, Dmitriy M.
2015.
PIV study of large-scale flow organisation in slot jets.
International Journal of Heat and Fluid Flow,
Vol. 51,
Issue. ,
p.
335.
Terashima, Osamu
Sakai, Yasuhiko
Nagata, Kouji
Ito, Yasumasa
Onishi, Kazuhiro
and
Shouji, Yuichi
2015.
On the velocity and pressure statistics during the flapping motion in a planar turbulent jet.
International Journal of Heat and Fluid Flow,
Vol. 53,
Issue. ,
p.
56.
Hanjalić, K.
and
Mullyadzhanov, R.
2015.
On spatial segregation of vortices and pressure eddies in a confined slot jet.
Physics of Fluids,
Vol. 27,
Issue. 3,
Righolt, B. W.
Kenjereš, S.
Kalter, R.
Tummers, M. J.
and
Kleijn, C. R.
2015.
Dynamics of an oscillating turbulent jet in a confined cavity.
Physics of Fluids,
Vol. 27,
Issue. 9,
Mullyadzhanov, R.
Ilyushin, B.
and
Hanjalić, K.
2015.
On dynamics and secondary currents in meandering confined turbulent shallow jet.
International Journal of Heat and Fluid Flow,
Vol. 56,
Issue. ,
p.
284.
Cafiero, Gioacchino
Greco, Carlo Salvatore
Astarita, Tommaso
and
Discetti, Stefano
2016.
Flow field features of fractal impinging jets at short nozzle to plate distances.
Experimental Thermal and Fluid Science,
Vol. 78,
Issue. ,
p.
334.
Burridge, H.C.
Partridge, J.L.
and
Linden, P.F.
2016.
The Fluxes and Behaviour of Plumes Inferred from Measurements of Coherent Structures within Images of the Bulk Flow.
Atmosphere-Ocean,
Vol. 54,
Issue. 4,
p.
403.
Shestakov, M. V.
Mullyadzhanov, R. I.
Tokarev, M. P.
and
Markovich, D. M.
2016.
Modulation of large-scale meandering and three-dimensional flows in turbulent slot jets.
Journal of Engineering Thermophysics,
Vol. 25,
Issue. 2,
p.
159.
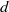 into a fluid confined between two relatively close rigid boundaries with gap
into a fluid confined between two relatively close rigid boundaries with gap 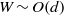 . At large vertical distances
. At large vertical distances 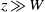 the jet structure consists of a meandering core with large counter-rotating eddies, which develop on alternate sides of the core. Using particle image velocimetry, we observe an inverse cascade typical of quasi-two-dimensional turbulence where both the core and the eddies grow linearly with
the jet structure consists of a meandering core with large counter-rotating eddies, which develop on alternate sides of the core. Using particle image velocimetry, we observe an inverse cascade typical of quasi-two-dimensional turbulence where both the core and the eddies grow linearly with  and travel at an average speed proportional to
and travel at an average speed proportional to 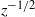 . However, although the present study concerns quasi-two-dimensional confined jets, the jets are self-similar and the mean properties are consistent with both experimental results and theoretical models of the time-averaged properties of fully unconfined planar two-dimensional jets. We believe that the dynamics of the interacting core and large eddies accounts for the Gaussian profile of the mean vertical velocity as shown by the spatial statistical distribution of the core and eddy structure. The lateral excursions (caused by the propagating eddies) of this high-speed central core produce a Gaussian distribution for the time-averaged vertical velocity. In addition, we find that approximately 75 % of the total momentum flux of the jet is contained within the core. The eddies travel substantially slower (at approximately 25 % of the maximum speed of the core) at each height and their growth is primarily attributed to entrainment of ambient fluid. The frequency of occurrence of the eddies decreases in a stepwise manner due to merging, with a well-defined minimum value of the corresponding Strouhal number
. However, although the present study concerns quasi-two-dimensional confined jets, the jets are self-similar and the mean properties are consistent with both experimental results and theoretical models of the time-averaged properties of fully unconfined planar two-dimensional jets. We believe that the dynamics of the interacting core and large eddies accounts for the Gaussian profile of the mean vertical velocity as shown by the spatial statistical distribution of the core and eddy structure. The lateral excursions (caused by the propagating eddies) of this high-speed central core produce a Gaussian distribution for the time-averaged vertical velocity. In addition, we find that approximately 75 % of the total momentum flux of the jet is contained within the core. The eddies travel substantially slower (at approximately 25 % of the maximum speed of the core) at each height and their growth is primarily attributed to entrainment of ambient fluid. The frequency of occurrence of the eddies decreases in a stepwise manner due to merging, with a well-defined minimum value of the corresponding Strouhal number 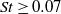 .
.

