Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T06:18:55.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean flow stability analysis of oscillating jet experiments

Published online by Cambridge University Press:  19 September 2014

Kilian Oberleithner ,
Lothar Rukes  and
Julio Soria
Kilian Oberleithner*
Affiliation:
Institut für Strömungsmechanik und Technische Akustik, HFI, Technische Universität Berlin, 10623 Berlin, Germany
Lothar Rukes
Affiliation:
Institut für Strömungsmechanik und Technische Akustik, HFI, Technische Universität Berlin, 10623 Berlin, Germany
Julio Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace & Combustion, Monash University, Melbourne, VIC 3800, Australia Department of Aeronautical Engineering, King Abdulaziz University, Jeddah, Kingdom of Saudi Arabia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear stability analysis (LSA) is applied to the mean flow of an oscillating round jet with the aim of investigating the robustness and accuracy of mean flow stability wave models. The jet’s axisymmetric mode is excited at the nozzle lip through a sinusoidal modulation of the flow rate at amplitudes ranging from 0.1 % to 100 %. The instantaneous flow field is measured via particle image velocimetry (PIV) and decomposed into a mean and periodic part utilizing proper orthogonal decomposition (POD). Local LSA is applied to the measured mean flow adopting a weakly non-parallel flow approach. The resulting global perturbation field is carefully compared with the measurements in terms of spatial growth rate, phase velocity, and phase and amplitude distribution. It is shown that the stability wave model accurately predicts the excited flow oscillations during their entire growth phase and during a large part of their decay phase. The stability wave model applies over a wide range of forcing amplitudes, showing no pronounced sensitivity to the strength of nonlinear saturation. The upstream displacement of the neutral point and the successive reduction of gain with increasing forcing amplitude is very well captured by the stability wave model. At very strong forcing (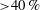$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{>}40\, \%$), the flow becomes essentially stable to the axisymmetric mode. For these extreme cases, the prediction deteriorates from the measurements due to an interaction of the forced wave with the geometric confinement of the nozzle. Moreover, the model fails far downstream in a region where energy is transferred from the oscillation back to the mean flow. This study supports previously conducted mean flow stability analysis of self-excited flow oscillations in the cylinder wake and in the vortex breakdown bubble and extends the methodology to externally forced convectively unstable flows. The high accuracy of mean flow stability wave models as demonstrated here is of great importance for the analysis of coherent structures in turbulent shear flows.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 1 - 32
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Cater, J. E. & Soria, J. 2002 The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 472, 167–200.CrossRefGoogle Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.CrossRefGoogle Scholar
Cooper, A. J. & Peake, N. 2002 The stability of a slowly diverging swirling jet. J. Fluid Mech. 473, 389–411.CrossRefGoogle Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77, 397–413.CrossRefGoogle Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48, 547–591.CrossRefGoogle Scholar
Edgington-Mitchell, D., Oberleithner, K., Honnery, D. R. & Soria, J. 2014 Coherent structure and sound production in the helical mode of a screeching axisymmetric jet. J. Fluid Mech. 748, 822–847.CrossRefGoogle Scholar
Gaster, M., Kit, E. & Wygnanski, I. 1985 Large-scale structures in a forced turbulent mixing layer. J. Fluid Mech. 150, 23–39.CrossRefGoogle Scholar
Greenblatt, D. & Wygnanski, I. J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36 (7), 487–545.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.CrossRefGoogle Scholar
Huang, H. T., Fiedler, H. E. & Wang, J. J. 1993 Limitation and improvement of PIV. Exp. Fluids 15 (4–5), 263–273.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Juniper, M. P., Tammisola, O. & Lundell, F. 2011 The local and global stability of confined planar wakes at intermediate Reynolds number. J. Fluid Mech. 686, 218–238.CrossRefGoogle Scholar
Khorrami, M. R., Malik, M. R. & Ash, R. L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81 (1), 206–229.CrossRefGoogle Scholar
Lifshitz, Y., Degani, D. & Tumin, A. 2008 On the interaction of turbulent shear layers with harmonic perturbations. Flow Turbul. Combust. 80 (1), 61–80.CrossRefGoogle Scholar
Marasli, B., Champagne, F. H. & Wygnanski, I. J. 1991 On linear evolution of unstable disturbances in a plane turbulent wake. Phys. Fluids 3, 665–674.CrossRefGoogle Scholar
Meliga, P., Pujals, G. & Serre, É. 2012 Sensitivity of 2-d turbulent flow past a $d$ -shaped cylinder using global stability. Phys. Fluids 24 (6), 061701.CrossRefGoogle Scholar
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. 2003 A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C. O., Seele, R. & Wygnanski, I. 2012 Formation of turbulent vortex breakdown: intermittency, criticality, and global instability. AIAA J. 50, 1437–1452.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C. O. & Wygnanski, I. 2014 On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.CrossRefGoogle Scholar
Oberleithner, K., Sieber, M., Nayeri, C. N., Paschereit, C. O., Petz, C., Hege, H.-C., Noack, B. R. & Wygnanski, I. 2011 Three-dimensional coherent structures in a swirling jet undergoing vortex breakdown: stability analysis and empirical mode construction. J. Fluid Mech. 679, 383–414.CrossRefGoogle Scholar
O’Neill, P., Soria, J. & Honnery, D. 2004 The stability of low Reynolds number round jets. Exp. Fluids 36, 473–483.CrossRefGoogle Scholar
Orszag, S. A. S. & Crow, S. C. S. 1970 Instability of a vortex sheet leaving a semi-infinite plate (vortex sheet instability leaving semiinfinite flat plate, considering boundary effects). Stud. Appl. Maths 49, 167–181.CrossRefGoogle Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.CrossRefGoogle Scholar
Reau, N. & Tumin, A. 2002 Harmonic perturbations in turbulent wakes. AIAA J. 40, 526–530.CrossRefGoogle Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54, 263–288.CrossRefGoogle Scholar
Rienstra, S. 1983 A small strouhal number analysis for acoustic wave-jet flow-pipe interaction. J. Sound Vib. 86 (4), 539–556.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Sipp, D., Marquet, O., Meliga, P. & Barbagallo, A. 2010 Dynamics and control of global instabilities in open-flows: a linearized approach. Appl. Mech. Rev. 63 (3), 030801.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths XLV, 561–571.CrossRefGoogle Scholar
Soria, J.1994 Digital cross-correlation particle image velocimetry measurements in the near wake of a circular cylinder. In International Colloquium on Jets, Wakes and Shear Layers, Melbourne, Australia.Google Scholar
Soria, J. 1996a An adaptive cross-correlation digital PIV technique for unsteady flow investigations. In Proceedings 1st Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion (ed. Masri, A. & Honnery, D.), pp. 29–48. University of Sydney.Google Scholar
Soria, J. 1996b An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12, 221–233.CrossRefGoogle Scholar
Soria, J.1998 Multigrid approach to cross-correlation digital PIV and HPIV analysis. In Proceedings of 13th Australasian Fluid Mechanics Conference, Monash University, Melbourne, Australia.Google Scholar
Soria, J., Cater, J. & Kostas, J. 1999 High resolution multigrid cross-correlation digital PIV measurements of a turbulent starting jet using half frame image shift film recording. Opt. Laser Technol. 31, 3–12.CrossRefGoogle Scholar
Stöhr, M., Sadanandan, R. & Meier, W. 2011 Phase-resolved characterization of vortex–flame interaction in a turbulent swirl flame. Exp. Fluids 51, 1153–1167.CrossRefGoogle Scholar
Strange, P. J. R. & Crighton, D. G. 1983 Spinning modes on axisymmetric jets. I. J. Fluid Mech. 134, 231–245.CrossRefGoogle Scholar
von Ellenrieder, K., Kostas, J. & Soria, J. 2001 Measurements of a wall-bounded turbulent, separated flow using HPIV. J. Turbul. 2, 1–15.CrossRefGoogle Scholar
Weisbrot, I. & Wygnanski, I. 1988 On coherent structures in a highly excited mixing layer. J. Fluid Mech. 195, 137–159.CrossRefGoogle Scholar