Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T13:20:50.768Z Has data issue: false hasContentIssue false
  • English
  • Français

Marginally stable and turbulent boundary layers in low-curvature Taylor–Couette flow

Published online by Cambridge University Press:  15 February 2017

Hannes J. Brauckmann Open the ORCID record for Hannes J. Brauckmann [Opens in a new window]  and
Bruno Eckhardt
Hannes J. Brauckmann
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany
Bruno Eckhardt*
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany J. M. Burgerscentrum, Delft University of Technology, Mekelweg 2, 2628 CD Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Marginal stability arguments are used to describe the rotation number dependence of torque in Taylor–Couette (TC) flow for radius ratios 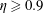$\unicode[STIX]{x1D702}\geqslant 0.9$ and shear Reynolds number 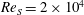$\mathit{Re}_{S}=2\times 10^{4}$. With an approximate representation of the mean profile by piecewise linear functions, characterised by the boundary-layer thicknesses at the inner and outer cylinder and the angular momentum in the centre, profiles and torques are extracted from the requirement that the boundary layers represent marginally stable TC subsystems and that the torque at the inner and outer cylinder coincide. This model then explains the broad shoulder in the torque as a function of rotation number near 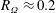$R_{\unicode[STIX]{x1D6FA}}\approx 0.2$. For rotation numbers 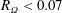$R_{\unicode[STIX]{x1D6FA}}<0.07$ the TC stability conditions predict boundary layers in which the shear Reynolds numbers are very large. Assuming that the TC instability is bypassed by some shear instability, a second narrower maximum in torque appears, in very good agreement with numerical simulations. The results show that marginal stability theory, despite its shortcomings in other cases, can explain quantitatively the non-monotonic torque variation with rotation number for both the broad maximum as well as the narrow maximum.

JFM classification

Boundary Layers: Boundary layer stability Turbulent Flows: Rotating turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 815 , 25 March 2017 , pp. 149 - 168
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barcilon, A. & Brindley, J. 1984 Organized structures in turbulent Taylor–Couette flow. J. Fluid Mech. 143, 429–449.CrossRefGoogle Scholar
Brauckmann, H. J. & Eckhardt, B. 2013a Direct numerical simulations of local and global torque in Taylor–Couette flow up to Re = 30 000. J. Fluid Mech. 718, 398–427.Google Scholar
Brauckmann, H. J. & Eckhardt, B. 2013b Intermittent boundary layers and torque maxima in Taylor–Couette flow. Phys. Rev. E 87 (3), 033004.Google Scholar
Brauckmann, H. J., Salewski, M. & Eckhardt, B. 2016 Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 790, 419–452.Google Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability, 1st edn. Clarendon.Google Scholar
Dong, S. 2007 Direct numerical simulation of turbulent Taylor–Couette flow. J. Fluid Mech. 587, 373–393.CrossRefGoogle Scholar
Donnelly, R. J. & Fultz, D. 1960 Experiments on the stability of viscous flow between rotating cylinders. II. Visual observations. Proc. R. Soc. Lond. A 258, 101–123.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.CrossRefGoogle Scholar
Dubrulle, B. & Hersant, F. 2002 Momentum transport and torque scaling in Taylor–Couette flow from an analogy with turbulent convection. Eur. Phys. J. B 26, 379–386.CrossRefGoogle Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Esser, A. & Grossmann, S. 1996 Analytic expression for Taylor–Couette stability boundary. Phys. Fluids 8 (7), 1814–1819.Google Scholar
Faisst, H. & Eckhardt, B. 2000 Transition from the Couette–Taylor system to the plane Couette system. Phys. Rev. E 61, 7227–7230.Google Scholar
van Gils, D. P. M., Huisman, S. G., Bruggert, G.-W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co- and counterrotating cylinders. Phys. Rev. Lett. 106, 024502.Google Scholar
van Gils, D. P. M., Huisman, S. G., Grossmann, S., Sun, C. & Lohse, D. 2012 Optimal Taylor–Couette turbulence. J. Fluid Mech. 706, 118–149.CrossRefGoogle Scholar
Gol’dshtik, M. A., Sapozhnikov, V. A. & Shtern, V. N. 1970 Verification of the Malkus hypothesis regarding the stability of turbulent flows. Fluid Dyn. 5 (5), 863–867.Google Scholar
Guseva, A., Willis, A. P., Hollerbach, R. & Avila, M. 2015 Transition to magnetorotational turbulence in Taylor–Couette flow with imposed azimuthal magnetic field. New J. Phys. 17, 093018.Google Scholar
Howard, L. N. 1966 Convection at high Rayleigh number. In Applied Mechanics, pp. 1109–1115. Springer.Google Scholar
King, G. P., Li, Y., Lee, W., Swinney, H. L. & Marcus, P. S. 1984 Wave speeds in wavy Taylor-vortex flow. J. Fluid Mech. 141, 365–390.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992a Transition to shear-driven turbulence in Couette–Taylor flow. Phys. Rev. A 46, 6390–6405.Google Scholar
Lathrop, D. P., Fineberg, J. & Swinney, H. L. 1992b Turbulent flow between concentric rotating cylinders at large Reynolds number. Phys. Rev. Lett. 68, 1515–1518.CrossRefGoogle ScholarPubMed
Lewis, G. S. & Swinney, H. L. 1999 Velocity structure functions, scaling, and transitions in high-Reynolds-number Couette–Taylor flow. Phys. Rev. E 59, 5457–5467.Google ScholarPubMed
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Malkus, W. V. R. 1956 Outline of a theory of turbulent shear flow. J. Fluid Mech. 1, 521–539.Google Scholar
Malkus, W. V. R. 1983 The amplitude of turbulent shear flow. Pure Appl. Geophys. 121 (3), 391–400.CrossRefGoogle Scholar
Marcus, P. S. 1984a Simulation of Taylor–Couette flow. Part 1. Numerical methods and comparison with experiment. J. Fluid Mech. 146, 45–64.Google Scholar
Marcus, P. S. 1984b Simulation of Taylor–Couette flow. Part 2. Numerical results for wavy-vortex flow with one travelling wave. J. Fluid Mech. 146, 65–113.CrossRefGoogle Scholar
Martínez-Arias, B., Peixinho, J., Crumeyrolle, O. & Mutabazi, I. 2014 Effect of the number of vortices on the torque scaling in Taylor–Couette flow. J. Fluid Mech. 748, 756–767.CrossRefGoogle Scholar
Merbold, S., Brauckmann, H. J. & Egbers, C. 2013 Torque measurements and numerical determination in differentially rotating wide gap Taylor–Couette flow. Phys. Rev. E 87, 023014.Google Scholar
Meseguer, A., Avila, M., Mellibovsky, F. & Marques, F. 2007 Solenoidal spectral formulations for the computation of secondary flows in cylindrical and annular geometries. Eur. Phys. J. Spec. Top. 146, 249–259.Google Scholar
Nagata, M. 1986 Bifurcations in Couette flow between almost corotating cylinders. J. Fluid Mech. 169, 229–250.CrossRefGoogle Scholar
Ostilla, R., Stevens, R. J. A. M., Grossmann, S., Verzicco, R. & Lohse, D. 2013 Optimal Taylor–Couette flow: direct numerical simulations. J. Fluid Mech. 719, 14–46.Google Scholar
Ostilla-Mónico, R., Huisman, S. G., Jannink, T. J. G., van Gils, D. P. M., Verzicco, R., Grossmann, S., Sun, C. & Lohse, D. 2014a Optimal Taylor–Couette flow: radius ratio dependence. J. Fluid Mech. 747, 1–29.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014b Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26 (1), 015114.Google Scholar
Paoletti, M. S., van Gils, D. P. M., Dubrulle, B., Sun, C., Lohse, D. & Lathrop, D. P. 2012 Angular momentum transport and turbulence in laboratory models of Keplerian flows. Astron. Astrophys. 547 (A64), 1–11.Google Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Angular momentum transport in turbulent flow between independently rotating cylinders. Phys. Rev. Lett. 106, 024501.Google Scholar
Rayleigh Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Reynolds, W. C. & Tiederman, W. G. 1967 Stability of turbulent channel flow, with application to Malkus’s theory. J. Fluid Mech. 27 (2), 253–272.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2000 Boundary-Layer Theory, 8th edn. Springer.Google Scholar
Smith, G. P. & Townsend, A. A. 1982 Turbulent Couette flow between concentric cylinders at large Taylor numbers. J. Fluid Mech. 123, 187–217.CrossRefGoogle Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Taylor, G. I. 1935 Distribution of velocity and temperature between concentric rotating cylinders. Proc. R. Soc. Lond. A 151, 494–512.Google Scholar
Wattendorf, F. L. 1935 A study of the effect of curvature on fully developed turbulent flow. Proc. R. Soc. Lond. A 148, 565–598.Google Scholar