Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T08:50:30.785Z Has data issue: false hasContentIssue false
  • English
  • Français

Marangoni-enhanced capillary wetting in surfactant-driven superspreading

Published online by Cambridge University Press:  14 September 2018

Hsien-Hung Wei Open the ORCID record for Hsien-Hung Wei [Opens in a new window]
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Superspreading is a phenomenon such that a drop of a certain class of surfactant on a substrate can spread with a radius that grows linearly with time much faster than the usual capillary wetting. Its origin, in spite of many efforts, is still not fully understood. Previous modelling and simulation studies (Karapetsas et al. J. Fluid Mech., vol. 670, 2011, pp. 5–37; Theodorakis et al. Langmuir, vol. 31, 2015, pp. 2304–2309) suggest that the transfer of the interfacial surfactant molecules onto the substrate in the vicinity of the contact line plays a crucial role in superspreading. Here, we construct a detailed theory to elaborate on this idea, showing that a rational account for superspreading can be made using a purely hydrodynamic approach without involving a specific surfactant structure or sorption kinetics. Using this theory it can be shown analytically, for both insoluble and soluble surfactants, that the curious linear spreading law can be derived from a new dynamic contact line structure due to a tiny surfactant leakage from the air–liquid interface to the substrate. Such a leak not only establishes a concentrated Marangoni shearing toward the contact line at a rate much faster than the usual viscous stress singularity, but also results in a microscopic surfactant-devoid zone in the vicinity of the contact line. The strong Marangoni shearing then turns into a local capillary force in the zone, making the contact line in effect advance in a surfactant-free manner. This local Marangoni-driven capillary wetting in turn renders a constant wetting speed governed by the de Gennes–Cox–Voinov law and hence the linear spreading law. We also determine the range of surfactant concentration within which superspreading can be sustained by local surfactant leakage without being mitigated by the contact line sweeping, explaining why only limited classes of surfactants can serve as superspreaders. We further show that spreading of surfactant spreaders can exhibit either the 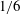$1/6$ or 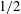$1/2$ power law, depending on the ability of interfacial surfactant to transfer/leak to the bulk/substrate. All these findings can account for a variety of results seen in experiments (Rafai et al. Langmuir, vol. 18, 2002, pp. 10486–10488; Nikolov & Wasan, Adv. Colloid Interface Sci., vol. 222, 2015, pp. 517–529) and simulations (Karapetsas et al. 2011). Analogy to thermocapillary spreading is also made, reverberating the ubiquitous role of the Marangoni effect in enhancing dynamic wetting driven by non-uniform surface tension.

JFM classification

Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 181 - 209
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beacham, D. R., Matar, O. K. & Craster, R. V. 2009 Wetting and surfactant-enhanced rapid spreading of drops on solid surfaces. Langmuir 25, 14174–14181.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolly, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–803.Google Scholar
Chan, K. Y. & Borhan, A. 2006 Spontaneous spreading of surfactant-bearing drops in the sorption-controlled limit. J. Colloid Interface Sci. 302, 374–377.Google Scholar
Chaudhury, K. & Chakraborty, S. 2015 Spreading of a droplet over a nonisothermal substrate: multiple scaling regines. Langmuir 31, 4196–4175.Google Scholar
Chesters, A. K. & Elyousfi, A. B. 1998 The influence of surfactants on the hydrodynamics of surface wetting. I. Nondiffusing limit. J. Colloid Interface Sci. 207, 20–29.Google Scholar
Clay, M. A. & Miksis, M. 2004 Effects of surfactant on droplet spreading. Phys. Fluids 16, 3070.Google Scholar
Cox, R. G. 1986a The dynamics of spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Cox, R. G. 1986b The dynamics of spreading of liquids on a solid surface. Part 2. Surfactants. J. Fluid Mech. 168, 195–220.Google Scholar
Ehrhard, P. 1993 Experiments on isothermal and non-isothermal spreading. J. Fluid Mech. 257, 463–483.Google Scholar
Ehrhard, P. & Davis, S. H. 1991 Non-isothermal spreading of liquid drops on horizontal plates. J. Fluid Mech. 229, 365–388.Google Scholar
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
Hill, R. M. 1988 Superspreading. Curr. Opin. Colloid Interface Sci. 3, 247–254.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35, 85–101.Google Scholar
Ivanova, N. A., Zhantenova, Z. B. & Starov, V. M. 2012 Wetting dynamics of polyoxyethylene alkyl ethers and trisiloxanes in respect polyoxyethylene chains and properties of substrates. Colloids Surfaces A 413, 307–313.Google Scholar
Jensen, O. E. & Grotberg, J. B. 1992 Insoluble surfactant spreading on a thin viscous film: shock evolution and film rupture. J. Fluid Mech. 240, 259–288.Google Scholar
Jensen, O. E. & Naire, S. 2006 The spreading and stability of a surfactant-laden drop on a prewetted substrate. J. Fluid Mech. 554, 5–24.Google Scholar
Joanny, J. F. 1989 Kinetics of spreading of a liquid supporting surfactant monolayer: repulsive solid surfaces. J. Colloid Interface Sci. 128, 407–415.Google Scholar
Karapetsas, G., Craster, R. V. & Matar, O. K. 2011 On surfactant-enhanced spreading and superspreading of liquid drops on solid surfaces. J. Fluid Mech. 670, 5–37.Google Scholar
Karapetsas, G., Sahu, K. C., Sefiane, K. & Matar, O. K. 2014 Thermocapillary-driven motion of a sessile drop: effect of non-monotonic dependence of surface tension on temperature. Langmuir 30, 4310–4321.Google Scholar
Kim, H.-Y., Qin, Y. & Fichthorn, K. A. 2006 Molecular dynamics simulations of nanodroplet spreading enhanced by linear surfactants. J. Chem. Phys. 125, 174708.Google Scholar
Kumar, N., Couzis, A. & Maldarelli, C. 2003b Measurement of the kinetic rate constants for the adsorption of superspreading trisiloxanes to an air/aqueous interface and the relevance of these measurements to the mechanism of superspreading. J. Colloid Interface Sci. 267, 272–285.Google Scholar
Kumar, N., Varanasi, K., Tilton, R. D. & Garoff, S. 2003a Surfactant self- assembly ahead of the contact line on a hydrophobic surface and its implications for wetting. Langmuir 19, 5366–5373.Google Scholar
Maldarelli, C. 2011 On the microhydrodynamics of superspreading. J. Fluid Mech. 670, 1–4.Google Scholar
Nikolov, A. & Wasan, D. 2015 Current opinion in superspreading mechanisms. Adv. Colloid Interface Sci. 222, 517–529.Google Scholar
Nikolov, A. D., Wasan, D. T., Chengara, A., Koczo, K., Policello, G. A. & Kolossvary, I. 2002 Superspreading driven by Marangoni flow. Adv. Colloid Interface Sci. 96, 325–338.Google Scholar
Rafai, S. & Bonn, D. 2005 Spreading of non-Newtonian fluids and surfactant solutions on solid surfaces. Physica A 358, 58–67.Google Scholar
Rafai, S., Sarker, D., Bergeron, V., Meunier, J. & Bonn, D. 2002 Superspreading: aqueous surfactant drops spreading on hydrophobic surfaces. Langmuir 18, 10486–10488.Google Scholar
Rame, E. 2001 The spreading of surfactant-laden liquids with surfactant transfer through the contact line. J. Fluid Mech. 440, 205–234.Google Scholar
Semenov, S., Trybala, A., Agogo, H., Kovalchuk, N., Ortega, F., Rubio, R. G., Starov, V. M. & Velarde, M. G. 2013 Evaporation of droplets of surfactant solutions. Langmuir 29, 10028–10036.Google Scholar
Smith, M. 1995 Thermocapillary migration of a two-dimensional liquid droplet on a solid surface. J. Fluid Mech. 294, 209–230.Google Scholar
Snoeijer, J. H. 2006 Free-surface flows with large slopes: beyond lubrication theory. Phys. Fluids 18, 021701.Google Scholar
Starov, V. M., de Ryck, A. & Velarde, M. G. 1997 On the Spreading of an insoluble surfactant over a thin viscous liquid layer. J. Colloid Interface Sci. 190, 104–113.Google Scholar
Stoebe, T., Lin, Z., Hill, R. M., Wards, M. D. & Davis, H. T. 1996 Surfactant-enhanced spreading. Langmuir 12, 337–344.Google Scholar
Stoebe, T., Lin, Z., Hill, R. M., Wards, M. D. & Davis, H. T. 1997 Enhanced spreading of aqueous films containing ethoxylated alcohol surfactants on solid substrates. Langmuir 13, 7270–7275.Google Scholar
Sui, Y. & Splet, P. D. M. 2015 Non-isothermal droplet spreading/dewetting and its reversal. J. Fluid Mech. 776, 74–95.Google Scholar
Tanner, L. H. 1979 The spreading of silicone oil drops on horizontal surfaces. J. Phys. 12, 1473.Google Scholar
Theodorakis, P. E., Müller, E. A., Craster, R. V. & Matar, O. K. 2015 Superspreading: mechanisms and molecular design. Langmuir 31, 2304–2309.Google Scholar
Voniov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11, 714–721.Google Scholar
Wang, X., Chen, L., Bonaccurso, E. & Venzmer, J. 2013 Dynamic wetting hydrophobic polymers by aqueous surfactant and superspreader solutions. Langmuir 29, 14855–14864.Google Scholar
Zhu, S., Miller, W. G., Scriven, L. E. & Davis, H. T. 1994 Superspreading of water-silicone surfactant on hydrophobic surfaces. Colloids Surface A 90, 63–78.Google Scholar