Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T01:21:06.293Z Has data issue: false hasContentIssue false
  • English
  • Français

Macroscopic model for unsteady flow in porous media

Published online by Cambridge University Press:  10 January 2019

Didier Lasseux Open the ORCID record for Didier Lasseux [Opens in a new window] ,
Francisco J. Valdés-Parada Open the ORCID record for Francisco J. Valdés-Parada [Opens in a new window]  and
Fabien Bellet Open the ORCID record for Fabien Bellet [Opens in a new window]
Didier Lasseux*
Affiliation:
CNRS, I2M, UMR 5295, Esplanade des Arts et Métiers, 33405 Talence CEDEX, France
Francisco J. Valdés-Parada
Affiliation:
Universidad Autónoma Metropolitana-Iztapalapa, Departamento de Ingeniería de Procesos e Hidráulica, Av. San Rafael Atlixco 186, 09340 Ciudad de México, Mexico
Fabien Bellet
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 3 rue Joliot Curie, 91192 Gif-sur-Yvette CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The present article reports on a formal derivation of a macroscopic model for unsteady one-phase incompressible flow in rigid and periodic porous media using an upscaling technique. The derivation is carried out in the time domain in the general situation where inertia may have a significant impact. 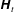The resulting model is non-local in time and involves two effective coefficients in the macroscopic filtration law, namely a dynamic apparent permeability tensor, $\unicode[STIX]{x1D643}_{t}$, and a vector, $\unicode[STIX]{x1D736}$, accounting for the time-decaying influence of the flow initial condition. This model generalizes previous non-local macroscale models restricted to creeping flow conditions. Ancillary closure problems are provided, which allow the effective coefficients to be computed. Symmetry and positiveness analyses of 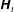$\unicode[STIX]{x1D643}_{t}$ are carried out, showing that this tensor is symmetric only in the creeping regime. The effective coefficients are functions of time, geometry, macroscopic forcings and the initial flow condition. This is illustrated through numerical solutions of the closure problems. Predictions are made on a simple periodic structure for a wide range of Reynolds numbers smaller than the critical value characterizing the first Hopf bifurcation. Finally, the performance of the macroscopic model for a variety of macroscopic forcings and initial conditions is examined in several case studies. Validation through comparisons with direct numerical simulations is performed. It is shown that the purely heuristic classical model, widely used for unsteady flow, consisting of a Darcy-like model complemented with an accumulation term on the filtration velocity, is inappropriate.

JFM classification

Mathematical Foundations: Mathematical Foundations Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 283 - 311
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abderahmane, K., Khalifa, O. A., Wahyudi, I. & Thomas, P. 2002 New extension of Darcy’s law to unsteady flows. Soils Found. 42, 53–63.Google Scholar
Achdou, Y. & Avellaneda, M. 1992 Influence of pore roughness and pore-size dispersion in estimating the permeability of a porous medium from electrical measurements. Phys. Fluids 4 (12), 2651–2673.Google Scholar
Agnaou, M., Lasseux, D. & Ahmadi, A. 2016 From steady to unsteady laminar flow in model porous structures: an investigation of the first Hopf bifurcation. Comput. Fluids 136, 67–82.Google Scholar
Allaire, G. 1992 Progress in Partial Differential Equations: Calculus of Variations, Applications. (Homogenization of the Unsteady Stokes Equations in Porous Media) , Longman Scientific and Technical.Google Scholar
Auriault, J. L. 1980 Dynamic behaviour of a porous medium saturated by a Newtonian fluid. Intl J. Engng Sci. 18 (6), 775–785.Google Scholar
Auriault, J. L. 1999 Comments on the paper ‘Local and global transitions to chaos and hysteresis in a porous layer heated from below’, by P. Vadasz. Trans. Porous Med. 37, 247–249.Google Scholar
Auriault, J. L., Borne, L. & Chambon, R. 1985 Dynamics of porous saturated media, checking of the generalized law of Darcy. J. Acoust. Soc. Am. 77 (5), 1641–1650.Google Scholar
Auriault, J. L., Boutin, C. & Geindreau, C. 2009 Homogenization of Coupled Phenomena in Heterogenous Media. ISTE.Google Scholar
Balhoff, M., Mikelić, A. & Wheeler, M. F. 2010 Polynomial filtration laws for low Reynolds number flows through porous media. Trans. Porous Med. 81 (1), 35–60.Google Scholar
Barrere, J., Gipouloux, O. & Whitaker, S. 1992 On the closure problem for Darcy’s law. Trans. Porous Med. 7 (3), 209–222.Google Scholar
Biot, M. A. 1956a Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 28 (2), 168–178.Google Scholar
Biot, M. A. 1956b Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 28 (2), 179–191.Google Scholar
Bories, S., Mojtabi, A., Prat, M. & Quintard, M. 2008 Transferts de chaleur dans les milieux poreux – conduction, convection, rayonnement. Tech. l’Ingt. BE 8250, 1–22.Google Scholar
Bourgeat, A., Marušić-Paloka, E. & Mikelić, A. 1996 Weak nonlinear corrections for Darcy’s law. Math. Models Meth. Appl. Sci. 06 (08), 1143–1155.Google Scholar
Breugem, W. P., Boersma, B. J. & Uittenbogaard, R. E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.Google Scholar
Burcharth, H. F. & Andersen, O. H. 1995 On the one-dimensional steady and unsteady porous flow equations. Coast. Engng 24, 233–257.Google Scholar
Chapman, A. M. & Higdon, J. J. L. 1992 Oscillatory Stokes flow in periodic porous media. Phys. Fluids A 4 (10), 2099–2116.Google Scholar
Charlaix, E., Kushnick, A. P. & Stokes, J. P. 1988 Experimental study of dynamic permeability in porous media. Phys. Rev. Lett. 61 (14), 1595–1598.Google Scholar
Cortis, A., Smeulders, D. M. J., Guermond, J. L. & Lafarge, D. 2003 Influence of pore roughness on high-frequency permeability. Phys. Fluids 15 (6), 1766–1775.Google Scholar
Corvaro, S., Mancinelli, A., Brocchini, M., Seta, E. & Lorenzoni, C. 2010 On the wave damping due to a permeable seabed. Coast. Engng 57, 1029–1041.Google Scholar
Cushman, J. H., Bennethum, L. S. & Hu, B. X. 2002 A primer on upscaling tools for porous media. Adv. Water Resour. 25 (8–12), 1043–1067.Google Scholar
Dogru, A. H., Alexander, W. & Panton, R. L. 1978 Numerical solution of unsteady flow problems in porous media by spline functions. J. Hydrol. 38, 179–195.Google Scholar
Gray, W. G. 1975 A derivation of the equations for multiphase transport. Chem. Engng Sci. 30, 229–233.Google Scholar
Gray, W. G. & Miller, C. T. 2014 Introduction to the Thermodynamically Constrained Averaging Theory for Porous Medium Systems. Springer.Google Scholar
Hall, K. R., Smith, G. M. & Turcke, D. J. 1995 Comparison of oscillatory and stationary flow through porous media. Coast. Engng 24, 217–232.Google Scholar
Hill, A. A. & Straughan, B. 2008 Poiseuille flow in a fluid overlying a porous medium. J. Fluid Mech. 603, 137–149.Google Scholar
Hill, A. A. & Straughan, B. 2009 Poiseuille flow in a fluid overlying a highly porous material. Adv. Water Resour. 32, 1609–1614.Google Scholar
Howes, F. A. & Whitaker, S. 1985 The spatial averaging theorem revisited. Chem. Engng Sci. 40, 1387–1392.Google Scholar
Jin, Y. & Kuznetsov, A. V. 2017 Turbulence modeling for flows in wall bounded porous media: an analysis based on direct numerical simulations. Phys. Fluids 29 (4), 045102.Google Scholar
Johnson, D. L. 1989 Scaling function for dynamic permeability in porous media. Phys. Rev. Lett. 63 (5), 580.Google Scholar
Johnson, D. L., Koplik, J. & Dashen, R. 1987 Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J. Fluid Mech. 176, 379–402.Google Scholar
Kuznetsov, A. V. & Nield, D. A. 2006 Forced convection with laminar pulsating flow in a saturated porous channel or tube. Trans. Porous Med. 65, 505–523.Google Scholar
Lasseux, D., Abbasian-Arani, A. A. & Ahmadi, A. 2011 On the stationary macroscopic inertial effects for one phase flow in ordered and disordered porous media. Phys. Fluids 23, 073103.Google Scholar
Lasseux, D. & Valdés-Parada, F. J. 2017 Symmetry properties of macroscopic transport coefficients in porous media. Phys. Fluids 29, 043303.Google Scholar
Laushey, L. M. & Popat, L. V. 1968 Darcy’s law during unsteady flow. In Ground Water: General Assembly of Bern (ed. Tison, L. J.), pp. 284–299. International Union of Geodesy and Geophysics (IUGG) and International Association of Scientific Hydrology (IASH), Boulder; http://iahs.info/redbooks/a077/077028.pdf.Google Scholar
Lévy, T. 1979 Propagation of waves in a fluid-saturated porous elastic solid. Intl J. Engng Sci. 17 (9), 1005–1014.Google Scholar
Lions, J. L. 1981 Some Methods in the Mathematical Analysis of Systems and Their Control. Gordon and Breach.Google Scholar
Lions, P. L. & Masmoudi, N. 2005 Homogenization of the Euler system in a 2D porous medium. J. Math. Pures Appl. 84, 1–20.Google Scholar
Marušić-Paloka, E. & Mikelić, A. 2000 The derivation of a nonlinear filtration law including the inertia effects via homogenization. Nonlinear Anal. Theory Meth. Applics. 42 (1), 97–137.Google Scholar
Masmoudi, N. 1998 The Euler limit of the Navier–Stokes equations, and rotating fluids with boundary. Arch. Rat. Mech. Anal. 142, 375–394.Google Scholar
Masmoudi, N. 2002 Homogenization of the compressible Navier–Stokes equations in a porous medium. ESAIM: Control Optim. Calc. Var. 8, 885–906.Google Scholar
Mei, C. C. & Vernescu, B. 2010 Homogenization Methods for Multiscale Mechanics. World Scientific.Google Scholar
Mikelić, A. 1994 Mathematical derivation of the Darcy-type law with memory effects, governing transient flow through porous medium. Glas. Mat. 29 (49), 57–77.Google Scholar
Nield, D. A. & Bejan, A. 2013 Convection in Porous Media. Springer.Google Scholar
Polubarinova-Kochina, P. Ya. 1962 Theory of Ground Water Movement (Translated from the Russian edition by J. M. Roger de Wiest). Princeton University Press.Google Scholar
Rajagopal, K. R. 2007 On a hierarchy of approximate models for flows of incompressible fluids through porous solids. Math. Models Meth. Appl. Sci. 17, 215–252.Google Scholar
Sahimi, M. 2011 Flow and Transport in Porous Media and Fractured Rock. From Classical Methods to Modern Approaches. Wiley.Google Scholar
Sanchez-Palencia, E. 1980 Non-Homogeneous Media and Vibration Theory, Lecture Notes in Physics. Springer.Google Scholar
Sheng, P. & Zhou, M.-Y. 1988 Dynamic permeability in porous media. Phys. Rev. Lett. 61 (14), 1591–1594.Google Scholar
Slattery, J. C. 1999 Advanced Transport Phenomena. Cambridge University Press.Google Scholar
Smeulders, D. M. J., Eggels, R. L. G. M. & Van Dongen, M. E. H. 1992 Dynamic permeability: reformulation of theory and new experimental and numerical data. J. Fluid Mech. 245, 211–227.Google Scholar
Sollitt, C. K. & Cross, R. H. 1972 Wave transmission through permeable breakwaters. In Proceedings of 13th Coastal Engineering Conference, ASCE, vol. 3, pp. 1827–1846. ASCE.Google Scholar
Teng, H. & Zhao, T. S. 2000 An extension of Darcy’s law to non-Stokes flow in porous media. Chem. Engng Sci. 55, 2737–2755.Google Scholar
Tilton, N. & Cortelezzi, L. 2008 Linear stability analysis of pressure-driven flows in channels with porous walls. J. Fluid Mech. 604, 411–445.Google Scholar
Truesdell, C. & Toupin, R. 1960 The Classical Field Theories. Springer.Google Scholar
Vadasz, P. 1999 Local and global transitions to chaos and hysteresis in a porous layer heated from below. Trans. Porous Med. 37, 213–235.Google Scholar
Whitaker, S. 1996 The Forchheimer equation: a theoretical development. Trans. Porous Med. 25, 27–61.Google Scholar
Whitaker, S. 1999 The Method of Volume Averaging. Kluwer.Google Scholar
Wood, B. D. & Valdés-Parada, F. J. 2013 Volume averaging: local and nonlocal closures using a Green’s function approach. Adv. Water Resour. 51, 139–167.Google Scholar
Zhou, M.-Y. & Sheng, P. 1989 First-principles calculations of dynamic permeability in porous media. Phys. Rev. B 39 (16), 12027–12039.Google Scholar
Zhu, T., Waluga, C., Wohlmuth, B. & Manhart, M. 2014 A study of the time constant in unsteady porous media flow using direct numerical simulation. Trans. Porous Med. 104, 161–179.Google Scholar