Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T17:23:48.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Mach-number scaling of individual azimuthal modes of subsonic co-flowing jets

Published online by Cambridge University Press:  14 March 2016

R. D. Sandberg  and
B. J. Tester
R. D. Sandberg*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
B. J. Tester
Affiliation:
Institute of Sound and Vibration Research, University of Southampton, Southampton SO17 1BJ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Mach-number scaling of the individual azimuthal modes of jet mixing noise was studied for jets in flight conditions, i.e. with co-flow. The data were obtained via a series of direct numerical simulations (DNS), performed of fully turbulent jets with a target Reynolds number, based on nozzle diameter, of 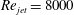$Re_{jet}=8000$. The DNS included a pipe 25 diameters in length in order to ensure that the flow developed to a fully turbulent state before exiting into a laminar co-flow, and to account for all possible noise generation mechanisms. To allow for a detailed study of the jet mixing noise component of the combined pipe–jet configuration, acoustic liner boundary conditions on the inside of the pipe and a modification to the synthetic turbulent inlet boundary condition of the pipe were applied to minimize internal noise in the pipe. Despite these measures, the use of a phased-array source breakdown technique was essential in order to isolate the sources associated with jet noise mechanisms from additional noise sources that could be attributed to internal noise or unsteady flow past the nozzle lip, in particular for the axisymmetric mode. Decomposing the sound radiation from the pipe–jet configuration into its azimuthal Fourier modes, and accounting for the co-flow effects, it was found that at 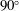$90^{\circ }$ the individual azimuthal Fourier modes of far-field pressure for the jet mixing noise component exhibit the same 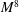$M^{8}$ scaling with the centreline jet Mach number as that experimentally documented for the overall noise field. Applying the phased-array source breakdown code to the DNS data at smaller angles to the jet axis, an increase of the velocity exponent of the jet noise source was found, approaching 10 at 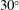$30^{\circ }$. At this smaller angle the higher azimuthal modes again showed the same behaviour as the axisymmetric mode.

JFM classification

Acoustics: Aeroacoustics Acoustics: Jet noise Wakes/Jets: Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 793 , 25 April 2016 , pp. 209 - 228
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bogey, C. & Bailly, C. 2010 Influence of nozzle-exit boundary-layer conditions on the flow and acoustic fields of initially laminar jets. J. Fluid Mech. 663, 507–538.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011 Large-eddy simulation of the flow and acoustic fields of a Reynolds number $10^{5}$ subsonic jet with tripped exit boundary layers. Phys. Fluids 23, 035104.Google Scholar
Cavalieri, A. V., Jordan, P., Colonius, T. & Gervais, Y. 2012 Axisymmetric superdirectivity in subsonic jets. J. Fluid Mech. 704, 388–420.Google Scholar
Crighton, D. G., Ffowcs Williams, J. E. & Cheeseman, L. C. 1977 The outlook for simulation of forward flight effects on aircraft noise. J. Aircraft 14 (11), 1117–1125.Google Scholar
Fisher, M., Harper-Bourne, M. & Glegg, S. A. L. 1977 Jet engine noise source location: the polar correlation technique. J. Sound Vib. 51 (1), 23–54.Google Scholar
Gutmark, E. & Ho, C. 1983 Preferred modes and the spreading rates of jets. Phys. Fluids 26, 2932.Google Scholar
Hussain, A. & Zedan, M. 1978 Effects of the initial condition on the axisymmetric free shear layer: effects of the initial momentum thickness. Phys. Fluids 21, 1100.Google Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1979 Filtered azimuthal correlations in the acoustic far field of a subsonic jet. AIAA J. 17 (1), 112–113.Google Scholar
Kennedy, C., Carpenter, M. & Lewis, R. 2000 Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Maths 35, 177–219.Google Scholar
Kennedy, C. & Gruber, A. 2008 Reduced aliasing formulations of the convective terms within the Navier–Stokes equations for a compressible fluid. J. Comput. Phys. 227, 1676–1700.Google Scholar
Kopiev, V., Chernyshev, S., Faranosov, G., Zaitsev, M. & Belyaev, I. 2010 Correlations of jet noise azimuthal components and their role in source identification. In 16th AIAA/CEAS Aeroacoustics Conference (31st AIAA Aeroacoustics Conference), Stockholm, Sweden; AIAA Paper 2010-4018.Google Scholar
Michalke, A. & Michel, U. 1979a Prediction of jet noise in flight from static tests. J. Sound Vib. 67 (3), 341–367.Google Scholar
Michalke, A. & Michel, U. 1979b Relation between static and in-flight directivities of jet noise. J. Sound Vib. 63, 602–605.Google Scholar
Olivetti, S., Sandberg, R. D. & Tester, B. J. 2015 Direct numerical simulation of turbulent flow with an impedance condition. J. Sound Vib. 344, 28.Google Scholar
Raman, G., Zaman, K. & Rice, E. 1989 Initial turbulence effect on jet evolution with and without tonal excitation. Phys. Fluids A 1, 1240.Google Scholar
Sandberg, R., Pichler, R., Chen, L., Johnstone, R. & Michelassi, V. 2015 Compressible direct numerical simulation of low-pressure turbines: Part I – Methodology. Trans. ASME J. Turbomach. 137, 051011.Google Scholar
Sandberg, R., Suponitsky, V. & Sandham, N. 2012 DNS of compressible pipe flow exiting into a coflow. Intl J. Heat Fluid Flow 35, 33–44.Google Scholar
Sandberg, R. D. 2011 An axis treatment for flow equations in cylindrical coordinates based on parity conditions. Comput. Fluids 49, 166–172.CrossRefGoogle Scholar
Sandberg, R. D. 2012 Numerical investigation of turbulent supersonic axisymmetric wakes. J. Fluid Mech. 702, 488–520.Google Scholar
Sandberg, R. D. 2014 DNS of turbulent round jets using acoustically lined canonical nozzles. In Proceedings of the AFMC, 19th Australasian Fluid Mechanics Conference, Melbourne, Australia; Paper 143.Google Scholar
Sandberg, R. D. & Sandham, N. D. 2006 Nonreflecting zonal characteristic boundary condition for direct numerical simulation of aerodynamic sound. AIAA J. 44 (2), 402–405.Google Scholar
Sandberg, R. D. & Tester, B. 2014 DNS of a turbulent jet issuing from an acoustically lined pipe. In Proceedings of the IUTAM Symposium on Advances in Computation, Modeling and Control of Transitional and Turbulent Flows.Google Scholar
Sandberg, R. D. & Tester, B. J. 2012 Application of a phased array technique to fully turbulent subsonic jet data obtained with DNS. In 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, Colorado; AIAA Paper 2012-2613.Google Scholar
Scalo, C., Bodart, J. & Lele, S. K. 2015 Compressible turbulent channel flow with impedance boundary conditions. Phys. Fluids 27, 035107.Google Scholar
Shur, M., Spalart, P. & Strelets, M. 2010 Reprint of: LES-based evaluation of a microjet noise reduction concept in static and flight conditions. Procedia IUTAM 1, 44–53.Google Scholar
Tam, C., Viswanathan, K., Ahuja, K. & Panda, J. 2008 The sources of jet noise: experimental evidence. J. Fluid Mech. 615, 253–292.Google Scholar
Tam, C. K. & Auriault, L. 1996 Time-domain impedance boundary conditions for computational aeroacoustics. AIAA J. 34 (5), 917–923.Google Scholar
Tanna, H. & Morris, P. 1977 In-flight simulation experiments on turbulent jet mixing noise. J. Sound Vib. 53 (3), 389–405.Google Scholar
Tester, B. J., Gabard, G. & Ricoup, T. 2012 Extracting engine noise source levels from phased array measurements with improved internal source models and evaluation against DNS-generated jet noise data. In 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, Colorado; AIAA Paper 2012-2272.Google Scholar
Tester, B. J. & Glegg, S. A. L. 2010 Phased array transformation methods to estimate non-compact jet noise source characteristics. In 16th AIAA/CEAS Aeroacoustics Conference (31st AIAA Aeroacoustics Conference), Stockholm, Sweden; AIAA Paper 2010-3739.Google Scholar
Tester, B. J. & Sandberg, R. D. 2013 Application of a phased array technique to DNS-generated turbulent subsonic jet data: source identification and comparison with an analytic model. In 19th AIAA/CEAS Aeroacoustics Conference (34th AIAA Aeroacoustics Conference), Berlin, Germany; AIAA Paper 2013-2235.Google Scholar
Touber, E. & Sandham, N. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.Google Scholar
Viswanathan, K. 2006 Scaling laws and a method for identifying components of jet noise. AIAA J. 44, 2274–2285.Google Scholar
White, F. M. 1991 Viscous Fluid Flow. McGraw-Hill.Google Scholar
Zaman, K. B. M. Q. 1985 Effect of initial condition on subsonic jet noise. AIAA J. 23, 1370–1373.Google Scholar