Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rosenberg, B. J.
Hultmark, M.
Vallikivi, M.
Bailey, S. C. C.
and
Smits, A. J.
2013.
Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 731,
Issue. ,
p.
46.
Hultmark, Marcus
Calaf, Marc
and
Parlange, Marc B.
2013.
A New Wall Shear Stress Model for Atmospheric Boundary Layer Simulations.
Journal of the Atmospheric Sciences,
Vol. 70,
Issue. 11,
p.
3460.
Deck, Sébastien
Renard, Nicolas
Laraufie, Romain
and
Weiss, Pierre-Élie
2014.
Large-scale contribution to mean wall shear stress in high-Reynolds-number flat-plate boundary layers up to 13650.
Journal of Fluid Mechanics,
Vol. 743,
Issue. ,
p.
202.
Stevens, Richard J. A. M.
Wilczek, Michael
and
Meneveau, Charles
2014.
Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
888.
Bailey, S. C. C.
Vallikivi, M.
Hultmark, M.
and
Smits, A. J.
2014.
Estimating the value of von Kármán’s constant in turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 749,
Issue. ,
p.
79.
Vallikivi, Margit
and
Smits, Alexander J.
2014.
Fabrication and Characterization of a Novel Nanoscale Thermal Anemometry Probe.
Journal of Microelectromechanical Systems,
Vol. 23,
Issue. 4,
p.
899.
Auel, Christian
Albayrak, Ismail
and
Boes, Robert M.
2014.
Turbulence Characteristics in Supercritical Open Channel Flows: Effects of Froude Number and Aspect Ratio.
Journal of Hydraulic Engineering,
Vol. 140,
Issue. 4,
Chin, C.
Philip, J.
Klewicki, J.
Ooi, A.
and
Marusic, I.
2014.
Reynolds-number-dependent turbulent inertia and onset of log region in pipe flows.
Journal of Fluid Mechanics,
Vol. 757,
Issue. ,
p.
747.
Grossmann, Siegfried
Lohse, Detlef
and
Sun, Chao
2014.
Velocity profiles in strongly turbulent Taylor-Couette flow.
Physics of Fluids,
Vol. 26,
Issue. 2,
Miller, M. A.
Estejab, B.
and
Bailey, S. C. C.
2014.
Evaluation of hot-wire spatial filtering corrections for wall turbulence and correction for end-conduction effects.
Experiments in Fluids,
Vol. 55,
Issue. 5,
Naka, Yoshitsugu
Stanislas, Michel
Foucaut, Jean-Marc
Coudert, Sebastien
Laval, Jean-Philippe
and
Obi, Shinnosuke
2015.
Space–time pressure–velocity correlations in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 771,
Issue. ,
p.
624.
Vallikivi, M.
Hultmark, M.
and
Smits, A. J.
2015.
Turbulent boundary layer statistics at very high Reynolds number.
Journal of Fluid Mechanics,
Vol. 779,
Issue. ,
p.
371.
Vallikivi, M.
Ganapathisubramani, B.
and
Smits, A. J.
2015.
Spectral scaling in boundary layers and pipes at very high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 771,
Issue. ,
p.
303.
Fan, Y.
Arwatz, G.
Van Buren, T. W.
Hoffman, D. E.
and
Hultmark, M.
2015.
Nanoscale sensing devices for turbulence measurements.
Experiments in Fluids,
Vol. 56,
Issue. 7,
Mouri, Hideaki
2015.
Mathematical model for logarithmic scaling of velocity fluctuations in wall turbulence.
Physical Review E,
Vol. 92,
Issue. 6,
Lee, Myoungkyu
and
Moser, Robert D.
2015.
Direct numerical simulation of turbulent channel flow up to .
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
395.
Vassilicos, J. C.
Laval, J.-P.
Foucaut, J.-M.
and
Stanislas, M.
2015.
The streamwise turbulence intensity in the intermediate layer of turbulent pipe flow.
Journal of Fluid Mechanics,
Vol. 774,
Issue. ,
p.
324.
Borisenkov, Youry
Kholmyansky, Michael
Krylov, Slava
Liberzon, Alex
and
Tsinober, Arkady
2015.
Multiarray Micromachined Probe for Turbulence Measurements Assembled of Suspended Hot-Film Sensors.
Journal of Microelectromechanical Systems,
Vol. 24,
Issue. 5,
p.
1503.
WADA, Yuki
FURUICHI, Noriyuki
TERAO, Yoshiya
and
TSUJI, Yoshiyuki
2015.
The experimental study on the turbulent statistics in the outer layer in high Reynolds number turbulent pipe flow.
Transactions of the JSME (in Japanese),
Vol. 81,
Issue. 830,
p.
15-00362.
He, S.
and
Seddighi, M.
2015.
Transition of transient channel flow after a change in Reynolds number.
Journal of Fluid Mechanics,
Vol. 764,
Issue. ,
p.
395.
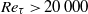 $R{e}_{\tau } \gt 20\hspace{0.167em} 000$, the streamwise Reynolds stress closely follows the scaling of the mean velocity profile, independent of the roughness, and over the same spatial extent. This observation extends the findings of a logarithmic law in the turbulence fluctuations as reported by Hultmark, Vallikivi & Smits (Phys. Rev. Lett., vol. 108, 2012) to include rough flows. The onset of the logarithmic region is found at a location where the wall distance is equal to ∼100 times the Kolmogorov length scale, which then marks sufficient scale separation for inertial scaling. Furthermore, in the logarithmic region the square root of the fourth-order moment also displays logarithmic behaviour, in accordance with the observation that the underlying probability density function is close to Gaussian in this region.
$R{e}_{\tau } \gt 20\hspace{0.167em} 000$, the streamwise Reynolds stress closely follows the scaling of the mean velocity profile, independent of the roughness, and over the same spatial extent. This observation extends the findings of a logarithmic law in the turbulence fluctuations as reported by Hultmark, Vallikivi & Smits (Phys. Rev. Lett., vol. 108, 2012) to include rough flows. The onset of the logarithmic region is found at a location where the wall distance is equal to ∼100 times the Kolmogorov length scale, which then marks sufficient scale separation for inertial scaling. Furthermore, in the logarithmic region the square root of the fourth-order moment also displays logarithmic behaviour, in accordance with the observation that the underlying probability density function is close to Gaussian in this region.

