Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-17T11:23:59.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Locomotion inside a surfactant-laden drop at low surface Péclet numbers

Published online by Cambridge University Press:  19 July 2018

Vaseem A. Shaik ,
Vishwa Vasani  and
Arezoo M. Ardekani Open the ORCID record for Arezoo M. Ardekani [Opens in a new window]
Vaseem A. Shaik
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907, USA
Vishwa Vasani
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907, USA
Arezoo M. Ardekani*
Affiliation:
School of Mechanical Engineering, Purdue University, West Lafayette, IN 47907, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

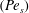We investigate the dynamics of a swimming microorganism inside a surfactant-laden drop for axisymmetric configurations under the assumptions of small Reynolds number and small surface Péclet number $(Pe_{s})$. Expanding the variables in 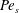$Pe_{s}$, we solve the Stokes equations for the concentric configuration using Lamb’s general solution, while the dynamic equation for the stream function is solved in the bipolar coordinates for the eccentric configurations. For a two-mode squirmer inside a drop, the surfactant redistribution can either increase or decrease the magnitude of swimmer and drop velocities, depending on the value of the eccentricity. This was explained by analysing the influence of surfactant redistribution on the thrust and drag forces acting on the swimmer and the drop. The far-field representation of a surfactant-covered drop enclosing a pusher swimmer at its centre is a puller; the strength of this far field is reduced due to the surfactant redistribution. The advection of surfactant on the drop surface leads to a time-averaged propulsion of the drop and the time-reversible swimmer that it engulfs, thereby causing them to escape from the constraints of the scallop theorem. We quantified the range of parameters for which an eccentrically stable configuration can be achieved for a two-mode squirmer inside a clean drop. The surfactant redistribution shifts this eccentrically stable position towards the top surface of the drop, although this shift is small.

JFM classification

Drops and Bubbles: Drops Biological Fluid Dynamics: Micro-organism dynamics Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 851 , 25 September 2018 , pp. 187 - 230
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berke, A. P., Turner, L., Berg, H. C. & Lauga, E. 2008 Hydrodynamic attraction of swimming microorganisms by surfaces. Phys. Rev. Lett. 101 (3), 038102.Google Scholar
Blake, J. R. 1971 A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 46 (1), 199–208.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16 (3–4), 242–251.Google Scholar
Brenner, H. & Leal, L. G. 1978 A micromechanical derivation of Fick’s law for interfacial diffusion of surfactant molecules. J. Colloid Interface Sci. 65 (2), 191–209.Google Scholar
Brenner, H. & Leal, L. G. 1982 Conservation and constitutive equations for adsorbed species undergoing surface diffusion and convection at a fluid–fluid interface. J. Colloid Interface Sci. 88 (1), 136–184.Google Scholar
Crowdy, D., Lee, S., Samson, O., Lauga, E. & Hosoi, A. E. 2011 A two-dimensional model of low-Reynolds number swimming beneath a free surface. J. Fluid Mech. 681, 24–47.Google Scholar
Datt, C., Zhu, L., Elfring, G. J. & Pak, O. S. 2015 Squirming through shear-thinning fluids. J. Fluid Mech. 784, R1.Google Scholar
Desai, N., Shaik, V. A. & Ardekani, A. M. 2018 Hydrodynamics-mediated trapping of micro-swimmers near drops. Soft Matt. 14 (2), 264–278.Google Scholar
Di Leonardo, R., Dell’Arciprete, D., Angelani, L. & Iebba, V. 2011 Swimming with an image. Phys. Rev. Lett. 106 (3), 038101.Google Scholar
Ding, Y., Qiu, F., Casadevall i Solvas, X., Chiu, F. W. Y., Nelson, B. J. & Demello, A. 2016 Microfluidic-based droplet and cell manipulations using artificial bacterial flagella. Micromachines 7 (2), 25.Google Scholar
Doostmohammadi, A., Stocker, R. & Ardekani, A. M. 2012 Low-Reynolds-number swimming at pycnoclines. Proc. Natl Acad. Sci. USA 109 (10), 3856–3861.Google Scholar
Elgeti, J. & Gompper, G. 2009 Self-propelled rods near surfaces. Europhys. Lett. 85 (3), 38002.Google Scholar
Elgeti, J., Winkler, R. G. & Gompper, G. 2015 Physics of microswimmers single particle motion and collective behavior: a review. Rep. Prog. Phys. 78 (5), 056601.Google Scholar
Fischer, T. M. 2004 Comment on shear viscosity of Langmuir monolayers in the low-density limit. Phys. Rev. Lett. 92 (13), 139603.Google Scholar
Gagnon, D. A., Keim, N. C., Shen, X. & Arratia, P. E. 2014 Fluid-induced propulsion of rigid particles in wormlike micellar solutions. Phys. Fluids 26 (10), 103101.Google Scholar
Haber, S. & Hetsroni, G. 1972 Hydrodynamics of a drop submerged in an unbounded arbitrary velocity field in the presence of surfactants. Appl. Sci. Res. 25 (1), 215–233.Google Scholar
Haj-Hariri, H., Nadim, A. & Borhan, A. 1993 Recriprocal theorem for concentric compound drops in arbitrary Stokes flows. J. Fluid Mech. 252 (1), 265–277.Google Scholar
Hanna, J. A. & Vlahovska, P. M. 2010 Surfactant-induced migration of a spherical drop in Stokes flow. Phys. Fluids 22 (1), 013102.Google Scholar
Happel, J. & Brenner, H. 1983 Low Reynolds Number Hydrodynamics. Martinus Nijhof.Google Scholar
Ishikawa, T., Simmonds, M. P. & Pedley, T. J. 2006 Hydrodynamic interaction of two swimming model micro-organisms. J. Fluid Mech. 568, 119–160.Google Scholar
Katz, D. F. 1974 On the propulsion of micro-organisms near solid boundaries. J. Fluid Mech. 64 (1), 33–49.Google Scholar
Lauga, E. 2011 Life around the scallop theorem. Soft Matt. 7 (7), 3060–3065.Google Scholar
Lauga, E., DiLuzio, W. R., Whitesides, G. M. & Stone, H. A. 2006 Swimming in circles: motion of bacteria near solid boundaries. Biophys. J. 90 (2), 400–412.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.Google Scholar
Leal, L. G. 1980 Particle motions in a viscous fluid. Annu. Rev. Fluid Mech. 12 (1), 435–476.Google Scholar
Leal, L. G. 2007 Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes. Cambridge University Press.Google Scholar
Lee, S., Bush, J. W. M., Hosoi, A. E. & Lauga, E. 2008 Crawling beneath the free surface: water snail locomotion. Phys. Fluids 20 (8), 082106.Google Scholar
Li, G. & Tang, J. X. 2009 Accumulation of microswimmers near a surface mediated by collision and rotational Brownian motion. Phys. Rev. Lett. 103 (7), 078101.Google Scholar
Li, G. J., Karimi, A. & Ardekani, A. M. 2014 Effect of solid boundaries on swimming dynamics of microorganisms in a viscoelastic fluid. Rheol. Acta 53 (12), 911–926.Google Scholar
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.Google Scholar
Lopez, D. & Lauga, E. 2014 Dynamics of swimming bacteria at complex interfaces. Phys. Fluids 26 (7), 071902.Google Scholar
Mandal, S., Ghosh, U. & Chakraborty, S. 2016 Effect of surfactant on motion and deformation of compound droplets in arbitrary unbounded Stokes flows. J. Fluid Mech. 803, 200–249.Google Scholar
Montenegro-Johnson, T. D., Smith, D. J. & Loghin, D. 2013 Physics of rheologically enhanced propulsion: different strokes in generalized Stokes. Phys. Fluids 25 (8), 081903.Google Scholar
Pak, O. S., Feng, J. & Stone, H. A. 2014 Viscous Marangoni migration of a drop in a Poiseuille flow at low surface Péclet numbers. J. Fluid Mech. 753, 535–552.Google Scholar
Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45 (1), 3–11.Google Scholar
Ramirez, J. A. & Davis, R. H. 1999 Mass transfer to a surfactant-covered bubble or drop. AIChE J. 45 (6), 1355–1358.Google Scholar
Reigh, S. Y., Zhu, L., Gallaire, F. & Lauga, E. 2017 Swimming with a cage: low-Reynolds-number locomotion inside a droplet. Soft Matt. 13 (17), 3161–3173.Google Scholar
Reynolds, A. J. 1965 The swimming of minute organisms. J. Fluid Mech. 23 (2), 241–260.Google Scholar
Rushton, E. & Davies, G. A. 1973 The slow unsteady settling of two fluid spheres along their line of centres. Appl. Sci. Res. 28 (1), 37–61.Google Scholar
Samaniuk, J. R. & Vermant, J. 2014 Micro and macrorheology at fluid–fluid interfaces. Soft Matt. 10 (36), 7023–7033.Google Scholar
Schwalbe, J. T., Phelan, F. R. Jr., Vlahovska, P. M. & Hudson, S. D. 2011 Interfacial effects on droplet dynamics in Poiseuille flow. Soft Matt. 7 (17), 7797–7804.Google Scholar
Shaik, V. A. & Ardekani, A. M. 2017a Motion of a model swimmer near a weakly deforming interface. J. Fluid Mech. 824, 42–73.Google Scholar
Shaik, V. A. & Ardekani, A. M. 2017b Point force singularities outside a drop covered with an incompressible surfactant: image systems and their applications. Phys. Rev. Fluids 2 (11), 113606.Google Scholar
Short, M. B., Solari, C. A., Ganguly, S., Powers, T. R., Kessler, J. O. & Goldstein, R. E. 2006 Flows driven by flagella of multicellular organisms enhance long-range molecular transport. Proc. Natl Acad. Sci. USA 103 (22), 8315–8319.Google Scholar
Sickert, M. & Rondelez, F. 2003 Shear viscosity of Langmuir monolayers in the low-density limit. Phys. Rev. Lett. 90 (12), 126104.Google Scholar
Sickert, M., Rondelez, F. & Stone, H. A. 2007 Single-particle Brownian dynamics for characterizing the rheology of fluid Langmuir monolayers. Europhys. Lett. 79 (6), 66005.Google Scholar
Spagnolie, S. E. & Lauga, E. 2012 Hydrodynamics of self-propulsion near a boundary: predictions and accuracy of far-field approximations. J. Fluid Mech. 700, 105–147.Google Scholar
Stimson, M. & Jeffery, G. B. 1926 The motion of two spheres in a viscous fluid. Proc. R. Soc. Lond. A 111 (757), 110–116.Google Scholar
Stone, H. A. 1990 A simple derivation of the time dependent convective diffusion equation for surfactant transport along a deforming interface. Phys. Fluids A 2 (1), 111–112.Google Scholar
Trouilloud, R., Yu, T. S., Hosoi, A. E. & Lauga, E. 2008 Soft swimming: exploiting deformable interfaces for low Reynolds number locomotion. Phys. Rev. Lett. 101 (4), 048102.Google Scholar
Whittaker, E. T. & Watson, G. N. 1996 A Course of Modern Analysis. Cambridge University Press.Google Scholar
Yazdi, S., Ardekani, A. M. & Borhan, A. 2015 Swimming dynamics near a wall in a weakly elastic fluid. J. Nonlinear Sci. 25 (5), 1153–1167.Google Scholar