Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-06-30T00:43:17.405Z Has data issue: false hasContentIssue false
  • English
  • Français

Localised continental shelf waves: geometric effects and resonant forcing

Published online by Cambridge University Press:  11 November 2015

J. T. Rodney  and
E. R. Johnson
J. T. Rodney*
Affiliation:
Tokio Millennium Re AG, UK Branch, 5th floor, 20 Fenchurch Street, LondonEC3M 3BY, UK
E. R. Johnson
Affiliation:
Department of Mathematics, University College London, Gower Street, LondonWC1E 6BT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Alongshore variations in coastline curvature or offshore depth profile can create localised regions of shelf-wave propagation with modes decaying outside these regions. These modes, termed localised continental shelf waves (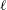$\ell$CSWs) here, exist only at certain discrete frequencies lying below the local maximum frequency, and above the far-field maximum frequency, for propagating shelf waves. The purpose of this paper is to obtain these frequencies and construct, both analytically and numerically, and discuss 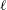$\ell$CSWs for shelves with arbitrary alongshore variations in offshore depth profile and coastline curvature. If the shelf curvature changes by a small fraction of its value over the shelf section of interest or an alongshore perturbation in offshore depth profile varies slowly over the same length scale then 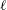$\ell$CSWs can be constructed using WKBJ theory. Two subcases are described: (i) if the propagating region is sufficiently long that the offshore structure of the 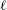$\ell$CSW varies appreciably alongshore then the frequency and alongshore structure are found from a sequence of local problems; (ii) if the propagating region is sufficiently short that the alongshore change in offshore structure of the 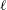$\ell$CSW is small then the alongshore modal structure is given in an explicit, uniformly valid form. A separate asymptotic theory is required for curvature perturbations to shelves that are otherwise straight rather than curved. Comparison with highly accurately numerically determined 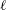$\ell$CSWs shows that both theories are extremely accurate, with the WKBJ theory having a significantly wider range of applicability. An idealised model for the generation of 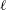$\ell$CSWs is also suggested. A localised time-periodic wind stress generates an evanescent continental shelf wave in the far field of a localised mode where the coast is almost straight and the response on the shelf is obtained numerically. If the forcing frequency is close to that of an 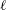$\ell$CSW then the wind stress excites energetic motions in the region of maximum curvature, creating a significant localised response possibly far from the forcing region.

JFM classification

Geophysical and Geological Flows: Shallow water flows Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 54 - 77
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamou, A. T. I., Craster, R. V. & Llewellyn Smith, S. G. 2007 Trapped edge waves in stratified rotating fluids: numerical and asymptotic results. J. Fluid Mech. 592, 195–220.Google Scholar
Adams, J. K. & Buchwald, V. T. 1969 The generation of continental shelf waves. J. Fluid Mech. 35, 815–826.CrossRefGoogle Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientist and Engineers, 2nd edn. McGraw-Hill.Google Scholar
Berry, M. V. & Mount, K. E. 1972 Semiclassical approximation in wave mechanics. Rep. Prog. Phys. 35, 315–397.Google Scholar
Biggs, N. R. T. 2012 Wave trapping in a two-dimensional sound-soft or sound-hard acoustic waveguide of slowly-varying width. Wave Motion 49 (1), 24–33.CrossRefGoogle Scholar
Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Bruno-Alfonso, A. & Latgé, A. 2008 Quantum rings of arbitrary shape and non-uniform width in a threading magnetic field. Phys. Rev. B 77 (20), 205303.Google Scholar
Buchwald, V. T. & Adams, J. K. 1968 Propagation of continental shelf waves. Proc. R. Soc. Lond. A 305, 235–250.Google Scholar
Gordon, R. L. & Huthnance, J. M. 1987 Storm-driven continental-shelf waves over the Scottish continental-shelf. Cont. Shelf Res. 7 (9), 1015–1048.Google Scholar
Gridin, D., Adamou, A. T. I. & Craster, R. V. 2004 Electronic eigenstates in quantum rings: Asymptotics and numerics. Phys. Rev. B 69, 155317.CrossRefGoogle Scholar
Gridin, D., Craster, R. V. & Adamou, A. T. I. 2005 Trapped modes in curved elastic plates. Proc. R. Soc. Lond. A 461, 1181–1197.Google Scholar
Grimshaw, R. H. 1977 Effects of a variable Coriolis parameter, coastline curvature and variable bottom topography on continental-shelf waves. J. Phys. Oceanogr. 7 (4), 547–554.2.0.CO;2>CrossRefGoogle Scholar
Heading, J. 1962 An Introduction to Phase Integral Methods. Methuen.Google Scholar
Heaps, N. S., Huthnance, J. M., Jones, J. E. & Wolf, J. 1988 Modeling of storm-driven shelf waves north of Scotland. 1. Idealized models. Cont. Shelf Res. 8, 1187–1210.Google Scholar
Huthnance, J. M. 1975 On trapped waves over a continental shelf. J. Fluid Mech. 69, 689–704.Google Scholar
Huthnance, J. M. 1978 On coastal trapped waves – analysis and numerical calculation by inverse iteration. J. Phys. Oceanogr. 8 (1), 74–92.2.0.CO;2>CrossRefGoogle Scholar
Huthnance, J. M. 1987 Effects of longshore shelf variations on barotropic continental-shelf waves, slope currents and ocean modes. Prog. Oceanogr. 19, 177–220.CrossRefGoogle Scholar
Johnson, E. R. 1989 Topographic waves in open domains. Part 1. Boundary conditions and frequency estimates. J. Fluid Mech. 200, 69–76.Google Scholar
Johnson, E. R. & Kaoullas, G. 2011 Bay-trapped low-frequency oscillations in lakes. Geophys. Astrophys. Fluid Dyn. 105 (1), 48–60.CrossRefGoogle Scholar
Johnson, E. R., Levitin, M. & Parnovski, P. 2006 Existence of eigenvalues of a linear operator pencil in a curved waveguide – localised shelf waves on a curved coast. SIAM J. Math. Anal. 32 (5), 1465–1481.Google Scholar
Johnson, E. R. & Rodney, J. T. 2011 Spectral methods for coastal trapped waves. Cont. Shelf Res. 31 (14), 1481–1489.CrossRefGoogle Scholar
Johnson, E. R., Rodney, J. T. & Kaoullas, G. 2012 Trapped modes in coastal waveguides. Wave Motion 49 (1), 212–216.Google Scholar
Kaoullas, G. & Johnson, E. R. 2010 Geographically localised shelf waves on curved coasts. Cont. Shelf Res. 30 (16), 1753–1760.CrossRefGoogle Scholar
Keller, J. B. 1958 Surface waves on water of non-uniform depth. J. Fluid Mech. 4 (6), 607–614.CrossRefGoogle Scholar
Nayfeh, A. H. 1993 Introduction to Perturbation Techniques. Wiley.Google Scholar
Neetu, S., Suresh, I., Shankar, R., Nagarajan, B., Sharma, R., Shenoi, S. S. C., Unnikrishnan, A. S. & Sundar, D. 2011 Trapped waves of the 27 November 1945 Makran tsunami: observations and numerical modeling. Nat. Hazards 59 (3), 1609–1618.Google Scholar
Postnova, J. & Craster, R. V. 2008 Trapped modes in elastic plates, ocean and quantum waveguides. Wave Motion 45, 565–579.Google Scholar
Rhines, P. B. 1969a Slow oscillations in an ocean of varying depth. Part 1. Abrupt topography. J. Fluid Mech. 37, 161–189.Google Scholar
Rhines, P. B. 1969b Slow oscillations in an ocean of varying depth. Part 2. Islands and seamounts. J. Fluid Mech. 37, 191–205.Google Scholar
Rodney, J. T. & Johnson, E. R. 2012 Localisation of coastal-trapped waves by lonshore variations in bottom topography. Continental Shelf Res. 32 (1), 130–137.Google Scholar
Rodney, J. T. & Johnson, E. R. 2014 Meanders and eddies from topographic transformation of coastal-trapped waves. J. Phys. Oceanography 44, 1133–1150.CrossRefGoogle Scholar
Schwing, F. B. 1989 Subtidal response of the Scotian Shelf bottom pressure field to meteorological forcing. Atmos.-Ocean 27, 157–180.Google Scholar
Shen, M. C., Meyer, R. E. & Keller, J. B. 1968 Spectra of water waves in channels and around islands. Phys. Fluids 11, 2289–2304.Google Scholar
Smith, R. 1970 The ray paths of topographic Rossby waves. Deep-Sea Res. 18, 477–483.Google Scholar
Smith, S. G. L. 2004 Stratified rotating edge waves. J. Fluid Mech. 498, 161–170.Google Scholar
Stocker, T. F. & Johnson, E. R. 1991 The trapping and scattering of topographic waves by estuaries and headlands. J. Fluid Mech. 222, 501–524.Google Scholar
Trefethen, L. N. 2000 Spectral Methods in MATLAB. SIAM.Google Scholar
Zhevandrov, P. 1991 Edge waves on a gently sloping beach – uniform asymptotics. J. Fluid Mech. 233, 483–493.Google Scholar