Article contents
A local model for the limiting configuration of interfacial solitary waves
Published online by Cambridge University Press: 25 June 2021
Abstract
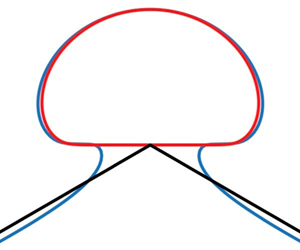
The limiting configuration of interfacial solitary waves between two homogeneous fluids consisting of a sharp  $120^{\circ }$ angle with an enclosed bubble of stagnant heavier fluid on top is investigated numerically. We use a boundary integral equation method to compute the almost limiting profiles which are nearly self-intersecting and thus extend the work of Pullin & Grimshaw (Phys. Fluids, vol. 31, 1988, pp. 3550–3559) by obtaining the overhanging solutions for very small density ratios. To further study the local configuration of the limiting profile, we propose a reduced model that replaces the
$120^{\circ }$ angle with an enclosed bubble of stagnant heavier fluid on top is investigated numerically. We use a boundary integral equation method to compute the almost limiting profiles which are nearly self-intersecting and thus extend the work of Pullin & Grimshaw (Phys. Fluids, vol. 31, 1988, pp. 3550–3559) by obtaining the overhanging solutions for very small density ratios. To further study the local configuration of the limiting profile, we propose a reduced model that replaces the  $120^{\circ }$ angle with two straight solid walls intersecting at the bottom of the bubble. Using a series truncation method, a one-parameter family of solutions depending on the angle between the two solid walls (denoted by
$120^{\circ }$ angle with two straight solid walls intersecting at the bottom of the bubble. Using a series truncation method, a one-parameter family of solutions depending on the angle between the two solid walls (denoted by  $\gamma$) is found. When
$\gamma$) is found. When  $\gamma = {2{\rm \pi} }/{3}$, it is shown that the simplified model agrees well with the near-limiting wave profile if the density ratio is small, and thus provides a good local approximation to the assumed limiting configuration. Interesting solutions for other values of
$\gamma = {2{\rm \pi} }/{3}$, it is shown that the simplified model agrees well with the near-limiting wave profile if the density ratio is small, and thus provides a good local approximation to the assumed limiting configuration. Interesting solutions for other values of  $\gamma$ are also explored.
$\gamma$ are also explored.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by



