Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-09T17:47:21.919Z Has data issue: false hasContentIssue false
  • English
  • Français

The local and global stability of confined planar wakes at intermediate Reynolds number

Published online by Cambridge University Press:  27 September 2011

M. P. Juniper ,
O. Tammisola  and
F. Lundell
M. P. Juniper*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
O. Tammisola
Affiliation:
Linné Flow Centre, KTH Mechanics, Royal Institute of Technology, S-100 44 Stockholm, Sweden
F. Lundell
Affiliation:
Linné Flow Centre, KTH Mechanics, Royal Institute of Technology, S-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

At high Reynolds numbers, wake flows become more globally unstable when they are confined within a duct or between two flat plates. At Reynolds numbers around 100, however, global analyses suggest that such flows become more stable when confined, while local analyses suggest that they become more unstable. The aim of this paper is to resolve this apparent contradiction by examining a set of obstacle-free wakes. 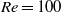In this theoretical and numerical study, we combine global and local stability analyses of planar wake flows at to determine the effect of confinement. We find that confinement acts in three ways: it modifies the length of the recirculation zone if one exists, it brings the boundary layers closer to the shear layers, and it can make the flow more locally absolutely unstable. Depending on the flow parameters, these effects work with or against each other to destabilize or stabilize the flow. In wake flows at 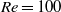with free-slip boundaries, flows are most globally unstable when the outer flows are 50 % wider than the half-width of the inner flow because the first and third effects work together. In wake flows at 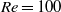with no-slip boundaries, confinement has little overall effect when the flows are weakly confined because the first two effects work against the third. Confinement has a strong stabilizing effect, however, when the flows are strongly confined because all three effects work together. By combining local and global analyses, we have been able to isolate these three effects and resolve the apparent contradictions in previous work.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Shear layers Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 218 - 238
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bearman, P. W. & Zdravkovich, M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89, 33–47.Google Scholar
2. Biancofiore, L., Gallaire, F. & Pasquetti, R. 2011 Influence of confinement on a two-dimensional wake. J. Fluid Mech. (submitted).Google Scholar
3. Chomaz, J.-M., Huerre, P. & Redekopp, L. 1991 A frequency selection criterion in spatially-developing flows. Stud. Appl. Maths 84, 119–144.Google Scholar
4. Cooper, A. J. & Crighton, D. G. 2000 Global modes and superdirective acoustic radiation in low-speed axisymmetrics jets. Eur. J. Mech. B 19, 559–574.CrossRefGoogle Scholar
5. Davis, R. W., Moore, E. F & Purtell, L. P. 1983 A numerical-experimental study of confined flow around rectangular cylinders. Phys. Fluids 27 (1), 46–59.Google Scholar
6. Fischer, P. F. 1997 An overlapping schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133, 84–101.Google Scholar
7. Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
8. Healey, J. J. 2007 Enhancing the absolute instability of a boundary layer by adding a far-away plate. J. Fluid Mech. 579, 29–61.CrossRefGoogle Scholar
9. Huerre, P. & Monkewitz, P. A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.Google Scholar
10. Huerre, P. & Monkewitz, P. A. 2000 Open shear flow instabilities. In Perspectives in Fluid Dynamics: a Collective Introduction to Current Research (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G. ). Cambridge University Press.Google Scholar
11. Hwang, R. R. & Yao, C.-C. 1997 A numerical study of vortex shedding from a square cylinder with ground effect. Trans. ASME: J. Fluids Engng 119, 512–518.Google Scholar
12. Juniper, M. P. 2006 The effect of confinement on the stability of planar shear flows. J. Fluid Mech. 565, 171–195.Google Scholar
13. Juniper, M. P. 2007 The full impulse response of two-dimensional shear flows and implications for confinement. J. Fluid Mech. 590, 163–185.Google Scholar
14. Juniper, M. P & Candel, S. M. 2003 The stability of ducted compound flows and consequences for the geometry of coaxial injectors. J. Fluid Mech. 482, 257–269.CrossRefGoogle Scholar
15. Kim, D.-H., Yang, K.-S. & Senda, M. 2004 Large eddy simulation of turbulent flow past a square cylinder confined in a channel. Comput. Fluids 33, 81–96.CrossRefGoogle Scholar
16. Lundell, F., Söderberg, L. D. & Alfredsson, P. H. 2011 Fluid mechanics of papermaking. Annu. Rev. Fluid Mech. 43, 195–217.Google Scholar
17. Monkewitz, P. A., Huerre, P. & Chomaz, J.-M. 1993 Global linear stability analysis of weakly non-parallel shear flows. J. Fluid Mech. 251, 1–20.CrossRefGoogle Scholar
18. Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.CrossRefGoogle Scholar
19. Rees, S. J. & Juniper, M. P. 2010 The effect of confinement on the stability of viscous planar jets and wakes. J. Fluid Mech. 656, 309–336.CrossRefGoogle Scholar
20. Richter, A. & Naudascher, E. 1976 Fluctuating forces on a rigid circular cylinder in confined flow. J. Fluid Mech. 78, 561–576.CrossRefGoogle Scholar
21. Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
22. Tammisola, O., Lundell, F., Schlatter, P., Wehrfritz, A. & Söderberg, L. D. 2011 Global linear and nonlinear stability of viscous confined plane wakes with co-flow. J. Fluid Mech. 675, 397–434.CrossRefGoogle Scholar