Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T00:22:31.376Z Has data issue: false hasContentIssue false
  • English
  • Français

Liquid jet primary breakup in a turbulent cross-airflow at low Weber number

Published online by Cambridge University Press:  01 October 2019

M. Broumand Open the ORCID record for M. Broumand [Opens in a new window] ,
M. Birouk  and
S. Vahid Mahmoodi J.
M. Broumand
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MB R3T 5V6, Canada
M. Birouk*
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MB R3T 5V6, Canada
S. Vahid Mahmoodi J.
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MB R3T 5V6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of turbulence characteristics of a cross-airflow including its velocity fluctuations and integral length and time scales on the primary breakup regime, trajectory and breakup height and time of a transversely injected liquid jet was investigated experimentally. Turbulence intensity of the incoming airflow was varied from 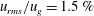$u_{rms}/u_{g}=1.5\,\%$ to 5.5 % (where 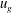$u_{g}$ is cross-airflow streamwise mean velocity and 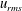$u_{rms}$ is the r.m.s. of the corresponding cross-airflow streamwise mean velocity fluctuation) by placing at the inlet of the test section a perforated plate/grid with a solidity ratio of 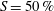$S=50\,\%$. Over the range of gas Weber number, 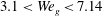$3.1<We_{g}<7.14$, the ensuing liquid jet exhibited more fluctuations and late breakup transitional behaviour under turbulent airflow conditions than in a uniform cross-airflow. Proper orthogonal decomposition of the liquid jet dynamics revealed that the use of grid caused a rise in the wavelength of travelling waves along the liquid jet, which hindered the transition of the liquid jet primary breakup regime from enhanced capillary breakup to the bag breakup mode. The quantitative results demonstrated that, at a constant airflow mean velocity, turbulent cross-airflow caused the liquid jet to bend earlier compared with its uniform counterpart. A power-law empirical correlation was proposed for the prediction of the liquid jet trajectory which takes into account the effect of turbulent Reynolds number. The liquid jet breakup height (in the 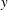$y$-axis direction) normalized by the jet diameter, and accordingly the liquid jet breakup time normalized by the airflow integral time scale, were found to decrease with increasing the airflow turbulence intensity. Two power-law empirical correlations were proposed to predict the liquid jet breakup height and time.

JFM classification

Turbulent Flows: Wave-turbulence interactions Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 775 - 792
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Mechanical and Industrial Engineering, University of Toronto, Toronto, ON M5S 3G8, Canada.

References

Ahn, K., Kim, J. & Yoon, Y. 2006 Effects of orifice internal flow on transverse injection into subsonic crossflows: cavitation and hydraulic flip. Atomiz. Sprays 16 (1), 15–34.Google Scholar
Amighi, A. & Ashgriz, N. 2019 Trajectory of a liquid jet in a high temperature and pressure gaseous cross flow. J. Engng Gas Turbines Power 141 (6), 061019.Google Scholar
Amini, G. 2018 Linear stability analysis of a liquid jet in a weak crossflow. Phys. Fluids 30 (8), 084105.Google Scholar
Arienti, M. & Soteriou, M. C. 2009 Time-resolved proper orthogonal decomposition of liquid jet dynamics. Phys. Fluids 21 (11), 112104.Google Scholar
Behzad, M., Ashgriz, N. & Mashayek, A. 2015 Azimuthal shear instability of a liquid jet injected into a gaseous cross-flow. J. Fluid Mech. 767, 146–172.Google Scholar
Birouk, M., Azzopardi, B. J. & Stäbler, T. 2003 Primary break-up of a viscous liquid jet in a cross airflow. Part. Part. Syst. Charact. 20 (4), 283–289.Google Scholar
Birouk, M., Iyogun, C. O. & Popplewell, N. 2007 Role of viscosity on trajectory of liquid jets in a cross-airflow. Atomiz. Sprays 17 (3), 267–287.Google Scholar
Broumand, M., Ahmed, M. MA. & Birouk, M. 2019 Experimental investigation of spray characteristics of a liquid jet in a turbulent subsonic gaseous crossflow. Proc. Combust. Inst. 37 (3), 3237–3244.Google Scholar
Broumand, M. & Birouk, M. 2015 A model for predicting the trajectory of a liquid jet in a subsonic gaseous crossflow. Atomiz. Sprays 25 (10), 871–893.Google Scholar
Broumand, M. & Birouk, M. 2016a Liquid jet in a subsonic gaseous crossflow: recent progress and remaining challenges. Prog. Energy Combust. Sci. 57, 1–29.Google Scholar
Broumand, M. & Birouk, M. 2016b Two-zone model for predicting the trajectory of liquid jet in gaseous crossflow. AIAA J. 54 (1), 1499–1511.Google Scholar
Broumand, M. & Birouk, M. 2017 Effect of nozzle-exit conditions on the near-field characteristics of a transverse liquid jet in a subsonic uniform cross airflow. Phys. Fluids 29 (11), 113303.Google Scholar
Brown, C. & McDonell, V. 2006 Near field behavior of a liquid jet in a crossflow. In Proceedings of the ILASS Americas 19th Annual Conference on Liquid Atomization and Spray Systems, pp. 1–9.Google Scholar
Brown, C. T., Mondragon, U. M. & McDonell, V. G. 2007 Investigation of the effect of injector discharge coefficient on penetration of a plain liquid jet into a subsonic crossflow. In 20th Annual Conference on Liquid Atomization and Spary Systems, Chicago, IL, May, pp. 15–18.Google Scholar
Charalampous, G. & Hardalupas, Y. 2014 Application of proper orthogonal decomposition to the morphological analysis of confined co-axial jets of immiscible liquids with comparable densities. Phys. Fluids 26 (11), 113301.10.1063/1.4900944Google Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Eggers, J. & Villermaux, E. 2008 Physics of liquid jets. Rep. Prog. Phys. 71 (3), 036601.Google Scholar
Eslamian, M., Amighi, A. & Ashgriz, N. 2014 Atomization of liquid jet in high-pressure and high-temperature subsonic crossflow. AIAA J. 52 (7), 1374–1385.Google Scholar
Farvardin, Johnson, M., Alaee, H., Martinez, A. & Dolatabadi, A. 2013 Comparative study of biodiesel and diesel jets in gaseous crossflow. J. Propul. Power 29 (6), 1292–1302.Google Scholar
Herrmann, M., Arienti, M. & Soteriou, M. 2011 The impact of density ratio on the liquid core dynamics of a turbulent liquid jet injected into a crossflow. J. Engng Gas Turbines Power 133 (6), 061501.Google Scholar
Holmes, P., Lumley, J. L., Berkooz, G. & Rowley, C. W. 2012 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Hsiang, L.-P. & Faeth, G. M. 1995 Drop deformation and breakup due to shock wave and steady disturbances. Intl J. Multiphase Flow 21 (4), 545–560.Google Scholar
Isaza, J. C., Salazar, R. & Warhaft, Z. 2014 On grid-generated turbulence in the near-and far field regions. J. Fluid Mech. 753, 402–426.10.1017/jfm.2014.375Google Scholar
Karagozian, A. R. 2010 Transverse jets and their control. Prog. Energy Combust. Sci. 36 (5), 531–553.Google Scholar
Kourmatzis, A. & Masri, A. R. 2015 Air-assisted atomization of liquid jets in varying levels of turbulence. J. Fluid Mech. 764, 95–132.Google Scholar
Krogstad, P.-Å. & Davidson, P. A. 2010 Is grid turbulence saffman turbulence? J. Fluid Mech. 642, 373–394.Google Scholar
Li, X., Gao, H. & Soteriou, M. C. 2017 Investigation of the impact of high liquid viscosity on jet atomization in crossflow via high-fidelity simulations. Phys. Fluids 29 (8), 082103.Google Scholar
Li, X. & Soteriou, M. C. 2016 High fidelity simulation and analysis of liquid jet atomization in a gaseous crossflow at intermediate weber numbers. Phys. Fluids 28 (8), 082101.Google Scholar
Li, X. & Soteriou, M. C. 2018 Detailed numerical simulation of liquid jet atomization in crossflow of increasing density. Intl J. Multiphase Flow 104, 214–232.Google Scholar
Liu, R. & Ting, D. S.-K. 2007 Turbulent flow downstream of a perforated plate: sharp-edged orifice versus finite-thickness holes. J. Fluids Engng 129 (9), 1164–1171.Google Scholar
Liu, R., Ting, D. S.-K. & Rankin, G. W. 2004 On the generation of turbulence with a perforated plate. Exp. Therm. Fluid Sci. 28 (4), 307–316.Google Scholar
Mazallon, J., Dai, Z. & Faeth, G. M. 1999 Primary breakup of nonturbulent round liquid jets in gas crossflows. Atomiz. Sprays 9 (3), 291–311.Google Scholar
Meyer, K. E., Pedersen, J. M. & Özcan, O. 2007 A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 583, 199–227.10.1017/S0022112007006143Google Scholar
Mohamed, M. S. & Larue, J. C. 1990 The decay power law in grid-generated turbulence. J. Fluid Mech. 219, 195–214.Google Scholar
Nobach, H., Tropea, C., Cordier, L., Bonnet, J.-P., Delville, J., Lewalle, J., Farge, M., Schneider, K. & Adrian, R. 2007 Review of some fundamentals of data processing. In Springer Handbook of Experimental Fluid Mechanics, pp. 1337–1398. Springer.Google Scholar
Osta, A. R. & Sallam, K. A. 2010 Nozzle-geometry effects on upwind-surface properties of turbulent liquid jets in gaseous crossflow. J. Propul. Power 26 (5), 936–946.Google Scholar
Pearson, K. 1901 LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinburgh Dublin Phil. Mag. J. Sci. 2 (11), 559–572.Google Scholar
Prakash, R. S., Sinha, A., Tomar, G. & Ravikrishna, R. V. 2018 Liquid jet in crossflow – effect of liquid entry conditions. Exp. Therm. Fluid Sci. 93, 45–56.Google Scholar
Rajamanickam, K. & Basu, S. 2017 Insights into the dynamics of spray–swirl interactions. J. Fluid Mech. 810, 82–126.10.1017/jfm.2016.710Google Scholar
Rana, S. & Herrmann, M. 2011 Primary atomization of a liquid jet in crossflow. Phys. Fluids 23 (9), 091109.Google Scholar
Sallam, K. A., Aalburg, C. & Faeth, G. M. 2004 Breakup of round nonturbulent liquid jets in gaseous crossflow. AIAA J. 42 (12), 2529–2540.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths. 45 (3), 561–571.Google Scholar
Thawley, S. M., Mondragon, U. M., Brown, C. T. & McDonell, V. G. 2008 Evaluation of column breakpoint and trajectory for a plain liquid jet injected into a crossflow. In Proceedings of the 21st Annual Conference on Liquid Atomization and Spray Systems, pp. 1–11.Google Scholar
Vich, G. & Ledoux, M. 1997 Investigation of a liquid jet in a subsonic cross-flow. Intl J. Fluid Mech. Res. 24 (1-3), 1–12.Google Scholar
Wang, M., Broumand, M. & Birouk, M. 2016 Liquid jet trajectory in a subsonic gaseous cross-flow: an analysis of published correlations. Atomiz. Sprays 26 (11), 1083–1110.Google Scholar
Wu, P.-K., Kirkendall, K. A., Fuller, R. P. & Nejad, A. S. 1997 Breakup processes of liquid jets in subsonic crossflows. J. Propul. Power 13 (1), 64–73.Google Scholar
Zheng, Y. & Marshall, A. W. 2011 Characterization of the initial spray from low-Weber-number jets in crossflow. Atomiz. Sprays 21 (7), 575–589.Google Scholar

Broumand et al. supplementary movie 1

Liquid jet in cross airflow-Case No 1

Download Broumand et al. supplementary movie 1(Video)
Video 4 MB

Broumand et al. supplementary movie 2

Liquid jet in cross airflow-Case No 4

Download Broumand et al. supplementary movie 2(Video)
Video 10 MB

Broumand et al. supplementary movie 3

Liquid jet in cross airflow-Case No 2

Download Broumand et al. supplementary movie 3(Video)
Video 4.1 MB