Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-05T03:17:09.896Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of the steady flow past rectangular cylinders

Published online by Cambridge University Press:  28 October 2021

A. Chiarini Open the ORCID record for A. Chiarini [Opens in a new window] ,
M. Quadrio Open the ORCID record for M. Quadrio [Opens in a new window]  and
F. Auteri Open the ORCID record for F. Auteri [Opens in a new window]
A. Chiarini
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
M. Quadrio
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
F. Auteri*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156Milano, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

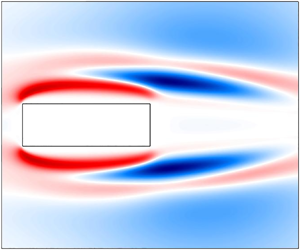
The primary instability of the flow past rectangular cylinders is studied to comprehensively describe the influence of the aspect ratio $AR$ and of rounding the leading- and/or trailing-edge corners. Aspect ratios ranging between $0.25$ and $30$ are considered. We show that the critical Reynolds number ($\textit {Re}_c$) corresponding to the primary instability increases with the aspect ratio, starting from $\textit {Re}_c \approx 34.8$ for $AR=0.25$ to a value of $\textit {Re}_c \approx 140$ for $AR = 30$. The unstable mode and its dependence on the aspect ratio are described. We find that positioning a small circular cylinder in the flow modifies the instability in a way strongly depending on the aspect ratio. The rounded corners affect the primary instability in a way that depends on both the aspect ratio and the curvature radius. For small $AR$, rounding the leading-edge corners has always a stabilising effect, whereas rounding the trailing-edge corners is destabilising, although for large curvature radii only. For intermediate $AR$, instead, rounding the leading-edge corners has a stabilising effect limited to small curvature radii only, while for $AR \geqslant 5$ it has always a destabilising effect. In contrast, for $AR \geqslant 2$ rounding the trailing-edge corners consistently increases $\textit {Re}_c$. Interestingly, when all the corners are rounded, the flow becomes more stable, at all aspect ratios. An explanation for the stabilising and destabilising effect of the rounded corners is provided.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Vortex streets Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 929 , 25 December 2021 , A36
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Almeida, O., Mansur, S.S. & Silveira-Neto, A. 2008 On the flow past rectangular cylinders: physical aspects and numerical simulation. Eng. Térmica 7 (1), 55–64.Google Scholar
Blackburn, H.M. & Lopez, J.M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15 (8), L57–L60.CrossRefGoogle Scholar
Blackburn, H.M., Marques, F. & Lopez, J.M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 522, 395–411.CrossRefGoogle Scholar
Blackburn, H.M. & Sheard, G.J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.CrossRefGoogle Scholar
Braza, M., Chassaing, P. & Ha Minh, H. 1986 Numerical study and physical analysis of the pressure and velocity fields in the near wake of a circular cylinder. J. Fluid Mech. 165, 79–130.CrossRefGoogle Scholar
Cao, Y. & Tamura, T. 2017 Supercritical flows past a square cylinder with rounded corners. Phys. Fluids 29 (8), 085110.CrossRefGoogle Scholar
Choi, C.-B. & Yang, K.-S. 2014 Three-dimensional instability in flow past a rectangular cylinder ranging from a normal flat plate to a square cylinder. Phys. Fluids 26 (6), 061702.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flowa: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.CrossRefGoogle Scholar
Cimarelli, A., Franciolini, M. & Crivellini, A. 2020 Numerical experiments in separating and reattaching flows. Phys. Fluids 32 (9), 095119.CrossRefGoogle Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Hammond, D.A. & Redekopp, L.G. 1997 Global dynamics of symmetric and asymmetric wakes. J. Fluid Mech. 331, 231–260.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem$++$. J. Numer. Maths 20 (3–4), 251–266.Google Scholar
Hourigan, K., Mills, R., Thompson, M.C., Sheridan, J., Dilin, P. & Welsh, M.C. 1993 Base pressure coefficients for flows around rectangular plates. J. Wind Engng Ind. Aerodyn. 49 (1), 311–318.CrossRefGoogle Scholar
Hourigan, K., Thompson, M.C. & Tan, B.T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15 (3), 387–398.CrossRefGoogle Scholar
Jackson, C.P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2018 Hydrodynamic characteristics of flow past a square cylinder at moderate Reynolds numbers. Phys. Fluids 30 (10), 104107.CrossRefGoogle Scholar
Kumar, B. & Mittal, S. 2006 Prediction of the critical Reynolds number for flow past a circular cylinder. Comput. Meth. Appl. Mech. Engng 195 (44), 6046–6058.CrossRefGoogle Scholar
Lamballais, E., Silvestrini, J. & Laizet, S. 2008 Direct numerical simulation of a separation bubble on a rounded finite-width leading edge. Intl J. Heat Fluid Flow 29, 612–625.CrossRefGoogle Scholar
Lamballais, E., Silvestrini, J. & Laizet, S. 2010 Direct numerical simulation of flow separation behind a rounded leading edge: study of curvature effects. Intl J. Heat Fluid Flow 31, 295–306.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2002 Response of base suction and vortex shedding from rectangular prisms to transverse forcing. J. Fluid Mech. 461, 25–49.CrossRefGoogle Scholar
Mills, R., Sheridan, J. & Hourigan, K. 2003 Particle image velocimetry and visualization of natural and forced flow around rectangular cylinders. J. Fluid Mech. 478, 299–323.CrossRefGoogle Scholar
Mittal, S. & Raghuvanshi, A. 2001 Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Intl J. Numer. Meth. Fluids 35 (4), 421–447.3.0.CO;2-M>CrossRefGoogle Scholar
Monkewitz, P.A., Huerre, P. & Chomaz, J.-M. 1993 Global linear stability analysis of weakly non-parallel shear flows. J. Fluid Mech. 251, 1–20.CrossRefGoogle Scholar
Morzyński, M., Afanasiev, K. & Thiele, F. 1999 Solution of the eigenvalue problems resulting from global non-parallel flow stability analysis. Comput. Meth. Appl. Mech. Engng 169 (1), 161–176.CrossRefGoogle Scholar
Nakamura, Y. & Nakashima, M. 1986 Vortex excitation of prisms with elongated rectangular, H and $\vdash$ cross-sections. J. Fluid Mech. 163, 149–169.CrossRefGoogle Scholar
Noack, B.R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Okajima, A. 1982 Strouhal numbers of rectangular cylinders. J. Fluid Mech. 123, 379–398.CrossRefGoogle Scholar
Ozono, S., Ohya, Y., Nakamura, Y. & Nakayama, R. 1992 Stepwise increase in the Strouhal number for flows around flat plates. Intl J. Numer. Meth. Fluids 15 (9), 1025–1036.CrossRefGoogle Scholar
Park, D. & Yang, K.-S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Pralits, J.O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Robichaux, J., Balachandar, S. & Vanka, S.P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.CrossRefGoogle Scholar
Rocchio, B., Mariotti, A. & Salvetti, M.V. 2020 Flow around a 5 : 1 rectangular cylinder: effects of upstream-edge rounding. J. Wind Engng Ind. Aerodyn. 204, 104237.CrossRefGoogle Scholar
Saad, Y. 2011 Numerical Methods for Large Eigenvalue Problems. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Saha, A.K., Muralidhar, K. & Biswas, G. 2000 Transition and chaos in two-dimensional flow past a square cylinder. J. Engng Mech. ASCE 126 (5), 523–532.CrossRefGoogle Scholar
Saiki, E.M. & Biringen, S. 1996 Numerical simulation of a cylinder in uniform flow: application of a virtual boundary method. J. Comput. Phys. 123 (2), 450–465.CrossRefGoogle Scholar
Schumm, M., Berger, E. & Monkewitz, P.A. 1994 Self-excited oscillations in the wake of two-dimensional bluff bodies and their control. J. Fluid Mech. 271, 17–53.CrossRefGoogle Scholar
Sheard, G.J., Fitzgerald, M.J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1998 Low-Reynolds-number flow around a square cylinder at incidence: study of blockage, onset of vortex shedding and outlet boundary condition. Intl J. Numer. Meth. Fluids 26 (1), 39–56.3.0.CO;2-P>CrossRefGoogle Scholar
Sohankar, A., Norberg, C. & Davidson, L. 1999 Simulation of three-dimensional flow around a square cylinder at moderate Reynolds numbers. Phys. Fluids 11 (2), 288–306.CrossRefGoogle Scholar
Sreenivasan, K.R., Strykowski, P.J. & Olinger, D.J. 1987 Hopf Bifurcation, Landau Equation, and Vortex Shedding Behind Circular Cylinders, pp. 1–33. American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FED.Google Scholar
Strykowski, P.J. & Sreenivasan, K.R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Tamura, T., Miyagi, T. & Kitagishi, T. 1998 Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Engng Ind. Aerodyn. 74, 531–542.CrossRefGoogle Scholar
Tan, B.T., Thompson, M. & Hourigan, K. 1998 Simulated flow around long rectangular plates under cross flow perturbations. Intl J. Fluid Dyn. 2, 1.Google Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Williamson, C.H.K., Gavrilakis, S., Machiels, L. & Monkewitz, P.A. 1996 Three-dimensional wake transition. In Advances in Turbulence VI Proceedings of the Sixth European Turbulence Conference, held in Lausanne, Switzerland, 2–5 July (ed. S. Gavrilakis, L. Machiels & P.A. Monkewitz), pp. 399–402. Springer.CrossRefGoogle Scholar
Williamson, C.H.K. & Govardhan, R. 2008 A brief review of recent results in vortex-induced vibrations. J. Wind Engng Ind. Aerodyn. 96 (6), 713–735.CrossRefGoogle Scholar
Yoon, D.-H., Yang, K.-S. & Choi, C.-B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22 (4), 043603.CrossRefGoogle Scholar
Zdravkovich, M.M. 1997 Flow Around Circular Cylinders. Oxford University Press.Google Scholar