Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T22:35:05.347Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear stability of Taylor–Couette flow of shear-thinning fluids: modal and non-modal approaches

Published online by Cambridge University Press:  13 July 2015

Y. Agbessi ,
B. Alibenyahia ,
C. Nouar ,
C. Lemaitre  and
L. Choplin
Y. Agbessi
Affiliation:
LRGP, UMR 7274 (CNRS), Université de Lorraine, 1 rue Grandville, BP 20451, 54001 Nancy CEDEX, France
B. Alibenyahia
Affiliation:
LApEH, Université Saad Dahlab, Blida, Algeria
C. Nouar*
Affiliation:
LEMTA, UMR 7563 (CNRS), Université de Lorraine, 2, avenue de la Forêt de Haye, TSA 60604,  54518 Vandoeuvre-L\`es-Nancy CEDEX, France
C. Lemaitre
Affiliation:
LRGP, UMR 7274 (CNRS), Université de Lorraine, 1 rue Grandville, BP 20451, 54001 Nancy CEDEX, France
L. Choplin
Affiliation:
LRGP, UMR 7274 (CNRS), Université de Lorraine, 1 rue Grandville, BP 20451, 54001 Nancy CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, the response of circular Couette flow of shear-thinning fluids between two infinitely long coaxial cylinders to weak disturbances is addressed. It is highlighted by transient growth analysis. Both power-law and Carreau models are used to describe the rheological behaviour of the fluid. The first part of the paper deals with the asymptotic long-time behaviour of three-dimensional infinitesimal perturbations. Using the normal-mode approach, an eigenvalue problem is derived and solved by means of the spectral collocation method. An extensive description and the classification of eigenspectra are presented. The influence of shear-thinning effects on the critical Reynolds numbers as well as on the critical azimuthal and axial wavenumbers is analysed. It is shown that with a reference viscosity defined with the characteristic scales 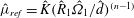$\hat{{\it\mu}}_{ref}=\hat{K}(\hat{R}_{1}\hat{{\it\Omega}}_{1}/\hat{d})^{(n-1)}$ for a power-law fluid and 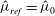$\hat{{\it\mu}}_{ref}=\hat{{\it\mu}}_{0}$ for a Carreau fluid, the shear-thinning character is destabilizing for counter-rotating cylinders. Moreover, the axial wavenumber increases with 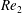$\mathit{Re}_{2}$ and with shear-thinning effects. The second part investigates the short-time behaviour of the disturbance using the non-modal approach. For the same inner and outer Reynolds numbers, the amplification of the kinetic energy perturbation becomes much more important with increasing shear-thinning effects. Two different mechanisms are used to explain the transient growth, depending on whether or not there is a stratification of the angular momentum. On the Rayleigh line and for Newtonian fluids, the optimal perturbation is in the form of azimuthal streaks, which transform into Taylor vortices through the anti-lift-up mechanism. In the other cases, the optimal perturbation is initially oriented against the base flow, then it tilts to align with the base flow at optimal time. The scaling laws for the optimal energy amplification proposed in the literature for Newtonian fluids are extended to shear-thinning fluids.

JFM classification

Instability: Instability Instability: Nonlinear instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 776 , 10 August 2015 , pp. 354 - 389
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alibenyahia, B., Lemaitre, C., Nouar, C. & Ait-Messaoudene, N. 2012 Revisiting the stability of circular Couette flow of shear-thinning fluids. J. Non-Newtonian Fluid Mech. 183, 37–51.CrossRefGoogle Scholar
Andereck, C. D., Liu, S. S. & Swinney, H. L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.Google Scholar
Ashrafi, N. & Khayat, R. E. 2000 Shear-induced chaos in Taylor-vortex flow. Phys. Rev. E 61, 1455–1467.Google Scholar
Bird, R., Amstrong, R. & Hassager, O. 1987 Dynamics of Polymeric Liquids. Wiley–Interscience.Google Scholar
Butler, K. M. & Farrell, B. M. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 1637–1650.Google Scholar
Carreau, J. P. 1972 Rheological equations from molecular network theories. J. Rheol. 16, 99–127.Google Scholar
Caton, F. 2006 Linear stability analysis of circular Couette flow of inelastic viscoplastic fluids. J. Non-Newtonian Fluid Mech. 134, 148–154.Google Scholar
Cherubini, S., Robinet, J.-C., Bottaro, A. & De Palma, P. 2010 Optimal wave packets in a boundary layer and initial phases of a turbulent spot. J. Fluid Mech. 656, 231–259.Google Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21, 385–425.Google Scholar
Coronado-Malutti, O., Mendes, P. R. S. & Carvallo, M. S. 1986 Instability of inelastic shear-thinning liquids in a Couette flow between concentric cylinders. Chem. Engng Sci. 41, 2915–2923.Google Scholar
DiPrima, R. C. & Hall, P. 1984 Complex eigenvalues for the stability of couette flow. Proc. R. Soc. Lond. A 396 (1810), 75–94.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability, Cambridge Mathematical Library. Cambridge University Press.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P. Y., Richard, D. & Zhan, J. P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17, 095103,1–19.CrossRefGoogle Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.Google Scholar
Escudier, M. P., Gouldson, I. W. & Jones, D. M. 1995 Taylor vortices in Newtonian and shear-thinning liquids. Proc. R. Soc. Lond. A 449, 155–176.Google Scholar
Gebhardt, T. & Grossmann, S. 1993 The Taylor–Couette eigenvalue problem with independently rotating cylinders. Z. Phys. B 90 (4), 475–490.Google Scholar
Giesekus, H. 1966 Zur Stabilität von Strömungen viskoelastischer Flüssigkeiten. 1. Ebene und kreisförmige Couette-Strömung. Rheol. Acta 5, 239–252.Google Scholar
Groisman, A. & Steinberg, V. 1998 Mechanism of elastic instability in Couette flow of polymer solutions: experiments. Phys. Fluids 10, 2451–2463.Google Scholar
Hristova, H., Roch, S., Schmid, P. & Tuckerman, S. L. 2002 Transient growth in Taylor–Couette flow. Phys. Fluids 14, 3475–3484.Google Scholar
Jastrzebski, M., Zaidani, H. A. & Wronski, S. 1992 Stability of Couette flow of liquids with power-law viscosity. Rheol. Acta 31, 264–273.CrossRefGoogle Scholar
Koschmieder, E. L. 1993 Bénard Cells and Taylor Vortices, Cambridge Monographs on Mechanics and Applied Mathematics. Cambridge University Press.Google Scholar
Krueger, E. R., Gross, A. & Diprima, R. C. 1966 On the relative importance of Taylor-vortex and non-axisymmetric modes in flow between rotating cylinders. J. Fluid Mech. 24, 521–538.CrossRefGoogle Scholar
Langford, F., Tagg, R., Kostelich, E., Swinney, H. L. & Glubitsky, M. 1988 Primary instabilities and bicriticality in flow between counter rotating cylinders. Phys. Fluids 31, 776–785.CrossRefGoogle Scholar
Larson, R. G., Shaqfeh, E. S. G. & Muller, S. J. 1990 A purely elastic instability in Taylor–Couette flow. J. Fluid Mech. 210, 573–600.Google Scholar
Liu, R. & Liu, Q. S. 2011 Non-modal instability in plane Couette flow of a power law fluid. J. Fluid Mech. 676, 145–171.Google Scholar
Liu, R. & Liu, Q. S. 2012 Non-modal stability in Hagen–Poiseuille flow of a shear-thinning fluid. Phys. Rev. E 85, 066318.CrossRefGoogle Scholar
Lockett, T. J., Richardson, S. M. & Worraker, W. J. 2004 The stability of inelastic non-Newtonian fluids in Couette flow between concentric cylinders. Trans. ASME J. Fluids Engng 126, 385–390.Google Scholar
Maretzke, S., Hof, B. & Avila, M. 2014 Transient growth in linearly stable Taylor–Couette flows. J. Fluid Mech. 742, 254–290.Google Scholar
Meseguer, A. 2002 Energy transient growth in the Taylor–Couette problem. Phys. Fluids 14, 1655–1660.Google Scholar
Monokrousos, A., Akervik, E., Brandt, L. & Henningson, D. S. 2010 Global three-dimensional optimal disturbances in the blasius boundary – layer flow using time-steppers. J. Fluid Mech. 650, 181–214.Google Scholar
Muller, S. J., Larson, R. G. & Shaqfeh, E. S. G. 1989 A purely elastic transition in Taylor–Couette flow. Rheol. Acta 24, 499–503.Google Scholar
Orr, W. M. ’F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Proc. R. Irish Acad. 27, 9–138.Google Scholar
Pascal, J. P. & Rasmussen, H. 1995 Stability of power law fluid flow between rotating cylinders. Dyn. Stab. Syst. 10, 65–93.Google Scholar
Ranganathan, B. T. & Govindarajan, R. 2001 Stabilization and destabilization of channel flow by location of viscosity – stratified fluid layer. Phys. Fluids 13, 1–3.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Shaqfeh, E. S. G., Muller, S. J. & Larson, R. G. 1992 The effect of gap width and dilute-solution properties on the viscoelastic Taylor–Couette instability. J. Fluid Mech. 235, 285–317.Google Scholar
Shu, F. H. 1982 The Physical Universe: An Introduction to Astronomy. University Science Books.Google Scholar
Sinevic, V., Kuboi, R. & Nienow, A. W. 1986 Power numbers, Taylor numbers and Taylor vortices in viscous Newtonian and non-Newtonian fluids. Chem. Engng Sci. 41, 2915–2923.Google Scholar
Snyder, H. A. 1968 Stability of a rotating Couette flow. I asymmetric waveform. Phys. Fluids 11, 728–734.Google Scholar
Tagg, R. 1994 The Couette–Taylor problem. Nonlinear Sci. Today 4, 1–25.Google Scholar
Tanner, R. 2000 Engineering Rheology. Oxford University Press.CrossRefGoogle Scholar
Taylor, G. I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Phil. Trans. R. Soc. Lond. A 223, 289–343.Google Scholar
Trefethen, L. N., Chapman, S. J. R., Henningson, D. S., Meseguer, A., Mullin, T. & Nieuwstadt, F. T. M.2000 Threshold amplitudes for transition to turbulence in a pipe. Numerical Analysis Report 00/17.Google Scholar
Van Atta, C. 1966 Exploratory measurements in spiral turbulence. J. Fluid Mech. 25, 495–512.Google Scholar
Vitoshkin, H., Heifetz, E., Gelfgat, A. Yu. & Harnik, N. 2012 On the role of vortex stretching in energy optimal growth of three-dimensional perturbations on plane parallel shear flows. J. Fluid Mech. 707, 369–380.Google Scholar