Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yang, Lisong
Kazmierski, Bethany K.
Hoath, Stephen D.
Jung, Sungjune
Hsiao, Wen-Kai
Wang, Yiwei
Berson, Arganthaël
Harlen, Oliver
Kapur, Nik
and
Bain, Colin D.
2014.
Determination of dynamic surface tension and viscosity of non-Newtonian fluids from drop oscillations.
Physics of Fluids,
Vol. 26,
Issue. 11,
Brenn, G.
and
Plohl, G.
2015.
The oscillating drop method for measuring the deformation retardation time of viscoelastic liquids.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 223,
Issue. ,
p.
88.
Hoath, Stephen D.
Hsiao, Wen-Kai
Martin, Graham D.
Jung, Sungjune
Butler, Simon A.
Morrison, Neil F.
Harlen, Oliver G.
Yang, Lisong S.
Bain, Colin D.
and
Hutchings, Ian M.
2015.
Oscillations of aqueous PEDOT:PSS fluid droplets and the properties of complex fluids in drop-on-demand inkjet printing.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 223,
Issue. ,
p.
28.
Liu, Zhong
Tan, Shan Wen
and
Brenn, G.
2015.
Numerical Study for Shape Oscillation of Free Viscoelastic Drop Using the Arbitrary Lagrangian-Eulerian Method.
Applied Mechanics and Materials,
Vol. 789-790,
Issue. ,
p.
316.
Tonini, S.
and
Cossali, G.E.
2016.
One-dimensional analytical approach to modelling evaporation and heating of deformed drops.
International Journal of Heat and Mass Transfer,
Vol. 97,
Issue. ,
p.
301.
Li, Fang
Yin, Xie-Yuan
and
Yin, Xie-Zhen
2017.
Oscillation of satellite droplets in an Oldroyd-B viscoelastic liquid jet.
Physical Review Fluids,
Vol. 2,
Issue. 1,
Brenn, Günter
2017.
Analytical Solutions for Transport Processes.
p.
123.
Raudino, Antonio
Raciti, Domenica
and
Corti, Mario
2017.
Anomalous Behavior of Ultra-Low-Amplitude Capillary Waves. A Glimpse of the Viscoelastic Properties of Interfacial Water?.
Langmuir,
Vol. 33,
Issue. 25,
p.
6439.
Staat, Hendrik J. J.
van der Bos, Arjan
van den Berg, Marc
Reinten, Hans
Wijshoff, Herman
Versluis, Michel
and
Lohse, Detlef
2017.
Ultrafast imaging method to measure surface tension and viscosity of inkjet-printed droplets in flight.
Experiments in Fluids,
Vol. 58,
Issue. 1,
Kremer, J.
Kilzer, A.
and
Petermann, M.
2018.
Simultaneous measurement of surface tension and viscosity using freely decaying oscillations of acoustically levitated droplets.
Review of Scientific Instruments,
Vol. 89,
Issue. 1,
Kremer, J.
Bürk, V.
Pollak, S.
Kilzer, A.
and
Petermann, M.
2018.
Viscosity of squalane under carbon dioxide pressure — Comparison of acoustic levitation with conventional methods.
The Journal of Supercritical Fluids,
Vol. 141,
Issue. ,
p.
252.
Li, Fang
Yin, Xie-Yuan
and
Yin, Xie-Zhen
2019.
Small-amplitude shape oscillation and linear instability of an electrically charged viscoelastic liquid droplet.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 264,
Issue. ,
p.
85.
Li, Fang
Ke, Shi-You
Yin, Xie-Yuan
and
Yin, Xie-Zhen
2019.
Effect of finite conductivity on the nonlinear behaviour of an electrically charged viscoelastic liquid jet.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
5.
Varma Raja Kochanattu, Gautham
Cossali, Gianpietro Elvio
and
Tonini, Simona
2020.
Droplet Interactions and Spray Processes.
Vol. 121,
Issue. ,
p.
3.
Tonini, S.
Varma RajaKochanattu, G.
and
Cossali, G.E.
2020.
The effect of evaporation on the oscillation frequency of an inviscid liquid drop.
International Communications in Heat and Mass Transfer,
Vol. 116,
Issue. ,
p.
104609.
Li, Fang
Yin, Xie-Yuan
and
Yin, Xie-Zhen
2020.
Shape oscillations of a viscoelastic droplet suspended in a viscoelastic host liquid.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Brenn, Günter
2020.
Droplet Interactions and Spray Processes.
Vol. 121,
Issue. ,
p.
239.
Wagoner, Brayden W.
Garg, Vishrut
Harris, Michael T.
Ramkrishna, Doraiswami
and
Basaran, Osman A.
2021.
Oscillations of a ring-constrained charged drop.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
Nikitin, Kirill
Vassilevski, Yuri
and
Yanbarisov, Ruslan
2021.
An implicit scheme for simulation of free surface non-Newtonian fluid flows on dynamically adapted grids.
Russian Journal of Numerical Analysis and Mathematical Modelling,
Vol. 36,
Issue. 3,
p.
165.
Zhou, Huan-Xiang
2021.
Shape recovery of deformed biomolecular droplets: Dependence on condensate viscoelasticity.
The Journal of Chemical Physics,
Vol. 155,
Issue. 14,
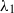 ${\lambda }_{1} $ and
${\lambda }_{1} $ and 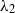 ${\lambda }_{2} $ involved in the viscoelastic material law. The aim of this study is to quantify the influences of the two time scales on the oscillation behaviour of the drop and to propose an experimental method to determine one of the time scales by measuring damped oscillations of a drop. A proof-of-concept experiment is presented to show the potential and limitations of the method. Results show that values of
${\lambda }_{2} $ involved in the viscoelastic material law. The aim of this study is to quantify the influences of the two time scales on the oscillation behaviour of the drop and to propose an experimental method to determine one of the time scales by measuring damped oscillations of a drop. A proof-of-concept experiment is presented to show the potential and limitations of the method. Results show that values of 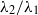 ${\lambda }_{2} / {\lambda }_{1} $ from these measurements are orders of magnitude smaller than typical values used in simulations of viscoelastic flows.
${\lambda }_{2} / {\lambda }_{1} $ from these measurements are orders of magnitude smaller than typical values used in simulations of viscoelastic flows.