Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T07:12:57.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear modelling of self-similar jet turbulence

Published online by Cambridge University Press:  25 May 2021

Phoebe Kuhn Open the ORCID record for Phoebe Kuhn [Opens in a new window] ,
Julio Soria Open the ORCID record for Julio Soria [Opens in a new window]  and
Kilian Oberleithner Open the ORCID record for Kilian Oberleithner [Opens in a new window]
Phoebe Kuhn*
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institute of Fluid Dynamics and Technical Acoustics, TU Berlin, 10623Berlin, Germany
Julio Soria
Affiliation:
Laboratory for Turbulence Research in Aerospace and Combustion, Department of Mechanical and Aerospace Engineering, Monash University Melbourne, Clayton, VIC 3800, Australia
Kilian Oberleithner
Affiliation:
Laboratory for Flow Instabilities and Dynamics, Institute of Fluid Dynamics and Technical Acoustics, TU Berlin, 10623Berlin, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

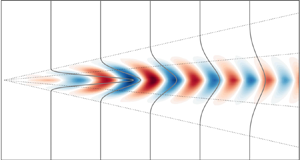
Coherent structures in the far field of a round turbulent jet are investigated experimentally and modelled by local linear stability analysis (LSA) and local resolvent analysis (RA). The study aims to determine the potential and limitations of mean flow-based linear models predicting the far field dynamics. Particular emphasis is placed on the high wavenumber and frequency range. The study is based on time-resolved stereoscopic particle image velocimetry (PIV) data acquired in the self-similar region of the jet. Spectral proper orthogonal decomposition (SPOD) is applied to the dataset to identify empirical coherent structures with azimuthal wavenumbers ranging from $m=0$ to $m=\pm 5$. The leading SPOD mode features low-rank behaviour over a wide frequency range and is found to account for the major part of total turbulent production. Thus, the leading SPOD mode captures the anisotropic part of turbulence, which is still significant even at the highest resolved frequencies reaching into the inertial subrange. The LSA determines stable but discrete eigenmodes that are excellently in line with the SPOD modes. This applies especially to modes at mid-range to high frequencies and higher azimuthal wavenumbers where the LSA predicts strongly decaying modes. Moreover, the RA modes are in very good agreement with LSA and SPOD modes, indicating a predominantly resonant mechanism. The present study shows that an unexpectedly wide range of turbulent scales in the self-similar region of the jet can be reproduced based on linearized mean-field models.

JFM classification

Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 919 , 25 July 2021 , A7
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abdel-Rahman, A. 2010 A review of effects of initial and boundary conditions on turbulent jets. WSEAS Trans. Fluid Mech. 5 (4), 257–275.Google Scholar
Atkinson, C., Buchmann, N.A., Amili, O. & Soria, J. 2014 On the appropriate filtering of PIV measurements of turbulent shear flows. Exp. Fluids 55 (1), 1654.CrossRefGoogle Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.CrossRefGoogle Scholar
Burattini, P., Antonia, R.A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.CrossRefGoogle Scholar
Cater, J.E. & Soria, J. 2002 The evolution of round zero-net-mass-flux jets. J. Fluid Mech. 472, 167–200.CrossRefGoogle Scholar
Cavalieri, A.V.G., Jordan, P. & Lesshafft, L. 2019 Wave-packet models for jet dynamics and sound radiation. Appl. Mech. Rev. 71 (2), 020802.CrossRefGoogle Scholar
Cavalieri, A.V.G., Rodríguez, D., Jordan, P., Colonius, T. & Gervais, Y. 2013 Wavepackets in the velocity field of turbulent jets. J. Fluid Mech. 730, 559–592.CrossRefGoogle Scholar
Crouch, J.D., Garbaruk, A. & Magidov, D. 2007 Predicting the onset of flow unsteadiness based on global instability. J. Comput. Phys. 224 (2), 924–940.CrossRefGoogle Scholar
Ewing, D., Frohnapfel, B., George, W.K., Pedersen, J.M. & Westerweel, J. 2007 Two-point similarity in the round jet. J. Fluid Mech. 577, 309–330.CrossRefGoogle Scholar
Gamard, S., George, W.K., Jung, D. & Woodward, S. 2002 Application of a ‘slice’ proper orthogonal decomposition to the far field of an axisymmetric turbulent jet. Phys. Fluids 14 (7), 2515–2522.CrossRefGoogle Scholar
Gamard, S., Jung, D. & George, W.K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 2. The far-field region. J. Fluid Mech. 514, 205–230.CrossRefGoogle Scholar
George, W.K. 2012 Asymptotic effect of initial and upstream conditions on turbulence. J. Fluids Engng 134 (6), 061203.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.CrossRefGoogle Scholar
Hodžić, A. 2018 A tensor calculus formulation of the lumley decomposition applied to the turbulent axi-symmetric jet far-field. Phd thesis, Technical University of Denmark.Google Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22, 473–537.CrossRefGoogle Scholar
Jordan, P., Zhang, M., Lehnasch, G. & Cavalieri, A.V. 2017 Modal and non-modal linear wavepacket dynamics in turbulent jets. In 23rd AIAA/CEAS Aeroacoustics Conference, pp. 1–18. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Jung, D., Gamard, S. & George, W.K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 1. The near-field region. J. Fluid Mech. 514, 173–204.CrossRefGoogle Scholar
Kaiser, T.L., Lesshafft, L. & Oberleithner, K. 2019 Prediction of the flow response of a turbulent flame to acoustic pertubations based on mean flow resolvent analysis. Trans. ASME J. Engng Gas Turbines Power 141 (11), 111021.CrossRefGoogle Scholar
Karami, S. & Soria, J. 2018 Analysis of coherent structures in an under-expanded supersonic impinging jet using spectral proper orthogonal decomposition (SPOD). Aerospace 5 (3), 73.CrossRefGoogle Scholar
Khorrami, M.R., Malik, M.R. & Ash, R.L. 1989 Application of spectral collocation techniques to the stability of swirling flows. J. Comput. Phys. 81 (1), 206–229.CrossRefGoogle Scholar
Lesshafft, L., Semeraro, O., Jaunet, V., Cavalieri, A.V.G. & Jordan, P. 2019 Resolvent-based modeling of coherent wave packets in a turbulent jet. Phys. Rev. Fluids 4 (6), 1–27.CrossRefGoogle Scholar
Lumley, J.L. 1967 The Strucure of Inhomogeneous Turbulent Flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. A.M. Yaglom & V.I. Tatarski), pp. 166–178. Publishing House Nauka.Google Scholar
McKeon, B.J. & Sharma, A.S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Michalke, A. 1964 On the inviscid instability of the hyperbolictangent velocity profile. J. Fluid Mech. 19, 543–556.CrossRefGoogle Scholar
Morra, P., Semeraro, O., Henningson, D.S. & Cossu, C. 2019 On the relevance of Reynolds stresses in resolvent analyses of turbulent wall-bounded flows. J. Fluid Mech. 867, 969–984.CrossRefGoogle Scholar
Mullyadzhanov, R., Yavorsky, N. & Oberleithner, K. 2019 Linear stability of Landau jet: non-parallel effects. J. Phys.: Conf. Ser. 1268, 012050.Google Scholar
Mullyadzhanov, R.I., Sandberg, R.D., Abdurakipov, S.S., George, W.K. & Hanjalić, K. 2018 Propagating helical waves as a building block of round turbulent jets. Phys. Rev. Fluids 3, 062601.CrossRefGoogle Scholar
Oberleithner, K., Paschereit, C.O. & Wygnanski, I. 2014 a On the impact of swirl on the growth of coherent structures. J. Fluid Mech. 741, 156–199.CrossRefGoogle Scholar
Oberleithner, K., Rukes, L. & Soria, J. 2014 b Mean flow stability analysis of oscillating jet experiments. J. Fluid Mech. 757, 1–32.CrossRefGoogle Scholar
Oberleithner, K., Sieber, M., Nayeri, C.N. & Paschereit, C.O. 2011 On the control of global modes in swirling jet experiments. J. Phys.: Conf. Ser. 318 (3), 032050.Google Scholar
Parker, K., von Ellenrieder, K.D. & Soria, J. 2005 Using stereo multigrid DPIV (SMDPIV) measurements to investigate the vortical skeleton behind a finite-span flapping wing. Exp. Fluids 39 (2), 281–298.CrossRefGoogle Scholar
Pickering, E.M., Rigas, G., Sipp, D., Schmidt, O.T. & Colonius, T. 2019 Eddy viscosity for resolvent-based jet noise models. In 25th AIAA/CEAS Aeroacoustics Conference. American Institute of Aeronautics and Astronautics.CrossRefGoogle Scholar
Rajaratnam, N. 1976 Turbulent Jets, Developments in Water Science, vol. 5. Elsevier.Google Scholar
Rodríguez, D., Cavalieri, A.V.G., Colonius, T. & Jordan, P. 2015 A study of linear wavepacket models for subsonic turbulent jets using local eigenmode decomposition of PIV data. Eur. J. Mech. B/Fluids 49, 308–321.CrossRefGoogle Scholar
Rukes, L., Paschereit Oliver, C. & Oberleithner, K. 2016 An assessment of turbulence models for linear hydrodynamic stability analysis of strongly swirling jets. Eur. J. Mech. B/Fluids 59, 205–218.CrossRefGoogle Scholar
Salwen, H. & Grosch, C.E. 1981 The continuous spectrum of the Orr–Sommerfeld equation. Part 2. Eigenfunction expansions. J. Fluid Mech. 104, 445–465.CrossRefGoogle Scholar
Sasaki, K., Cavalieri, A.V.G., Jordan, P., Schmidt, O.T., Colonius, T. & Brès, G.A. 2017 High-frequency wavepackets in turbulent jets. J. Fluid Mech. 830, R2.CrossRefGoogle Scholar
Schiavo, L.A.C.A., Wolf, W.R. & Azevedo, J.L.F. 2017 Turbulent kinetic energy budgets in wall bounded flows with pressure gradients and separation. Phys. Fluids 29 (11), 115108.CrossRefGoogle Scholar
Schmid, P.J. & Henningson, D.S. 2001 Stability and Transition in Shear Flows. Springer Press.CrossRefGoogle Scholar
Schmidt, O.T., Towne, A., Rigas, G., Colonius, T. & Brès, G.A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.CrossRefGoogle Scholar
Soloff, S.M., Adrian, R.J. & Liu, Z.-C. 1997 Distortion compensation for generalized stereoscopic particle image velocimetry. Meas. Sci. Technol. 8 (12), 1441–1454.CrossRefGoogle Scholar
Soria, J. 1996 An investigation of the near wake of a circular cylinder using a video-based digital cross-correlation particle image velocimetry technique. Exp. Therm. Fluid Sci. 12 (2), 221–233.CrossRefGoogle Scholar
Symon, S., Rosenberg, K., Dawson, S.T.M. & McKeon, B.J. 2018 Non-normality and classification of amplification mechanisms in stability and resolvent analysis. Phys. Rev. Fluids 3 (5), 1–33.CrossRefGoogle Scholar
Tammisola, O. & Juniper, M.P. 2016 Coherent structures in a swirl injector at $Re=4800$ by nonlinear simulations and linear global modes. J. Fluid Mech. 792, 620–657.CrossRefGoogle Scholar
Tissot, G., Lajús, F.C., Cavalieri, A.V.G. & Jordan, P. 2017 a Wave packets and Orr mechanism in turbulent jets. Phys. Rev. Fluids 2 (9), 093901.CrossRefGoogle Scholar
Tissot, G., Zhang, M., Lajús, F.C., Cavalieri, A.V.G. & Jordan, P. 2017 b Sensitivity of wavepackets in jets to nonlinear effects: the role of the critical layer. J. Fluid Mech. 811, 95–137.CrossRefGoogle Scholar
Towne, A., Schmidt, O.T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.CrossRefGoogle Scholar
Wänström, M. 2009 Spatial decompositions of a fully-developed turbulent round jet sampled with particle image velocimetry. Phd thesis, Chalmers University of Technology.Google Scholar
Wygnanski, I. & Fiedler, H. 1969 Some measurements in the self-preserving jet. J. Fluid Mech. 38 (3), 577.CrossRefGoogle Scholar