Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T09:20:24.822Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear iterative method for closed-loop control of quasiperiodic flows

Published online by Cambridge University Press:  08 April 2019

Colin Leclercq Open the ORCID record for Colin Leclercq [Opens in a new window] ,
Fabrice Demourant ,
Charles Poussot-Vassal Open the ORCID record for Charles Poussot-Vassal [Opens in a new window]  and
Denis Sipp Open the ORCID record for Denis Sipp [Opens in a new window]
Colin Leclercq*
Affiliation:
ONERA DAAA, 8 rue des Vertugadins, 92190 Meudon, France
Fabrice Demourant
Affiliation:
ONERA DTIS, 2 avenue Edouard Belin, 31055 Toulouse, France
Charles Poussot-Vassal
Affiliation:
ONERA DTIS, 2 avenue Edouard Belin, 31055 Toulouse, France
Denis Sipp
Affiliation:
ONERA DAAA, 8 rue des Vertugadins, 92190 Meudon, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work proposes a feedback-loop strategy to suppress intrinsic oscillations of resonating flows in the fully nonlinear regime. The frequency response of the flow is obtained from the resolvent operator about the mean flow, extending the framework initially introduced by McKeon & Sharma (J. Fluid Mech., vol. 658, 2010, pp. 336–382) to study receptivity mechanisms in turbulent flows. Using this linear time-invariant model of the nonlinear flow, modern control methods such as structured ${\mathcal{H}}_{\infty }$-synthesis can be used to design a controller. The approach is successful in damping self-sustained oscillations associated with specific eigenmodes of the mean-flow spectrum. Despite excellent performance, the linear controller is however unable to completely suppress flow oscillations, and the controlled flow is effectively attracted towards a new dynamical equilibrium. This new attractor is characterized by a different mean flow, which can in turn be used to design a second controller. The method can then be iterated on subsequent mean flows, until the coupled system eventually converges to the base flow. An intuitive parallel can be drawn with Newton’s iteration: at each step, a linearized model of the flow response to a perturbation of the input is sought, and a new linear controller is designed, aiming at further reducing the fluctuations. The method is illustrated on the well-known case of two-dimensional incompressible open-cavity flow at Reynolds number 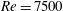$Re=7500$, where the fully developed flow is initially quasiperiodic (2-torus state). The base flow is reached after five iterations. The present work demonstrates that nonlinear control problems may be solved without resorting to nonlinear reduced-order models. It also shows that physically relevant linear models can be systematically derived for nonlinear flows, without resorting to black-box identification from input–output data; the key ingredient being frequency-domain models based on the linearized Navier–Stokes equations about the mean flow. Applicability to amplifier flows and turbulent dynamics has, however, yet to be investigated.

JFM classification

Flow Control: Instability control
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 26 - 65
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aleksić, K., Luchtenburg, M., King, R., Noack, B. & Pfeifer, J. 2010 Robust nonlinear control versus linear model predictive control of a bluff body wake. In 5th Flow Control Conference, p. 4833. AIAA.Google Scholar
Aleksić-Roessner, K., King, R., Lehmann, O., Tadmor, G. & Morzyński, M. 2014 On the need of nonlinear control for efficient model-based wake stabilization. Theor. Comput. Fluid Dyn. 28, 23–49.Google Scholar
Amestoy, P. R., Duff, I. S., Koster, J. & L’Excellent, J.-Y. 2001 A fully asynchronous multifrontal solver using distributed dynamic scheduling. SIAM J. Matrix Anal. Applics 23, 15–41.Google Scholar
Amestoy, P. R., Guermouche, A., L’Excellent, J.-Y. & Pralet, S. 2006 Hybrid scheduling for the parallel solution of linear systems. Parallel Comput. 32, 136–156.Google Scholar
Antoulas, A. C. 2005 Approximation of Large-Scale Dynamical Systems. SIAM.Google Scholar
Apkarian, P. & Noll, D. 2006 Nonsmooth H ∞ synthesis. IEEE Trans. Autom. Control 51 (1), 71–86.Google Scholar
Arbabi, H. & Mezić, I. 2017 Study of dynamics in post-transient flows using Koopman mode decomposition. Phys. Rev. Fluids 2, 124402.Google Scholar
Bagheri, S., Brandt, L. & Henningson, D. S. 2009 Input–output analysis, model reduction and control of the flat-plate boundary layer. J. Fluid Mech. 620, 263–298.Google Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2009 Closed-loop control of an open cavity flow using reduced-order models. J. Fluid Mech. 641, 1–50.Google Scholar
Barbagallo, A., Sipp, D. & Schmid, P. J. 2011 Input–output measures for model reduction and closed-loop control: application to global modes. J. Fluid Mech. 685, 23–53.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.Google Scholar
Bergmann, M., Cordier, L. & Brancher, J.-P. 2005 Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Phys. Fluids 17, 097101.Google Scholar
Blondel, V. & Tsitsiklis, J. N. 1997 NP-hardness of some linear control design problems. SIAM J. Control Optim. 35 (6), 2118–2127.Google Scholar
Brunton, S. L. & Noack, B. R. 2015 Closed-loop turbulence control: progress and challenges. Appl. Mech. Rev. 67, 050801.Google Scholar
Butler, K. M. & Farrell, B. F. 1993 Optimal perturbations and streak spacing in wall-bounded turbulent shear flow. Phys. Fluids A 5, 774–777.Google Scholar
Camarri, S., Fallenius, B. E. G. & Fransson, J. H. M. 2013 Stability analysis of experimental flow fields behind a porous cylinder for the investigation of the large-scale wake vortices. J. Fluid Mech. 715, 499–536.Google Scholar
Carini, M., Airiau, C., Debien, A., Léon, O. & Pralits, J. O. 2017 Global stability and control of the confined turbulent flow past a thick flat plate. Phys. Fluids 29, 024102.Google Scholar
Cattafesta, L. N. III, Shukla, D., Garg, S. & Ross, J. 1999 Development of an adaptive weapons-bay suppression system. In 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, p. 1901. AIAA.Google Scholar
Cattafesta, L. N. III, Song, Q., Williams, D. R., Rowley, C. W. & Alvi, F. S. 2008 Active control of flow-induced cavity oscillations. Prog. Aerosp. Sci. 44 (7–8), 479–502.Google Scholar
Cherubini, S., Robinet, J.-Ch. & De Palma, P. 2010 The effects of non-normality and nonlinearity of the Navier–Stokes operator on the dynamics of a large laminar separation bubble. Phys. Fluids 22, 014102.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large–scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.Google Scholar
Dahan, J. A., Morgans, A. S. & Lardeau, S. 2012 Feedback control for form-drag reduction on a bluff body with a blunt trailing edge. J. Fluid Mech. 704, 360–387.Google Scholar
Dalla Longa, L., Morgans, A. S. & Dahan, J. A. 2017 Reducing the pressure drag of a d-shaped bluff body using linear feedback control. Theor. Comput. Fluid Dyn. 1–11.Google Scholar
Dandois, J., Garnier, E. & Pamart, P.-Y. 2013 Narx modelling of unsteady separation control. Exp. Fluids 54, 1445.Google Scholar
Del Álamo, J. C. & Jimenez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Dergham, G., Sipp, D., Robinet, J.-C. & Barbagallo, A. 2011 Model reduction for fluids using frequential snapshots. Phys. Fluids 23, 064101.Google Scholar
Duriez, T., Parezanovic, V., Laurentie, J.-C., Fourment, C., Delville, J., Bonnet, J.-P., Cordier, L., Noack, B. R., Segond, M., Abel, M. W. et al. 2014 Closed-loop control of experimental shear flows using machine learning. In 7th AIAA Flow Control Conference, p. 2219.Google Scholar
Efe, M., Debiasi, M., Yan, P., Özbay, H. & Samimy, M. 2005 Control of subsonic cavity flows by neural networks-analytical models and experimental validation. In AIAA Paper, vol. 294, p. 2005.Google Scholar
Flinois, T. L. B. & Morgans, A. S. 2016 Feedback control of unstable flows: a direct modelling approach using the Eigensystem Realisation Algorithm. J. Fluid Mech. 793, 41–78.Google Scholar
Foures, D. P. G., Dovetta, N., Sipp, D. & Schmid, P. J. 2014 A data-assimilation method for Reynolds-averaged Navier–Stokes-driven mean flow reconstruction. J. Fluid Mech. 759, 404–431.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.Google Scholar
Gautier, N., Aider, J.-L., Duriez, T., Noack, B. R., Segond, M. & Abel, M. 2015 Closed-loop separation control using machine learning. J. Fluid Mech. 770, 442–457.Google Scholar
Gómez, F. & Blackburn, H. M. 2017 Data-driven approach to design of passive flow control strategies. Phys. Rev. Fluids 2, 021901.Google Scholar
Gómez, F., Blackburn, H. M., Rudman, M., Sharma, A. S. & McKeon, B. J. 2016 A reduced-order model of three-dimensional unsteady flow in a cavity based on the resolvent operator. J. Fluid Mech. 798, R2.Google Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Hammond, D. A. & Redekopp, L. G. 1997 Global dynamics of symmetric and asymmetric wakes. J. Fluid Mech. 331, 231.Google Scholar
Heins, P. H., Jones, B. Ll. & Sharma, A. S. 2016 Passivity-based output-feedback control of turbulent channel flow. Automatica 69, 348–355.Google Scholar
Henning, L. & King, R. 2007 Robust multivariable closed-loop control of a turbulent backward-facing step flow. J. Aircraft 44, 201–208.Google Scholar
Henning, L., Pastoor, M., King, R., Noack, B. R. & Tadmor, G. 2007 Feedback control applied to the bluff body wake. In Active Flow Control (ed. King, R.), pp. 369–390. Springer.Google Scholar
Hervé, A., Sipp, D., Schmid, P. J. & Samuelides, M. 2012 A physics-based approach to flow control using system identification. J. Fluid Mech. 702, 26–58.Google Scholar
Högberg, M., Bewley, T. R. & Henningson, D. S. 2003 Relaminarization of Re 𝜏 = 100 turbulence using gain scheduling and linear state-feedback control. Phys. Fluids 15, 3572–3575.Google Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2011 Feedback control of flow resonances using balanced reduced-order models. J. Sound Vib. 330, 1567–1581.Google Scholar
Illingworth, S. J., Morgans, A. S. & Rowley, C. W. 2012 Feedback control of cavity flow oscillations using simple linear models. J. Fluid Mech. 709, 223–248.Google Scholar
Jacobi, I. & McKeon, B. J. 2011 Dynamic roughness perturbation of a turbulent boundary layer. J. Fluid Mech. 688, 258–296.Google Scholar
Jeun, J., Nichols, J. W. & Jovanović, M. R. 2016 Input–output analysis of high-speed axisymmetric isothermal jet noise. Phys. Fluids 28, 047101.Google Scholar
Jones, B. Ll., Heins, P. H., Kerrigan, E. C., Morrison, J. F. & Sharma, A. S. 2015 Modelling for robust feedback control of fluid flows. J. Fluid Mech. 769, 687–722.Google Scholar
Juniper, M. P. 2012 Absolute and convective instability in gas turbine fuel injectors. In ASME Turbo Expo 2010: Turbine Technical Conference and Exposition, pp. 189–198.Google Scholar
Juniper, M. P. & Sujith, R. I. 2018 Sensitivity and nonlinearity in thermoacoustics. Annu. Rev. Fluid Mech. 50, 661–689.Google Scholar
Kaiser, E., Noack, B. R., Cordier, L., Spohn, A., Segond, M., Abel, M., Daviller, G., Östh, J., Krajnović, S. & Niven, R. K. 2014 Cluster-based reduced-order modelling of a mixing layer. J. Fluid Mech. 754, 365–414.Google Scholar
Kegerise, M., Cattafesta, L. N. III & Ha, C.-S. 2002 Adaptive identification and control of flow-induced cavity oscillations. In 1st Flow Control Conference, p. 3158.Google Scholar
Khalil, H. K. 2002 Nonlinear Systems, 3rd edn. Prentice-Hall.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.Google Scholar
King, R., Seibold, M., Lehmann, O., Noack, B. R., Morzyński, M. & Tadmor, G. 2005 Nonlinear Flow Control Based on a Low Dimensional Model of Fluid Flow, pp. 369–386. Springer.Google Scholar
Lee, C., Kim, J., Babcock, D. & Goodman, R. 1997 Application of neural networks to turbulence control for drag reduction. Phys. Fluids 9, 1740–1747.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C.1997 ARPACK users’ guide: solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2010 A numerical study of global frequency selection in the time-mean wake of a circular cylinder. J. Fluid Mech. 645, 435–446.Google Scholar
Li, J. & Morgans, A. S. 2016 Feedback control of combustion instabilities from within limit cycle oscillations using H ∞ -infinity loop-shaping and the 𝜈-gap metric. Proc. R. Soc. Lond. A 472, 20150821.Google Scholar
Liu, K., Jacques, R. N. & Miller, D. W. 1996 Frequency domain structural system identification by observability range space extraction. J. Dyn. Syst. Meas. Cont. 118, 211–220.Google Scholar
Liu, Q., Sun, Y., Cattafesta, L. N., Ukeiley, L. S. & Taira, K.2018 Resolvent analysis of compressible flow over a long rectangular cavity. AIAA Paper 2018-0588.Google Scholar
Loiseau, J.-Ch. & Brunton, S. L. 2018 Constrained sparse galerkin regression. J. Fluid Mech. 838, 42–67.Google Scholar
Luchtenburg, D. M., Aleksić, K., Schlegel, M., Noack, B. R., King, R., Tadmor, G., Günther, B. & Thiele, F. 2010 Turbulence control based on reduced-order models and nonlinear control design. In Active Flow Control II, pp. 341–356. Springer.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2014 Opposition control within the resolvent analysis framework. J. Fluid Mech. 749, 597–626.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2015 A framework for studying the effect of compliant surfaces on wall turbulence. J. Fluid Mech. 768, 415–441.Google Scholar
Mantič-Lugo, V. & Gallaire, F. 2016 Self-consistent model for the saturation mechanism of the response to harmonic forcing in the backward-facing step flow. J. Fluid Mech. 793, 777–797.Google Scholar
McKelvey, T., Akcay, H. & Ljung, L. 1996 Subspace-based multivariable system identification from frequency response data. IEEE Trans. Autom. Control 41, 960–979.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
McKeon, B. J., Sharma, A. S. & Jacobi, I. 2013 Experimental manipulation of wall turbulence: a systems approach. Phys. Fluids 25, 031301.Google Scholar
Meliga, P. 2017 Harmonics generation and the mechanics of saturation in flow over an open cavity: a second-order self-consistent description. J. Fluid Mech. 826, 503–521.Google Scholar
Meliga, P., Pujals, G. & Serre, E. 2012 Sensitivity of 2-d turbulent flow past a d-shaped cylinder using global stability. Phys. Fluids 24, 061701.Google Scholar
Mettot, C., Renac, F. & Sipp, D. 2014a Computation of eigenvalue sensitivity to base flow modifications in a discrete framework: application to open-loop control. J. Comput. Phys. 269, 234–258.Google Scholar
Mettot, C., Sipp, D. & Bézard, H. 2014b Quasi-laminar stability and sensitivity analyses for turbulent flows: prediction of low-frequency unsteadiness and passive control. Phys. Fluids 26, 061701.Google Scholar
Mezić, I. 2013 Analysis of fluid flows via spectral properties of the Koopman operator. Annu. Rev. Fluid Mech. 45, 357–378.Google Scholar
Mittal, S. 2007 Global linear stability analysis of time-averaged flows. Intl J. Numer. Meth. Fluids 58, 111.Google Scholar
Moarref, R, Jovanović, M. R., Tropp, J. A., Sharma, A. S. & McKeon, B. J. 2014 A low-order decomposition of turbulent channel flow via resolvent analysis and convex optimization. Phys. Fluids 26, 051701.Google Scholar
Nagarajan, K. K., Cordier, L. & Airiau, C. 2013 Development and application of a reduced order model for the control of self-sustained instabilities in cavity flows. Commun. Comput. Phys. 14, 186–218.Google Scholar
Nakashima, S., Fukagata, K. & Luhar, M. 2017 Assessment of suboptimal control for turbulent skin friction reduction via resolvent analysis. J. Fluid Mech. 828, 496–526.Google Scholar
Noack, B. R., Schlegel, M., Morzyński, M. & Tadmor, G. 2011 Galerkin method for nonlinear dynamics. In Reduced-Order Modelling for Flow Control, pp. 111–149. Springer.Google Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.Google Scholar
Pillarisetti, A. & Cattafesta, L. III 2001 Adaptive identification of fluid-dynamic systems. In 15th AIAA Computational Fluid Dynamics Conference, p. 2978.Google Scholar
Poussot-Vassal, C. & Sipp, D. 2015 Parametric reduced order dynamical model construction of a fluid flow control problem. IFAC-PapersOnLine 48, 133–138.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Rowley, C. W. & Dawson, S. T. M. 2017 Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 49, 387–417.Google Scholar
Rowley, C. W. & Williams, D. R. 2006 Dynamics and control of high-Reynolds-number flow over open cavities. Annu. Rev. Fluid Mech. 38, 251–276.Google Scholar
Rowley, C. W., Williams, D. R., Colonius, T., Murray, R. M. & Macmynowski, D. G. 2006 Linear models for control of cavity flow oscillations. J. Fluid Mech. 547, 317–330.Google Scholar
Samimy, M., Debiasi, M., Caraballo, E., Serrani, A., Yuan, X., Little, J. & Myatt, J. H. 2007 Feedback control of subsonic cavity flows using reduced-order models. J. Fluid Mech. 579, 315–346.Google Scholar
Sartor, F., Mettot, C., Bur, R. & Sipp, D. 2015a Unsteadiness in transonic shock-wave/boundary-layer interactions: experimental investigation and global stability analysis. J. Fluid Mech. 781, 550–557.Google Scholar
Sartor, F., Mettot, C. & Sipp, D. 2015b Stability, receptivity, and sensitivity analyses of buffeting transonic flow over a profile. AIAA J. 53, 1980–1993.Google Scholar
Schmid, P. J. & Sipp, D. 2016 Linear control of oscillator and amplifier flows. Phys. Rev. Fluids 1, 040501.Google Scholar
Schmidt, O. T., Towne, A., Colonius, T., Cavalieri, A. V. G., Jordan, P. & Brs, G. A. 2017 Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 825, 1153–1181.Google Scholar
Semeraro, O., Bagheri, S., Brandt, L. & Henningson, D. S. 2011 Feedback control of three-dimensional optimal disturbances using reduced-order models. J. Fluid Mech. 677, 63–102.Google Scholar
Semeraro, O., Lesshafft, L., Jaunet, V. & Jordan, P. 2016 Modeling of coherent structures in a turbulent jet as global linear instability wavepackets: theory and experiment. Intl J. Heat Fluid Flow 62, 24–32.Google Scholar
Semeraro, O., Lusseyran, F., Pastur, L. & Jordan, P. 2017 Qualitative dynamics of wave packets in turbulent jets. Phys. Rev. Fluids 2, 094605.Google Scholar
Sharma, A. S. 2009 Model reduction of turbulent fluid flows using the supply rate. Intl J. Bifurcation Chaos 19, 1267–1278.Google Scholar
Sharma, A. S. & McKeon, B. J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.Google Scholar
Sharma, A. S., Morrison, J. F., McKeon, B. J., Limebeer, D. J. N., Koberg, W. H. & Sherwin, S. J. 2011 Relaminarisation of Re 𝜏 = 100 channel flow with globally stabilising linear feedback control. Phys. Fluids 23, 125105.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Sipp, D. & Schmid, P. J. 2016 Linear closed-loop control of fluid instabilities and noise-induced perturbations: a review of approaches and tools. Appl. Mech. Rev. 68, 020801.Google Scholar
Symon, S., Dovetta, N., McKeon, B. J., Sipp, D. & Schmid, P. J. 2017 Data assimilation of mean velocity from 2d PIV measurements of flow over an idealized airfoil. Exp. Fluids 58, 61.Google Scholar
Tissot, G., Zhang, M., Lajús, F. C. Jr., Cavalieri, A. V. G. & Jordan, P. 2017 Sensitivity of wavepackets in jets to nonlinear effects: the role of the critical layer. J. Fluid Mech. 811, 95–137.Google Scholar
Towne, A., Schmidt, O. T. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.Google Scholar
Turton, S. E., Tuckerman, L. S. & Barkley, D. 2015 Prediction of frequencies in thermosolutal convection from mean flows. Phys. Rev. E 91, 043009.Google Scholar
Williams, D., Kerstens, W., Pfeiffer, J., King, R. & Colonius, T. 2010 Unsteady lift suppression with a robust closed loop controller. In Active Flow Control II, pp. 19–30. Springer.Google Scholar